Giải bài 3.57 tr 167 SBT Hình học 10
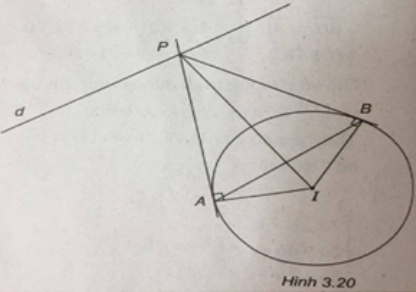
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x - 1)2 + (y + 2)2 = 9 và đường thẳng d: 3x - 4y + m = 0. Tìm m để trên d có duy nhất một điểm P mà từ đó có thể kẻ được hai tiếp tuyến PA, PB tới (C) (A, B là các tiếp điểm) sao cho tam giác PAB đều.
Hướng dẫn giải chi tiết
(C) có tâm I(1 ; -2) và bán kính R = 3. Ta có tam giác PAB đều thì IP = 2IA = 2R = 6 ⇔ P thuộc đường tròn (C’) có tâm I, bán kính R' = 6.
Trên d có duy nhất một điểm P thỏa mãn yêu cầu bài toán khi và chỉ khi d tiếp xúc với (C’) tại P
\( \Leftrightarrow d\left( {I,d} \right) = 6 \Leftrightarrow \frac{{\left| {3.1 - 4.\left( { - 2} \right) + m} \right|}}{5} = 6 \Leftrightarrow \left[ \begin{array}{l}
m = 19\\
m = - 41
\end{array} \right.\)
-- Mod Toán 10 HỌC247
-
Tìm tọa độ tâm đường tròn nội tiếp của tam giác DEF, biết rằng A có tung độ dương
bởi Bảo Lộc
08/02/2017
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC nội tiếp đường tròn tâm I(2;1), bán kính R = 5. Chân đường cao hạ từ B, C, A của tam giác ABC lần lượt là D(4;2), E(1;- 2) và F. Tìm tọa độ tâm đường tròn nội tiếp của tam giác DEF, biết rằng A có tung độ dương.
Theo dõi (0) 1 Trả lời -
Xác định tọa độ các đỉnh A, B, C, biết rằng đỉnh B thuộc đường thẳng \(\Delta : x - 2y + 4 = 0.\)
bởi hi hi
08/02/2017
Trong mặt phẳng với hệ tọa độ Oxy, cho hình thang vuông ABCD \((\widehat{BAD}=\widehat{ADC}=90^{0})\) có đỉnh D(2;2) và CD = 2AB. Gọi H là hình chiếu vuông góc của điểm D lên đường chéo AC. Điểm \(M(\frac{22}{5};\frac{14}{5})\) là trung điểm của HC. Xác định tọa độ các đỉnh A, B, C, biết rằng đỉnh B thuộc đường thẳng \(\Delta : x - 2y + 4 = 0.\)
Theo dõi (0) 1 Trả lời
