Bài tập 12 trang 119 SGK Hình học 10 NC

a) Ta có: \(a = 5,b = 3,c = \sqrt {{a^2} - {b^2}}  = 4\)

Tọa độ các tiêu điểm của (E) là F₁(−4;0), F₂(4;0)

Tọa độ các đỉnh của (E) là A₁(−5;0), A₂(5;0), B₁(0;−3), B₂(0;3)

b) (H) nhận (-4;0) và (4;0) làm đỉnh thì a = 4

(H) nhận (-5;0) và (5;0) làm tiêu điểm thì có c = 5

⇒ b² = c²−a² = 25−16 = 9 ⇒ b = 3

Vậy phương trình chính tắc của hypebol (H) là:

\(\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1\)

c) Vẽ (E) và (H).

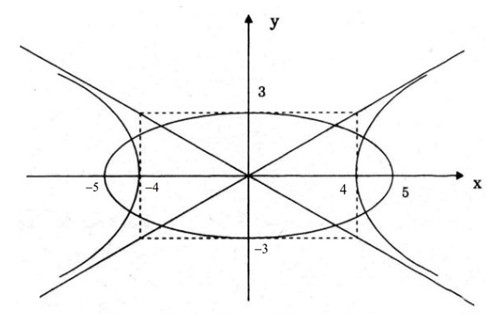
d) Tọa độ giao điểm của (E) và (H) là nghiệm của hệ phương trình:

\(\left\{ \begin{array}{l}
\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{9} = 1\\
\frac{{{x^2}}}{{16}} - \frac{{{y^2}}}{9} = 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{x^2} = \frac{{800}}{{41}}\\
{y^2} = \frac{{81}}{{41}}
\end{array} \right.\)

Vậy (E) và (H) cắt nhau tại 4 điểm có tọa độ thỏa phương trình \({x^2} + {y^2} = \frac{{881}}{{41}}\)

Vậy đường tròn đi qua các giao điểm của (E) và (H) có phương trình là \({x^2} + {y^2} = \frac{{881}}{{41}}\)

-- Mod Toán 10 HỌC247