Giải bài 3.61 tr 168 SBT Hình học 10
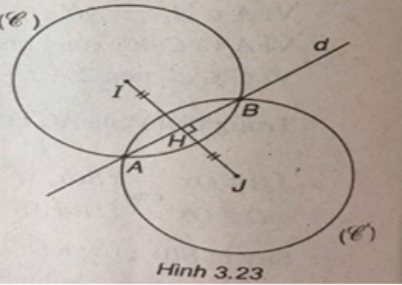
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x - 1)2 + (y - 2)2 = 4 và đường thẳng d: x - y - 1 = 0. Viết phương trình đường tròn (C ') đối xứng vơi đường tròng (C) qua đường thẳng d. Tìm tọa độ các giao điểm của (C) và (C').
Hướng dẫn giải chi tiết
Đường thẳng d có vectơ pháp tuyến là \(\overrightarrow n = \left( {1; - 1} \right)\). Do đó đường thẳng Δ đi qua tâm I(1; 2) và vuông góc với d có phương trình :
\(\frac{{x - 1}}{1} = \frac{{y - 2}}{{ - 1}} \Leftrightarrow x + y - 3 = 0\)
Tọa độ giao điểm H của d và là nghiệm của hệ phương trình :
\(\left\{ \begin{array}{l}
x - y - 1 = 0\\
x + y - 3 = 0
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = 2\\
y = 1
\end{array} \right. \Rightarrow H\left( {2;1} \right)\)
Gọi J là điểm đối xứng của I qua d. Khi đó :
\(\left\{ \begin{array}{l}
{x_J} = 2{x_H} - {x_I} = 3\\
{y_J} = 2{y_H} - {y_I} = 0
\end{array} \right. \Rightarrow J\left( {3;0} \right)\)
Vì (C') đối xứng với (C ) qua d nên (C') có tâm là J(3; 0) và bán kính R = 2.
Do đó (C') có phương trình là: (x - 3)2 + y2 = 4
Tọa độ các giao điểm của (C ) và (C') là nghiệm của hệ phương trình :
\(\begin{array}{l}
\left\{ \begin{array}{l}
{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 4\\
{\left( {x - 3} \right)^2} + {y^2} = 4
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x - y - 1 = 0\\
{\left( {x - 3} \right)^2} + {y^2} = 4
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
x = 1,y = 0\\
x = 3,y = 2
\end{array} \right.
\end{array}\)
Vậy tọa độ giao điểm của (C) và (C') là A(1; 0) và B(3; 2).
-- Mod Toán 10 HỌC247
-


Qua điểm E thuộc cạnh BC kẻ đường thẳng vuông góc với DE cắt đường thẳng AB tại F
bởi Thụy Mây
 07/02/2017
07/02/2017
Trong mặt phẳng với hệ tọa độ Oxy, cho hình thang vuông ABCD có \(\widehat{BCD}=\widehat{ADC}=90^0\), và BC = CD = \(\frac{1}{2}AD\). Qua điểm E thuộc cạnh BC kẻ đường thẳng vuông góc với DE cắt đường thẳng AB tại F. Tìm tọa độ các điểm B, C, D biết A(6;-2), E(1;2) và F(5;-1)
Theo dõi (0) 1 Trả lời -


Trong mặt phẳng với hệ tọa độ Oxy cho đường tròn (C) \(x^{2}+y^{2}=2x\). Tam giác ABC vuông tại A có AC là tiếp tuyến của đường tròn (C) tại A, chân đường cao từ A của tam giác ABC là điểm H (2; 0). Tìm tọa độ đỉnh B của tam giác biết B có tung độ dương và diện tích tam giác ABC là \(\frac{2}{\sqrt{3}}\)
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có A(1;5), đường phân giác trong của góc A có phương trình x - 1 = 0
bởi Hương Lan
 08/02/2017
08/02/2017
Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(1;5), đường phân giác trong của góc A có phương trình x - 1 = 0, tâm đường tròn ngoại tiếp tam giác ABC là \(I(-\frac{3}{2};0)\) và điểm M(10;2) thuộc đường thẳng BC. Tìm tọa độ đỉnh B và C.
Theo dõi (0) 1 Trả lời -


Trong mặt phẳng Oxy, cho hình vuông ABCD có M là trung điểm của AB, N là điểm trên cạnh AD sao cho AN = 2ND
bởi Hy Vũ
 08/02/2017
08/02/2017
Trong mặt phẳng Oxy, cho hình vuông ABCD có M là trung điểm của AB, N là điểm trên cạnh AD sao cho AN = 2ND. Giả sử đường thẳng CN có phương trình x + 2y - 11 = 0 và điểm M\((\frac{5}{2};\frac{1}{2}).\) Tìm tọa độ điểm C.
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 3 trang 118 SGK Hình học 10 NC
Bài tập 4 trang 118 SGK Hình học 10 NC
Bài tập 5 trang 118 SGK Hình học 10 NC
Bài tập 6 trang 119 SGK Hình học 10 NC
Bài tập 7 trang 119 SGK Hình học 10 NC
Bài tập 8 trang 119 SGK Hình học 10 NC
Bài tập 9 trang 119 SGK Hình học 10 NC
Bài tập 10 trang 119 SGK Hình học 10 NC
Bài tập 11 trang 119 SGK Hình học 10 NC
Bài tập 12 trang 119 SGK Hình học 10 NC
Bài tập 13 trang 120 SGK Hình học 10 NC
Bài tập 14 trang 120 SGK Hình học 10 NC
Bài tập 3.37 trang 164 SBT Hình học 10
Bài tập 3.38 trang 165 SBT Hình học 10
Bài tập 3.39 trang 165 SBT Hình học 10
Bài tập 3.40 trang 165 SBT Hình học 10
Bài tập 3.41 trang 165 SBT Hình học 10
Bài tập 3.42 trang 165 SBT Hình học 10
Bài tập 3.43 trang 165 SBT Hình học 10
Bài tập 3.44 trang 165 SBT Hình học 10
Bài tập 3.45 trang 165 SBT Hình học 10
Bài tập 3.46 trang 166 SBT Hình học 10
Bài tập 3.47 trang 166 SBT Hình học 10
Bài tập 3.48 trang 166 SBT Hình học 10
Bài tập 3.49 trang 166 SBT Hình học 10
Bài tập 3.50 trang 166 SBT Hình học 10
Bài tập 3.51 trang 166 SBT Hình học 10
Bài tập 3.52 trang 167 SBT Hình học 10
Bài tập 3.53 trang 167 SBT Hình học 10
Bài tập 3.54 trang 167 SBT Hình học 10
Bài tập 3.55 trang 167 SBT Hình học 10
Bài tập 3.56 trang 167 SBT Hình học 10
Bài tập 3.57 trang 167 SBT Hình học 10
Bài tập 3.58 trang 167 SBT Hình học 10
Bài tập 3.59 trang 167 SBT Hình học 10
Bài tập 3.60 trang 167 SBT Hình học 10
Bài tập 1 trang 120 SGK Hình học 10 NC
Bài tập 3.62 trang 168 SBT Hình học 10
Bài tập 2 trang 120 SGK Hình học 10 NC
Bài tập 3 trang 120 SGK Hình học 10 NC
Bài tập 3.63 trang 168 SBT Hình học 10
Bài tập 4 trang 120 SGK Hình học 10 NC
Bài tập 5 trang 120 SGK Hình học 10 NC
Bài tập 3.64 trang 168 SBT Hình học 10
Bài tập 3.65 trang 168 SBT Hình học 10
Bài tập 3.66 trang 168 SBT Hình học 10
Bài tập 3.67 trang 168 SBT Hình học 10
Bài tập 6 trang 121 SGK Hình học 10 NC
Bài tập 7 trang 121 SGK Hình học 10 NC
Bài tập 8 trang 121 SGK Hình học 10 NC
Bài tập 9 trang 121 SGK Hình học 10 NC
Bài tập 10 trang 121 SGK Hình học 10 NC
Bài tập 11 trang 121 SGK Hình học 10 NC
Bài tập 12 trang 121 SGK Hình học 10 NC
Bài tập 13 trang 122 SGK Hình học 10 NC
Bài tập 14 trang 122 SGK Hình học 10 NC
Bài tập 15 trang 122 SGK Hình học 10 NC
Bài tập 16 trang 122 SGK Hình học 10 NC
Bài tập 17 trang 122 SGK Hình học 10 NC
Bài tập 18 trang 123 SGK Hình học 10 NC
Bài tập 3.68 trang 169 SBT Hình học 10
Bài tập 19 trang 123 SGK Hình học 10 NC
Bài tập 3.69 trang 169 SBT Hình học 10
Bài tập 20 trang 123 SGK Hình học 10 NC
Bài tập 3.70 trang 169 SBT Hình học 10
Bài tập 21 trang 123 SBT Hình học 10
Bài tập 3.71 trang 169 SBT Hình học 10
Bài tập 22 trang 123 SGK Hình học 10 NC
Bài tập 3.72 trang 169 SBT Hình học 10
Bài tập 23 trang 123 SGK Hình học 10 NC
Bài tập 3.73 trang 169 SBT Hình học 10
Bài tập 24 trang 123 SGK Hình học 10 NC
Bài tập 3.74 trang 169 SBT Hình học 10
Bài tập 3.75 trang 169 SBT Hình học 10
Bài tập 3.76 trang 170 SBT Hình học 10
Bài tập 3.77 trang 170 SBT Hình học 10
Bài tập 3.78 trang 170 SBT Hình học 10
Bài tập 3.79 trang 170 SBT Hình học 10
Bài tập 3.80 trang 170 SBT Hình học 10
Bài tập 3.81 trang 170 SBT Hình học 10
Bài tập 3.82 trang 170 SBT Hình học 10
Bài tập 3.83 trang 170 SBT Hình học 10
Bài tập 3.84 trang 171 SBT Hình học 10
Bài tập 3.85 trang 171 SBT Hình học 10
Bài tập 3.86 trang 171 SBT Hình học 10
Bài tập 3.87 trang 171 SBT Hình học 10
Bài tập 3.88 trang 171 SBT Hình học 10
Bài tập 3.89 trang 171 SBT Hình học 10
Bài tập 3.90 trang 171 SBT Hình học 10
Bài tập 3.91 trang 171 SBT Hình học 10
Bài tập 3.92 trang 172 SBT Hình học 10
Bài tập 3.93 trang 172 SBT Hình học 10
Bài tập 1 trang 93 SGK Hình học 10
Bài tập 2 trang 93 SGK Hình học 10
Bài tập 3 trang 93 SGK Hình học 10
Bài tập 4 trang 93 SGK Hình học 10
Bài tập 5 trang 93 SGK Hình học 10
Bài tập 6 trang 93 SGK Hình học 10