Để học tốt bài Tập hợp, HỌC247 xin mời các em học sinh cùng tham khảo bài giảng dưới đây bao gồm các kiến thức được trình bày cụ thể và chi tiết, cùng với các dạng bài tập minh họa giúp các em dễ dàng nắm vững được trọng tâm bài học.
Tóm tắt lý thuyết
1.1. Nhắc lại về tập hợp
Ở cấp Trung học cơ sở, trong toán học, người ta dùng từ tập hợp để chỉ một nhóm đối tượng nào đó hoàn toàn xác định. Mỗi đối tượng trong nhóm gọi là một phần tử của tập hợp đó.
Ví dụ:
a) Các học sinh của lớp 10A tạo thành một tập hợp. Các học sinh nữ của lớp này cũng tạo thành một tập hợp.
b) Các nghiệm của phương trình x2 — 4= 0 tạo thành một tập hợp (gọi là tập nghiệm của phương trình x2 — 4= 0). Tập hợp này có hai phân tử là 2 và - 2.
Người ta thường kí hiệu tập hợp bằng các chữ cái in hoa A, B, C..... và kí hiệu phần tử của tập hợp bằng các chữ cái in thường a, b, c,...
Chú ý: Đôi khi, để ngắn gọn người ta dùng từ “tập” thay cho “tập hợp”.
Để chỉ a là một phần tử của tập hợp A, ta viết a \(\in\) A (đọc là “a thuộc A”). Đề chỉ a không là phần tử của tập hợp A, ta việt a \(\notin\) A (đọc là *a không thuộc A”).
*Cách xác định tập hợp
Xét tập hợp A các số tự nhiên chẫn nhỏ hơn 15. Ta có thể viết tập hợp A đưới dạng điệt kê các phẩn tử.
A = {0;2; 4; 6: 8; 10; 12; 14},
hoặc dưới dang chỉ ra tỉnh chất đặc trưng cho các phân tử:
A = {x | x \(\in\) N, x chẵn và x < 15}
Chú ý: Khi liệt kê các phần tử của tập hợp, ta có một số chủ ý sau đây:
a) Các phần tử có thể được viết theo thứ tự tùy ý. Chẳng hạn, đễ viết tập hợp A các nghiêm của phương trình x(x - 1) =0, ta có thể viết A = {0; 1} hoặc A= {1:0}.
b) Mỗi phân tử chỉ được liệt kề một lần. Chẳng hạn, nêu kí hiệu B là tập hợp các chữ cái tiếng Anh trong tử *mathematics” thì B = (m; a; t; h; e; i; c; s}
c) Nếu quy tắc xác định các phân tử đủ rõ thì người ta dùng "...” mà không nhất thiết viết ra tắt cả các phần tử của tập hợp. Chẳng hạn, tập hợp các số tự nhiên không quá 100 có thể được viết là {0; 1; 2; ...; 100}.
Ví dụ: Viết mỗi tập hợp sau đưới đạng thích hợp:
a) Tập hợp A các ước đường của 18;
b) Tập hợp B các nghiệm của phương trình x2 + 3x - 4 = 0;
c) Tập hợp C các số tự nhuên lẻ;
4) Tập hợp D các nghiệm của phương trình x + 3y = 1.
Giải
a) Số 18 cỏ các ước đương là 1; 2; 3; 6; 9; 18. Do đó A = (1; 2; 3; 6; 9; 18}
b) Giải phương trình x2 + 3x - 4 = 0 nhận được hai nghiệm 1 và - 4. Do đỏ B = {1, - 4}. Ta cũng có thể viết \(B = {\rm{\{ }}x \in R|{x^{2\;}} + 3x - 4 = 0{\rm{\} }}\)
c) Ta có thể viết đưởi dang liệt kê các phần tử: C= (1; 3; 5; 7;...}. Ta cũng có thể viết dười dạng chỉ ra tính chất đặc trưng cho các phần tử: C = {x | x \(\in\) N, x là số lẻ} hoặc C= (x \(\in\) N |x là số lẻ) hoặc C= {x | x=2n+ 1, x \(\in\) N).
d) Ta viết D = {(x, y) | x,y \(\in\) R, x + 3y = 1}.
Chú ý: Có những tập hợp, như A và B ở Ví dụ trên, ta có thể đếm hết các phân tử của chúng. Những tập hợp như vậy được g
Nếu E là tập hợp hữu hạn thì số phần tử của nó được kí hiệu là n(E). Chẳng hạn. trong Vi dụ trên, ta có: n(A) = 6 và n(B) = 2.
Đặc biệt, n(Ø) = 0.
1.2. Tập con và hai tập hợp bằng nhau
|
Cho hai tập hợp A và B. Nếu mọi phân tử của A đều là phân từ của B thì ta nói tập hợp A là rập con của tập hợp B và kí hiệu \(A \subset B\) (đọc là A chứa trong B), hoặc \(B \supset A\) (đọc là B chứa A) |
|---|
Nhận xét
* \(A \subset A\) và \(Ø \subset A\) với mọi tập hợp A.
* Nếu A không phải là tập con của B thì ta kí hiệu \(A \not\subset B\) (đọc là A không chứa trong B hoặc B không chứa A).
* Nếu \(A \subset B\) hoặc \(B \subset A\) thì ta nói A và B có quan hề bao hàm.
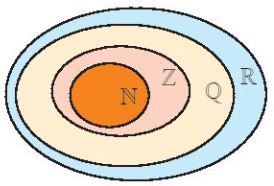
Chú ý: Giữa các tập hợp số quen thuộc (tập số tự nhiên, tập số nguyên, tập số hữu tỉ, tập số thực), ta có quan hệ bao hàm: \(N \subset Z \subset Q \subset R\)
Ví dụ: Trong mỗi trường hợp sau đây, các phần tử của tập hợp A có thuộc tập hợp B không? Hãy giải thích.
a) \(A = \{ - 1;1\} \) và \(B = \{ - 1;0;1;2\} \)
b) \(A = \mathbb{N}\) và \(B = \mathbb{Z}\)
c) A là tập hợp các học sinh nữ của lớp 10E, B là tập hợp các học sinh của lớp này.
d) A là tập hợp các loài động vật có vú, B là tập hợp các loài động vật có xương sống.
Giải
a) Có vì \( - 1 \in B,\;1 \in B\).
b) Có vì các số tự nhiên cũng là số nguyên.
c) Có vì các học sinh nữ của lớp 10E cũng là học sinh của lớp 10E.
d) Có vì các loài động vật có vú (còn gọi là thú) là một trong các lớp thuộc các loài động vật có xương sống.
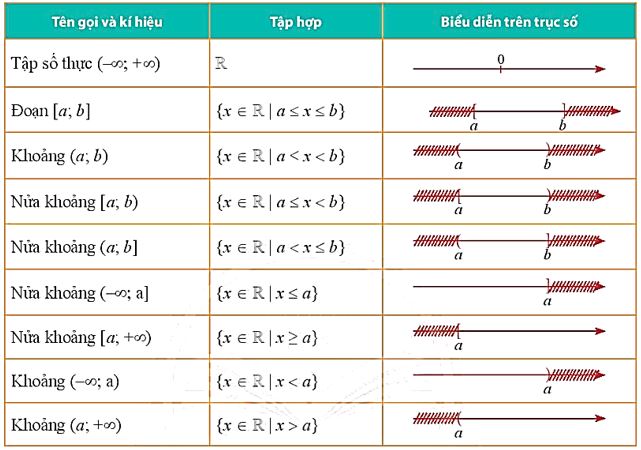
1.3. Một số tập con của tập hợp số thực
Sau này ta thường sử dụng các tập con của tập số thực sau đây (a và b là các số thực, a < b)
Bài tập minh họa
Câu 1: Viết tập hợp sau đây dưới dạng liệt kê các phần tử và tìm số phần tử của mỗi tập hợp đó:
a) Tập hợp A các ước của 24
b) Tập hợp B gồm các chữ số trong số 1113305;
c) \(C = \{ n \in \mathbb{N}|\;n\) là bội của 5 và \(n \le 30\} \)
d) \(D = \{ x \in \mathbb{R}|\;{x^2} - 2x + 3 = 0\} \)
Hướng dẫn giải
a) Số 24 có các ước là: \( - 24; - 12; - 8; - 6; - 4; - 3; - 2; - 1;1;2;3;4;6;8;12;24.\) Do đó \(A = \{ - 24; - 12; - 8; - 6; - 4; - 3; - 2; - 1;1;2;3;4;6;8;12;24\} \), \(n\;(A) = 16.\)
b) Số 1113305 gồm các chữ số: 1;3;0;5. Do đó \(B = \{ 1;3;0;5\} \), \(n\;(B) = 4.\)
c) Các số tự nhiên là bội của 5 và không vượt quá 30 là: 0; 5; 10; 15; 20; 25; 30. Do đó \(C = \{ 0;5;10;15;20;25;30\} \), \(n\,(C) = 7.\)
d) Phương trình \({x^2} - 2x + 3 = 0\) vô nghiệm, do đó \(D = \emptyset \), \(n\,(D) = 0.\)
Câu 2: Trong mỗi cặp tập hợp sau đây, tập hợp nào là tập con của tập hợp còn lại? Chúng có bằng nhau không?
a) \(A = \{ - \sqrt 3 ;\sqrt 3 \} \) và \(B = \{ x \in \mathbb{R}|{x^2} - 3 = 0\} \)
b) C là tập hợp các tam giác đều và D là tập hợp các tam giác cân;
c) \(E = \{ x \in \mathbb{N}|x\) là ước của 12\(\} \) và \(F = \{ x \in \mathbb{N}|x\) là ước của 24\(\} .\)
Viết tất cả các tập con của tập hợp \(A = \{ a;b\} .\)
Hướng dẫn giải
a) A là tập con củ B vì:
\( - \sqrt 3 \in \mathbb{R}\) thỏa mãn \({\left( { - \sqrt 3 } \right)^2} - 3 = 0\), nên \( - \sqrt 3 \in B\)
\(\sqrt 3 \in \mathbb{R}\) thỏa mãn \({\left( {\sqrt 3 } \right)^2} - 3 = 0\), nên \(\sqrt 3 \in B\)
Lại có: \({x^2} - 3 = 0 \Leftrightarrow x = \pm \sqrt 3 \) nên \(B = \{ - \sqrt 3 ;\sqrt 3 \} \).
Vậy A = B.
b) C là tập hợp con của D vì: Mỗi tam giác đều đều là một tam giác cân.
\(C \ne D\) vì có nhiều tam giác cân không là tam giác đều, chẳng hạn: tam giác vuông cân.
c) E là tập con của F vì \(24\; \vdots \;12\) nên các ước nguyên dương của 12 đều là ước nguyên dương của 24.
\(E \ne F\) vì \(24 \in F\)nhưng \(24 \notin E\)
Luyện tập Bài 2 Chương 1 Toán 10 CTST
Qua bài giảng Tập hợp này giúp các em nắm được các nội dung như sau:
- Sử dụng đúng các kí hiệu
- Biết cho tập hợp bằng cách liệt kê các phần tử của tập hợp hoặc chỉ ra tính chất đặc trưng của các phần tử của tập hợp.
- Vận dụng được các khái niệm tập hợp con, tập hợp bằng nhau vào giải bài tập.
3.1. Bài tập trắc nghiệm Bài 2 Chương 1 Toán 10 CTST
Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Toán 10 Chân trời sáng tạo Chương 1 Bài 2 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.
-
- A. 32
- B. 34
- C. 36
- D. 9
-
- A. ∅
- B. {a}
- C. {a;b}
- D. {∅;A} với A là một tập hợp khác rỗng
-
- A. 3
- B. 1
- C. Vô số
- D. 2
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
3.2. Bài tập SGK Bài 2 Chương 1 Toán 10 CTST
Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 10 Chân trời sáng tạo Chương 1 Bài 2 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Hoạt động khởi động trang 16 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 1 trang 16 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 2 trang 18 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 18 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá trang 18 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 4 trang 19 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 5 trang 19 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Vận dụng trang 20 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 6 trang 20 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 20 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 21 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 21 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 21 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 21 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 13 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 13 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 13 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 13 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 13 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 13 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 13 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 13 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 13 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 13 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Hỏi đáp Bài 2 Chương 1 Toán 10 CTST
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 10 HỌC247