Giải bài 3.40 tr 165 SBT Hình học 10
Trong mặt phẳng Oxy cho đường thẳng Δ: x - y + 2 = 0 và điểm A(2;0).
a) Chứng mình rằng hai điểm A và O nằm về cùng một phía đối với đường thẳng .
b) Tìm điểm M trên Δ sao cho độ dài đường gấp khúc OMA ngắn nhất.
Hướng dẫn giải chi tiết
a) Ta có:
Δ(O) = 2 > 0 ; Δ(A) = 2 + 2 > 0
Vậy A và O nằm về cùng một phía đối với Δ
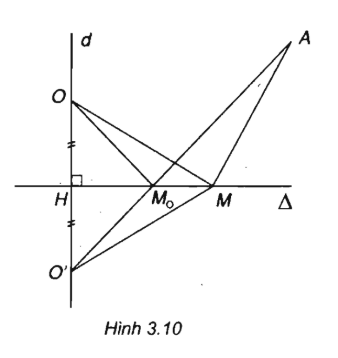
b) Gọi O' là điểm đối xứng của O qua Δ, ta có:
OM + MA = O'M + MA ≥ O'A
Ta có : OM + MA ngắn nhất ⇔ O', M, A thẳng hàng
Xét đường thẳng d đi qua O và vuông góc với Δ. Phương trình của d là: x + y = 0
d cắt Δ tại H(-1;1).
H là trung điểm của OO' suy ra O'(-2; 2)
Phương trình đường thẳng O'A là: x + 2y - 2 = 0
Giải hệ phương trình \(\left\{ \begin{array}{l}
x + 2y = 2\\
x - y = - 2
\end{array} \right.\)
Vậy ta được \(M\left( { - \frac{2}{3};\frac{4}{3}} \right)\)
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Bài tập 3 trang 118 SGK Hình học 10 NC
Bài tập 4 trang 118 SGK Hình học 10 NC
Bài tập 5 trang 118 SGK Hình học 10 NC
Bài tập 6 trang 119 SGK Hình học 10 NC
Bài tập 7 trang 119 SGK Hình học 10 NC
Bài tập 8 trang 119 SGK Hình học 10 NC
Bài tập 9 trang 119 SGK Hình học 10 NC
Bài tập 10 trang 119 SGK Hình học 10 NC
Bài tập 11 trang 119 SGK Hình học 10 NC
Bài tập 12 trang 119 SGK Hình học 10 NC
Bài tập 13 trang 120 SGK Hình học 10 NC
Bài tập 14 trang 120 SGK Hình học 10 NC
Bài tập 3.37 trang 164 SBT Hình học 10
Bài tập 3.38 trang 165 SBT Hình học 10
Bài tập 3.39 trang 165 SBT Hình học 10
Bài tập 3.41 trang 165 SBT Hình học 10
Bài tập 3.42 trang 165 SBT Hình học 10
Bài tập 3.43 trang 165 SBT Hình học 10
Bài tập 3.44 trang 165 SBT Hình học 10
Bài tập 3.45 trang 165 SBT Hình học 10
Bài tập 3.46 trang 166 SBT Hình học 10
Bài tập 3.47 trang 166 SBT Hình học 10
Bài tập 3.48 trang 166 SBT Hình học 10
Bài tập 3.49 trang 166 SBT Hình học 10
Bài tập 3.50 trang 166 SBT Hình học 10
Bài tập 3.51 trang 166 SBT Hình học 10
Bài tập 3.52 trang 167 SBT Hình học 10
Bài tập 3.53 trang 167 SBT Hình học 10
Bài tập 3.54 trang 167 SBT Hình học 10
Bài tập 3.55 trang 167 SBT Hình học 10
Bài tập 3.56 trang 167 SBT Hình học 10
Bài tập 3.57 trang 167 SBT Hình học 10
Bài tập 3.58 trang 167 SBT Hình học 10
Bài tập 3.59 trang 167 SBT Hình học 10
Bài tập 3.60 trang 167 SBT Hình học 10
Bài tập 3.61 trang 168 SBT Hình học 10
Bài tập 1 trang 120 SGK Hình học 10 NC
Bài tập 3.62 trang 168 SBT Hình học 10
Bài tập 2 trang 120 SGK Hình học 10 NC
Bài tập 3 trang 120 SGK Hình học 10 NC
Bài tập 3.63 trang 168 SBT Hình học 10
Bài tập 4 trang 120 SGK Hình học 10 NC
Bài tập 5 trang 120 SGK Hình học 10 NC
Bài tập 3.64 trang 168 SBT Hình học 10
Bài tập 3.65 trang 168 SBT Hình học 10
Bài tập 3.66 trang 168 SBT Hình học 10
Bài tập 3.67 trang 168 SBT Hình học 10
Bài tập 6 trang 121 SGK Hình học 10 NC
Bài tập 7 trang 121 SGK Hình học 10 NC
Bài tập 8 trang 121 SGK Hình học 10 NC
Bài tập 9 trang 121 SGK Hình học 10 NC
Bài tập 10 trang 121 SGK Hình học 10 NC
Bài tập 11 trang 121 SGK Hình học 10 NC
Bài tập 12 trang 121 SGK Hình học 10 NC
Bài tập 13 trang 122 SGK Hình học 10 NC
Bài tập 14 trang 122 SGK Hình học 10 NC
Bài tập 15 trang 122 SGK Hình học 10 NC
Bài tập 16 trang 122 SGK Hình học 10 NC
Bài tập 17 trang 122 SGK Hình học 10 NC
Bài tập 18 trang 123 SGK Hình học 10 NC
Bài tập 3.68 trang 169 SBT Hình học 10
Bài tập 19 trang 123 SGK Hình học 10 NC
Bài tập 3.69 trang 169 SBT Hình học 10
Bài tập 20 trang 123 SGK Hình học 10 NC
Bài tập 3.70 trang 169 SBT Hình học 10
Bài tập 21 trang 123 SBT Hình học 10
Bài tập 3.71 trang 169 SBT Hình học 10
Bài tập 22 trang 123 SGK Hình học 10 NC
Bài tập 3.72 trang 169 SBT Hình học 10
Bài tập 23 trang 123 SGK Hình học 10 NC
Bài tập 3.73 trang 169 SBT Hình học 10
Bài tập 24 trang 123 SGK Hình học 10 NC
Bài tập 3.74 trang 169 SBT Hình học 10
Bài tập 3.75 trang 169 SBT Hình học 10
Bài tập 3.76 trang 170 SBT Hình học 10
Bài tập 3.77 trang 170 SBT Hình học 10
Bài tập 3.78 trang 170 SBT Hình học 10
Bài tập 3.79 trang 170 SBT Hình học 10
Bài tập 3.80 trang 170 SBT Hình học 10
Bài tập 3.81 trang 170 SBT Hình học 10
Bài tập 3.82 trang 170 SBT Hình học 10
Bài tập 3.83 trang 170 SBT Hình học 10
Bài tập 3.84 trang 171 SBT Hình học 10
Bài tập 3.85 trang 171 SBT Hình học 10
Bài tập 3.86 trang 171 SBT Hình học 10
Bài tập 3.87 trang 171 SBT Hình học 10
Bài tập 3.88 trang 171 SBT Hình học 10
Bài tập 3.89 trang 171 SBT Hình học 10
Bài tập 3.90 trang 171 SBT Hình học 10
Bài tập 3.91 trang 171 SBT Hình học 10
Bài tập 3.92 trang 172 SBT Hình học 10
Bài tập 3.93 trang 172 SBT Hình học 10
Bài tập 1 trang 93 SGK Hình học 10
Bài tập 2 trang 93 SGK Hình học 10
Bài tập 3 trang 93 SGK Hình học 10
Bài tập 4 trang 93 SGK Hình học 10
Bài tập 5 trang 93 SGK Hình học 10
Bài tập 6 trang 93 SGK Hình học 10