Giải bài 94 tr 151 sách BT Toán lớp 7 Tập 1
Cho tam giác \(ABC\) cân tại \(A.\) Kẻ \(BD\) vuông góc với \(AC,\) kẻ \(CE\) vuông góc với \(AB.\) Gọi \(K\) là giao điểm của \(BD\) và \(CE.\) Chứng minh rằng \(AK\) là tia phân giác của góc \(A.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
- Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Lời giải chi tiết
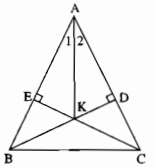
Xét hai tam giác vuông \(ADB\) và \(AEC\) có:
\(\widehat {A{\rm{D}}B} = \widehat {A{\rm{E}}C} = 90^\circ \)
\(AB = AC\) (vì tam giác \(ABC\) cân tại \(A\))
\(\widehat {A} \) chung
\( \Rightarrow ∆ADB = ∆AEC\) (cạnh huyền - góc nhọn).
\( \Rightarrow AD = AE\) (hai cạnh tương ứng).
Xét hai tam giác vuông \(ADK\) và \(AEK\) có:
\(\widehat {A{\rm{D}}K} = \widehat {A{\rm{E}}K} = 90^\circ \)
\(AD = AE\) (chứng minh trên)
\(AK\) cạnh chung
\( \Rightarrow ∆ADK = ∆AEK\) (cạnh huyền - cạnh góc vuông).
\( \Rightarrow \widehat {DAK} = \widehat {E{\rm{A}}K}\) (hai góc tương ứng).
Vậy \(AK\) là tia phân giác của góc \(BAC.\)
-- Mod Toán 7 HỌC247
-


Cho tam giác ABC vuông tại A. Kẻ đường phân giác BH, kẻ HM vuông góc với BC. Gọi N là giao điểm của AB và MH. Chứng minh
A, BH vuông góc AM
B, AM song song CN
Theo dõi (0) 1 Trả lời -


So sánh tam giác ADH và CEH biết tam giác ABC vuông cân tại A có AH vuông BC
bởi Vũ Hải Yến
 25/02/2019
25/02/2019
cho tam giác ABC vuông cân tại A có AH vuông góc với BC tại H. trên cạnh AB và AC lần lượt lấy các điểm D và E sao cho CE=AD.
định dạng các tam giác ABH và ACH
so sánh tam giác ADH với tam giác CEH
chứng minh rằng tam giác HDE là tam giác vuông cân
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC tại H.
a) Chứng minh rằng ΔAHB = ΔAHC.
b) Gọi I là trung điểm của cạnh AH. Trên tia đối của tia IB, lấy điểm D sao cho IB = ID. Chứng minh IB = IC, từ đó suy ra AH + BD > AB + AC.
c) Trên cạnh CI, lấy điểm E sao cho CI =2/3 CE . Chứng minh ba điểm D, E, H thẳng hàng.
Theo dõi (0) 1 Trả lời -


Cho ▲ABC ⊥ A. BD là tia phân giác góc B. Vẽ DI ⊥ BC, (điểm I thuộc BC. Gọi K là giao điểm hai đường thẳng DI và AB
a) Chứng minh: ▲ABD=▲IBD
b) Chứng minh: BD⊥AI
c) Chứng minh: DK=DC
d) Cho AB=6cm; AC=8cm. Hãy tính IC=?
Theo dõi (0) 1 Trả lời -


Cho Tam giác ABC , A = 90 độ ; có AB = AC . Qua A kẻ đường thẳng xy bất kỳ ( B và C nằm cùng phía với xy ) . Kẻ BM và CN cùng vuông góc với xy
a) Chứng minh tam giác BMA = tam giác ANC
b) Chứng minh BM + CN = MN
Ai làm Đ mik sẽ tick cho ng đó
Theo dõi (0) 1 Trả lời -


Tính BC của tam giác ABC có góc A=90 độ, AB=8cm, AC=6cm
bởi Kim Ngan
 25/02/2019
25/02/2019
Cho tam giác ABC có góc A=90 độ, AB=8 cm, AC= 6cm
a, Tính BC
b, Trên cạnh AC lấy điểm E sao cho AE= 2cm, trên tia đối của tia AB lấy điểm D sao cho AD= AB. Chứng minh tam giác BEC=DEC
c, Chứng minh DE đi qua trung điểm cạnh BC
Theo dõi (0) 1 Trả lời -


Cho ΔABC. M là trung điểm của BC. Vẽ BD ⊥ AM tại D, CE ⊥ AM tại E. Chứng minh rằng:
a) ΔDBM = ΔECM
b) BD = CE, DM = EM
c) AB + AC > 2AM
Nhanh lên nhé! Mk đang cần gấp
Theo dõi (0) 1 Trả lời -


1.
Cho tam giác ABC vuông cân tại A. Qua A kẻ đường xy không cắt cạnh BC. Từ B và C vẽ BM vuông góc xy, CE vuông góc với xy ( M,E thuộc xy ). CMR: ME=BM+CE
2.
Cho tam giác ABC cân tại A. Kẻ hai đường trung trực d1,d2 của hai cạnh AB, AC chúng cắt nhau tại O, M là trung điểm của BC, d1 cắt AB tại E, d2 cắt AC tại F
a) c/m: Tam giác AEO = tam giác AFO
b) c/m: A,O,M thẳng hàng
c) c/m: EF//BC
d) Tính cạnh bên của tam giác ABC biết AM = 4cm, BC = 6cm
3.
Cho tam giác ABC cân tại A. Trên tia đối của các tia BC, CB thứ tự lấy E,F sao cho BE = CF. Kẻ BH vuông góc AE tại H, kẻ CK vuông góc AF tại K. CMR:
a) BH = CK
b) BC//CK
Giúp mik với please
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có góc A = 90, AB<AC. Trên cạnh AC lấy điểm D sao cho AD=AB. Trên tia đối của AB lấy điểm E sao cho AE=AC
A, chứng minh DE=BC
B, chứng minh DE vuông BC
C, biết 4B =5C. Tính góc AED
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A , kẻ AH ⊥ BC . CM
a/ HB = HC
b/ Kẻ HM ⊥ AB , HN ⊥ AC cm tam giác HMB = tam giác HNC
c/ CM . tam giác AMN cân
Theo dõi (0) 1 Trả lời -


So sánh DA và DB biết CD là tia phân giác của góc ACB, DH vuông góc với BC tại H
bởi Dell dell
 28/02/2019
28/02/2019
Cho tam giác ABC vuông tại A , CD là tia phân giác của góc ACB , DH vuông góc với BC tại H , góc ABC bằng 300. DH cắt CA tại M .
a) So sánh DA và DB
b) Chứng minh Đ là trọng tâm của tam giác BCM
Ai làm được cho tick nha !!!!!!
Theo dõi (0) 1 Trả lời -


Tính độ dài DE theo BD và CE biết ABC cân có A=90 độ
bởi Lan Ha
 22/02/2019
22/02/2019
Cho tam giác cân ABC, Â = 90*. Qua a kẻ đường thẳng d. Từ B và C kẻ BD _|_ d, CE _|_ d. Tính độ dài DE theo BD và CE.
Theo dõi (0) 1 Trả lời -


Cm tam giác IOE=tam giác IOF biết E và F là chân đường vuông góc từ điểm I đến Ox, Oy
bởi Phạm Hoàng Thị Trà Giang
 22/02/2019
22/02/2019
1.Cho góc xOy < 180 độ và tia phân giác OM của góc đó. Trên tia OM lấy điểm I. Gọi E và F lần lượt là chân đường vuông góc kẻ từ điểm I đến Ox và Oy.
a) CM: △IOE = △IOF
b) CM: EF⊥OM
c) Tìm điều kiện của góc xOy để △OEF là △đều.
2. Cho O là điểm nằm giữa A và B của đoạn thẳng AB (O≠ A và B). Trên cùng một nửa mặt phẳng bờ AB vẽ các tia Ox, Oy sao cho góc AOx = góc BOy < 90 độ. Lấy điểm C ∈ tia Ox và điểm D ∈ tia Oy sao cho OC = OA và OD = OB. CMR : AD = BC.
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác KED=tam giác KEH biết EH=ED, đường thẳng qua H vuông EF
bởi Trần Thị Trang
 22/02/2019
22/02/2019
Cho tam giác DEF vuông tại D
a. Cho biết DE=6cm EF10cm Tính DF rồi so sánh các góccủa tam giác DEF
b. Trên EF, lấy H sao cho EH=ED. Từ H, vẽ đường thẳng vuông góc với EF cắt DF tại K. C/m tam giác KED= tam giác KEH
c. Trên tia đối của tia HK lấy M sao cho HM = HK. Chứng minh góc HFK= góc HFM
d. Từ H vẽ HP vuông góc FK; HQ vuông góc FM \(\left(P\in FK;Q\in FM\right)\)
Cho góc KFM = 60 độ và FH = 14cm. Tính PQ ( Làm tròn KQ đến chữ số thập phân thứ sáu)
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A.Kẻ AH ⊥ BC,HP ⊥ AB,HQ ⊥ AC.Trên tia đối của các tia PH cà QH lấy các điểm E và F sao cho PE=PH,QF=QH.Chứng minh
a)∆APE=∆APH
b)∆AQH=∆AQF
c)3 điểm E,A,F thẳng hàng
d)BE//CF
Theo dõi (0) 1 Trả lời -


Cho ∆ ABC vuông tại A, biết góc ABC = 60 độ và AB = 6cm Trên cạnh BC lấy điểm E sao cho BA=BE . Đường thẳng vuông góc với BC tại E cắt AC tại D
a, CM ∆ABD=∆EBD
b, CM ∆ ABE là tam giác đều và tính độ dài cạnh BC
c, Vẽ AH vuông góc với BC tại H. Tia phân giác của góc BAH cắt BC tại G. CM rằng CA= CG
mong các bạn giúp đỡ mik mai mik phải nộp rồi
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABH=tam giác ACH biết tam giác ABC cân tại A có AH vuông BC
bởi Phạm Khánh Linh
 01/03/2019
01/03/2019
Cho \(\Delta ABC\) cân tại A. Kẻ \(H\perp BC\).
a) Chứng minh: \(\Delta ABH=\Delta ACH\)
b) Kẻ \(M\perp AB\), \(N\perp AC\). Chứng minh \(\Delta AMN\) cânTheo dõi (0) 1 Trả lời -


Chứng minh A là trung điểm CI biết từ A và D kẻ đường vuông góc với BE cắt BC tại M và N
bởi Choco Choco
 01/03/2019
01/03/2019
cho \(\Delta\)ABC có góc A vuông, AB = AC. Trên các cạnh AB, AC lấy 2 điểm D và E sao cho AD = AD. Từ A và D kẻ đường vuông góc với BE cắt BC tại M và N. Tia ND cắt CA ở I . C/m:
a. \(\Delta\)AID = \(\Delta\)ABE
b. A là truung điểm của CITheo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A có AB=AC. Qua A kẻ đường thẳng xy sao cho B,C nằm cùng phía với xy. Kẻ BD và CE vuông góc với xy
a) Chứng minh: DE=BD+CE
b) Gọi M là trung điểm của BC. Lấy điểm N là một điểm trên đoạn thẳng MC. Ke BP và CQ vuông góc với tia AN. Chứng minh PQ=BP-CQ
Theo dõi (0) 1 Trả lời -


Chứng minh HM=HN biết tam giác ABC cân tại A, đường trưng tuyến AH
bởi Phạm Hoàng Thị Trà Giang
 01/03/2019
01/03/2019
Cho tam giác ABC cân tại A.Kẻ đường trưng tuyến AH. Từ H kẻ đường vuông góc với AB,AC cắt AB,AC tại M,N.
Chứng minh rằng:
a)HB=HC
b)HM=HN
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân (AB = AC, góc A tù) . Trên cạnh BC lấy điểm D, trên tia đối của CB lấy điểm E sao cho BD = CE . Trên tia đối của CA lấy điểm I sao cho CI = CA
Câu 1: Chứng minh
a) Tam giác ABD bằng tam giác ICE
b) AB+AC < AD+AE
Câu 2: Từ D và E kẻ các đường thẳng vuông góc với AB, AI theo thứ tự tại M và N . Chứng minh BM = CN.
Câu 3: Chứng minh rằng chu vi tam giác ABC nhỏ hơn chu vi tam giác AMN
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A (góc A<90 độ). Vẽ BH vuông góc với AC (H thuộc AC), CK vuông góc với AB (K thuộc AB)
a, chứng minh rằng AH=AK
b, Gọi I là giao điểm của BH và CK. Chứng minh rằng AI là tia phân giác của góc A
Theo dõi (0) 1 Trả lời -


Chứng minh MH=MK biết MH vuông góc AB, MK vuông góc AC
bởi hai trieu
 01/03/2019
01/03/2019
Cho tam giác ABC có AB=AC. Tia phân giác góc A cắt BC tại M.
a) Chứng minh AM là đường trung trực của BC
b) Từ M vẽ MH vuông góc AB, MK vuông góc AC. Chứng minh MH=MK
Theo dõi (0) 1 Trả lời -


Tam giác ABC vuông tại A biết góc ABC= 60 độ và AB= 6 cm. Trên cạnh BC lấy điểm E sao cho BA=BE. Đường thẳng vuông góc với BC tại E cắt AC tại D
a) CM: tam giác ABD= tam giác EBD
b) CM: tam giác ABE đều, tính BC
c) Vẽ AH vuông góc với BC (H thuộc BC). Tia phân giác của góc BAH cắt BC tại G
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác FPN vuông biết M,N lần lượt là trung điểm của DE, DF
bởi Nguyễn Trà Long
 25/03/2019
25/03/2019
cho tam giác DEF vuông tại D. Gọi M,N lần lượt là trung điểm của DE,DF. Trên tia MN lấy điểm P sao N là trung điểm MP . cm
a)ΔDMN=ΔFPN
b)ΔFPN vuông
c)EP=ME
d)MN=\(\dfrac{1}{2}\)EF
e)Cho MP=12,DM=\(\dfrac{3}{5}\)DE.Tính DE=DF
Theo dõi (0) 1 Trả lời -


Chứng minh AK//BC biết tam giác ABC có góc A=90 độ và M trung điểm của AC
bởi Nguyễn Hồng Tiến
 25/03/2019
25/03/2019
Cho \(\Delta ABC;\widehat{A}=\) 90 độ; M là trung điểm của AC. Trên tia đối của tia MB lấy điểm K sao cho MK = MB. C/minh:
a, \(\Delta ABM=\Delta CKM\)
b, \(KC\perp AC\)
c, \(AK//BC\)
Theo dõi (0) 1 Trả lời -


Chứng minh AI là tia phân giác của góc A biết các tia phân giác góc B và C cắt nhau tại I
bởi Nguyễn Vân
 25/02/2019
25/02/2019
Cho Tam giác ABC các tia phân giác của góc B và C cắt nhau tại I Chứng Minh AI là tia phân giác của góc A
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A đường cao AH.
a) Chứng minh rằng: HB=HC.
b) Kẻ HK⊥ AC tại K và HM⊥ AB tại M.
c) Chứng minh rằng: KM // BC
d) Cho AK=16 cm, KC=9 cm. Tính AH
Theo dõi (0) 1 Trả lời -


1. Cho góc xOy = 90 độ. Trên tia Ox lấy M và trên tia Oy lấy A sao cho OM=4cm, OA=3cm. Vẽ tam giác MAB vuông cân tại A nằm trong xOy. Kẻ BH vuông góc với Oy. Tính chu vi tam giác AMB
Giúp mik với mik tick cho
Theo dõi (0) 1 Trả lời -


cho tam giác ABC vông tại A có AB=3cm AC=4cm
a.tính BC
b.kẻ AH vông AB trên tia đối của tia HA lấy điểm D sao cho HA=HD Chứng minh tam giác AHC=tam giác DHC
c. Tính AH
Theo dõi (0) 1 Trả lời -


Chứng minh 3 điểm E, D, F thẳng hàng biết trên tia đối AB lấy điểm F sao cho AF=CE
bởi Kim Ngan
 25/03/2019
25/03/2019
Tam giac ABC vuong tai A, phan giac BD. Qua D ke d.thang vuong goc voi BC tai E.
a) CM: tam giac BAD = tam giac BED
b) BD la trung truc cua AE
c) AD <DC
d) tren tia doi AB lay diem F sao cho AF =CE. CM: ba diem E, D, F thang hang
Theo dõi (0) 1 Trả lời -


Chứng minh BD=CE biết tam giác ABC cân tại A, BD vuông góc AC, E vuông góc AB
bởi Anh Nguyễn
 25/02/2019
25/02/2019
cho △ ABC cân tại A . Kẻ BD vuông góc AC( D∈AC) và E vuông góc với AB ( E∈AB)
a, CM : BD=CE
b,CM: ΔAED cân
c, goi I la giao điểm ủa BD và CE . CM:AI là tia phan giác của ∠A và AI vuông góc vs BC
Theo dõi (0) 1 Trả lời -


Cho tam giac MNI vuong tai M. Biet MI =8cm , MN =6cm
a. Tinh do dai canh NI
b. Ve tia phan giac cua goc MIN cat MN tai D. Ke DE vuong goc voi NI ( E thuoc NI) . CM: DM=DE
c. 2 duong thang DE va MI cat nhau tai A. CM: AN // EM
Theo dõi (0) 1 Trả lời -


1. Cho tam giác ABC vuông cân tại A, M là trung điểm của BC
a) c/m: tam giác AMC vuông cân
b) Lấy điểm I trên đoạn MC, kẻ BH, CK cùng vuông góc với AI, c/m: Tam giác AHB= tam giác CKA
c) c/m: tam giác MHK vuông cân
Theo dõi (0) 1 Trả lời -


Cho ∆ABC cân tại A (A < 90độ). Kẻ BH vuông góc AC (H ∈ AC). Kẻ CK vuông góc AB (K ∈ AB).
a. Chứng minh : AH = AK
b. Gọi I là giao điểm của BH và CK. Chứng minh : ∆BIC cân
c. Chứng minh: KH//BC
d. Chứng minh : AI là tia phân giác A
e. Gọi M là trung điểm của BC. Chứng minh : A, I, M thẳng hàng
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A gọi H là trung điểm của cạnh BC
a) Chứng minh rằng tam giác ABH bằng tam giác ACH
b) Từ H kẻ HM vuông góc với AB (M thuộc AB)HN vuông góc với AC (N thuộc AC )Chứng minh AM = AN
c) Chứng minh rằng tam giác MNP là tam giác cân
d) chứng minh cho AH vuông góc với MN
Giúp mk nhoa. Cảm ơn nhìn
Theo dõi (0) 1 Trả lời -


cho góc nhọn xOy Oz là pg của góc xOy, M là 1 điểm bất kì thuộc Oz ( M k trùng vs C Qua M vẽ đg thẳng A vuông góc vs Ox tại A cắt oy tại C và vẽ đg thẳng B vuông góc Oy tại B cắt Ox tại D.cm tam giac AOM=tam giac BOM
ve hinh nha
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A.Kẻ BD vuông góc với AC,CE vuông góc với AB. BD cắt CE cắt nhau tại H
a)Tam giác ADB=tam giác ACE
b)Tam giác AHC cân
c)ED song song BC
d)AH cắt BC tại K, trên HK lất M sao cho K là trung điểm của HM.CM tam giác ACM vuông
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A . Kẻ AH vuông góc với BC tại H . Trên cạnh BC lấy điểm E sao cho BE = BA . Kẻ EK vuông góc với AC ( K nằm trên AC ) .
Chứng minh : AK = AH .
Theo dõi (0) 1 Trả lời -


Cho tam giac ABC nhon va AB<AC co duong cao AH . Keo dai AH
them 1 doan HD bang voi HA so sanh tam giac ABH tam giac giac BHD
so sanh tam giac ACH va CDH
Theo dõi (0) 1 Trả lời -


cho tam giác ABC có AB=AC=5cm; BC=8cm. Kẻ AH⊥BC( H∈BC)
a. CM: BH=HC và góc BAH = góc CAH
b. tính độ dài AH
c. Kẻ HD⊥AB(D thuộc AB); HE⊥AC( E=AC). CMR: tam giác HDE cânTheo dõi (0) 1 Trả lời -


cho tam giác cân ABC có AB=AC. trên tia đối của tia BA lấy điểm D, tia CA lấy điểm E sao cho BD=CE.
a. CM: DE song song với BC
b. Từ D kẻ DM⊥BC, từ E kẻ EN⊥BC. CM: DM=EN
c. Chứng minh △AMN là tam giác cân
d. Từ B và C kẻ các đường vuông góc với AM và AN và chúng cắt nhau tại I. CMR: AI là tia phân giác chung của 2 góc BAC và góc MACTheo dõi (0) 1 Trả lời -


Cho \(\widehat{xOy}=90^0.\)Lấy A ϵOx,BϵOy,Eϵtia đối của Ox và F thuộc Oy sao cho OE=OB,OF=OA
C/M:EF=AB và EF⊥AB
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A, vẽ AD vuông góc BC (D thuộc BC).
a) Chứng minh BD=CD.
b) Vẽ DH vuông góc AB tại H và DK vuông góc AC tại K. Chứng minh DH= DK
c) Chứng minh HK // BC
d) Cho AB = 10cm; BC = 12cm. Tính AD
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A gọi M là trung điểm của BC Trên tia đối của tia MA lấy điểm D sao cho M là trung điểm của AD
A) Chứng minh tam giác MAB bằng tam giác MDC
B) Chứng minh CD vuông góc AC
C) Gọi M là trung điểm của AC Chứng minh NB=ND
D) cho góc abc bằng 60 độ Chứng minh tam giác MAB đều tính AC biết AB = 8 cm
Theo dõi (0) 1 Trả lời -


So sánh BC với MH biết M là giao điểm của AB và HE
bởi Bình Nguyen
 26/03/2019
26/03/2019
Cho tam giác ABC vuông tại A , đường phân giác BE , Kẻ EH vuông góc với BC ( H thuộc BC ) , gọi M là giao điểm của AB và HE , chứng minh rằng :
a , Tam giác ABE = tam giác HBEb,So sánh BC với MH
Theo dõi (0) 1 Trả lời -


Chứng minh EB vuông góc EF biết đường thẳng vuông góc với AH tại D cắt AC tại F
bởi Tram Anh
 26/03/2019
26/03/2019
Cho tam giác ABC vuông tại A, đường cao AH, điểm D nằm giữa A và H. Trên tia đối của tia HA lấy điểm E sao cho HE =AD. Đường thẳng vuông góc với AH tại D cắt AC tại F. CMR : EB vuông góc EF
Theo dõi (0) 1 Trả lời -


Cho \(\Delta ABC\) \(BE\perp AB,BE=CF=8cm\), độ dài các cạnh BF và BC tỉ lệ vs 3 và 5
a) Cm △ABC cân
b) Tính BC
c) BE và CF xắt nhau tại O. Nối Ao vs EF. CM Ao là đc trung tực của EF
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A , kẻ AH vuông góc BC ( H thuộc BC)
a) CM góc BAH= góc CAH
b) cho AH=3cm , BC=8 cm , tính độ dài AC
c) kẻ HE vuông góc AB, HD vuông góc AC . CM AE=AD
Theo dõi (0) 1 Trả lời -


Chứng minh OE=OF=OI biết OF vuông góc với AC, OI vuông góc với BC
bởi Nguyễn Phương Khanh
 28/03/2019
28/03/2019
Cho tam giác ABC, đường phân giác của góc A cắt đường phân giác của góc B tại O. Từ O hạ OE vuông góc với AB ( E thuộc AB ), từ O hạ OF vuông góc với AC ( F thuộc AC ), từ O hạ OI vuông góc với BC ( I thuộc BC ). CMR: OE = OF = OI
Theo dõi (0) 1 Trả lời -


Gọi M là trung điểm của BC của \(\Delta ABC\). Kẻ \(BH\perp AM,CK\perp AM\). Chứng minh rằng:
a/ BH // CK.
b/ M là trung điểm của HK.
c/ HC // BK.Theo dõi (0) 1 Trả lời -


cho tam giác abc,ab=ac.điểm d thuộc cạnh bc,trên tia đối cảu tia cb lấy điểm e sao cho bd=ce.các đường thẳng vuông góc với bc kẻ d và e cắt ab,ac tại m,n.đường thẳng bc cắt mn tại i.CMR
a,dm=ne
b,im=in
Theo dõi (0) 1 Trả lời -


Chứng minh BH=CK biết BH vuông AM, CK vuông góc AN
bởi bala bala
 28/03/2019
28/03/2019
Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M (M khác B), trên tia đối của tia CB lấy điểm N sao cho BM = CN.
a/ Chứng minh rằng AM = AN
b/ Kẻ , kẻ .Chứng minh rằng BH = CK.
c/ Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì? Vì sao?
---GIÚP MÌNH VỚI NHA !
Theo dõi (0) 1 Trả lời -


Chứng minh MD=ME biết tam giác ABC có AB=AC, M là trung điểm BC, MD vuông AB
bởi Nguyễn Thanh Trà
 28/03/2019
28/03/2019
Cho \(\Delta ABC\); AB = AC, M là trung điểm BC. Kẻ \(MD\perp AB,ME\perp AC\). CMR:
a) MD = ME
b) DE // BC
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác AMD=tam giác BND biết tam giác DMN cân tại D, MA vuông DN
bởi Sasu ka
 25/02/2019
25/02/2019
Cho tam giác DMN cân tại D , kẻ MA ⊥ DN , NB ⊥ DM
a/ CM : tam giác AMD = tam giác BND
b/ CM : tam giác ANM = tam giác BMN
c/ Gọi I là giao điểm của AM và BN , CM : DI là tia phân giác của D
Theo dõi (0) 1 Trả lời -


Chứng minh AM=1/2BC biết trên tia AM lấy điểm N sao cho M là trung điểm của AN
bởi truc lam
 28/03/2019
28/03/2019
Cho tam giác ABC có góc A=90 độ, M là trung điểm của BC. Trên tia AM lấy điểm N sao cho M là trung điểm của AN. CM:
a, CN=AB, CN//AB
b, AM=1/2 BC
Các bạn chỉ cần giúp mk giải câu b thôi k cần vẽ hình vs giải câu a đâu. Cảm ơn các bạn nhiều!
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Cho \(\Delta ABC\perp A\). Gọi M là trung điểm của BC. CMR: \(AM=\dfrac{BC}{2}\)
Giúp nhé!
♌Sư tử ♌
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABC=tam giác EBF biết F là giao điểm của BA và ED
bởi Dương Minh Tuấn
 28/03/2019
28/03/2019
cho \(\Delta ABC\) ( \(\widehat{A}\)= 90 ) , phân giác của \(\widehat{B}\) cắt AC tại D
a) Biết \(\widehat{ACB}\)= 40 . \(\widehat{ABD}=?\)
b) Trên canh BC lấy điểm E sao cho BE =AB .CMR : DE\(\perp AB\)
c) Gọi F là giao điểm của BA và ED . CM : \(\Delta ABC=\Delta EBF\)
d) Vẽ CK \(\perp BD\)\(=\left\{K\right\}\). CM : K ,F,C thẳng hàng
e) CM : \(AE//FC\)
GIÚP ĐC CÂU NÀO THÌ GIÚP NHÉ
Theo dõi (0) 1 Trả lời -


cho tam giác ABC vuông tại A có đường cao AH. trên cạnh BC lấy điểm D sao cho BD = BA
a) Chứng minh rằng góc BAD = góc BDA
b) chúng minh AD là tia phân giác của HAC
c) vẽ DK vuông góc với AC. Chúng minh AK = AH
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 66 trang 137 SGK Toán 7 Tập 1
Bài tập 93 trang 151 SBT Toán 7 Tập 1
Bài tập 95 trang 151 SBT Toán 7 Tập 1
Bài tập 96 trang 151 SBT Toán 7 Tập 1
Bài tập 97 trang 151 SBT Toán 7 Tập 1
Bài tập 98 trang 151 SBT Toán 7 Tập 1
Bài tập 99 trang 151 SBT Toán 7 Tập 1








