Giải bài 96 tr 151 sách BT Toán lớp 7 Tập 1
Cho tam giác \(ABC\) cân tại \(A.\) Các đường trung trực của \(AB, AC\) cắt nhau ở \(I.\) Chứng minh rằng \(AI\) là tia phân giác của góc \(A.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Lời giải chi tiết
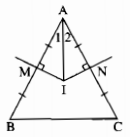
Gọi \(M,N\) lần lượt là trung điểm của \(AB\) và \(AC.\)
Suy ra \(IM, IN\) là hai đường trung trực của \(AB, AC.\)
Ta có:
\( AB{\rm{ }} = {\rm{ }}AC\) (vì \(\Delta ABC\) cân tại \(A\)) (1)
\(\displaystyle AM = {1 \over 2}AB\) (vì \(M\) là trung điểm của \(AB\)) (2)
\( \displaystyle AN = {1 \over 2}AC\) (vì \(N\) là trung điểm của \(AC\)) (3)
Từ (1), (2) và (3) suy ra: \(AM = AN\).
Xét hai tam giác vuông \(AMI\) và \(ANI\) có:
\(\widehat {AMI} = \widehat {ANI} = 90^\circ \)
\(AM = AN \) (chứng minh trên)
\(AI\) cạnh chung
\( \Rightarrow ∆AMI = ∆ANI\) (cạnh huyền - cạnh góc vuông).
\( \Rightarrow \widehat {{A_1}} = \widehat {{A_2}}\) (hai góc tương ứng).
Vậy \(AI\) là tia phân giác của \(\widehat {BAC}\).
-- Mod Toán 7 HỌC247
-


Cho XOY nhọn , OF là tia phân giác của góc đó . Qua điểm A thuộc Ox kẻ đường thẳng song song với OY cắt OZ ở N
Qua M kẻ đường thẳng song song với Ox cắt OY ở B
Chứng minh :
a, OA = OB ; MA = MB
b, Từ M kẻ MH vuông góc với Ox ; MK vuông góc với OY . Chứng minh MH = MK
Theo dõi (0) 1 Trả lời -


cho tam giác ABC vuông cân ở A.M là trung điểm của BC .Điểm E nằm giữa M và C .Kẻ BH,CK vuông góc với AE lần lượt tại H và K.Chứng minh rằng
a) BH=AK
b)tam giác MBH=tam giac MAK
c) tam giác MHA vuông cân
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có góc B = góc C và M là trung điểm của BC . Vẽ MH vuông góc AB , MK vuông góc với AC. CM
AH=AK
Theo dõi (0) 1 Trả lời -


Chứng minh ME=MF, BE=CF biết từ B và C kẻ các đường thẳng BE, CE vuông góc AM
bởi hành thư
 06/04/2019
06/04/2019
1. Cho ΔABC. Gọi M là trung điểm của BC. Từ B và C kẻ các đường thẳng BE và CE vuông góc với AM. CMR: ME=MF
BE=CF
Help me!
Theo dõi (0) 1 Trả lời -


Chứng minh AB^2+CH^2=AC^2+BH^2 biết tam giác ABC vuông tại A có AH vuông BC
bởi Tran Chau
 06/04/2019
06/04/2019
Cho tg ABC vuông tại A.Kẻ AH vuông góc BC tại H
a.CM:AB^2+CH^2=AC^2+BH^2
b.Trên AB lấy E,AC lấy F.CM:EF<BC
c.Biết AB=6 AC=8 Tính AH BH HC
Theo dõi (0) 1 Trả lời -


Chứng minh I là trung điểm BC biết tam giác ABC vuông cân tại A có AI vuông BC
bởi truc lam
 06/04/2019
06/04/2019
Tgiac ABC vuông cân tại A, kẻ AI vuông BC
A. Cm: I là trung điểm BC
B. Tgiac ABI, AIC là tgiac gì? Vì sao
Theo dõi (0) 1 Trả lời -


Tam giác BCD có gì đặc biệt biết tam giác ABC có A=90 độ và AC=4cm, C=60 độ?
bởi Nguyễn Hoài Thương
 25/02/2019
25/02/2019
vẽ một tam giác vuông ABC có góc A=90 AC=4cm góc C=60 trên tia đối cảu tia AC lấy điểm D sao cho AD=AC
a) chứng minh tam giác ABC= tam giác ABD
b) tam giác BCD có gì đặc biệt? vì sao?
c) tính độ dài các đoạn thẳng BC,ABTheo dõi (0) 1 Trả lời -


ΔABC⊥tại A. Đường thẳng AH⊥BC tại H. Vẽ các điểm I và K sao cho AB là đường trung trực của đoạn HI, và AC là đường trung trực của đoạn thẳng HK
a) Chứng minh AI=AK
b) Chứng minh 3 điểm I, K, A thẳng hàng
c) Biết góc CAH=30độ. Tính độ lớn góc ABC
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A, AB=AC. Qua A kẻ đường thẳng d bất kì không cắt cạnh nào của tam giác. Từ B và C ta kẻ BD⊥ d, CE⊥d.
a) chứng minh: ΔADB = ΔCEA.
b)chứng minh: BD+CE=DE.
c) Giả sử AC=2CE. Tính góc ECB và góc CBD.
d)Xét trường hợp đường thẳng d cắt cạnh BC tại một điểm. Tìm mỗi liên hệ giữa các đoạn thẳng: BD, EC và DE.
e) chứng minh: tổng BD2+CE2 có giá trị không đổi.
bn nào giải giúp mk vs ạ. mk tick cho. Cảm ơn nhiều
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác AME=DME biết tam giác ABC có AB=AC, D là trung điểm BC
bởi thùy trang
 08/04/2019
08/04/2019
Chi tam giac ABC co AB=AC goi D la trung duem cua BC E la trung Dien cua AD qua E ve duong thang vuong hoc voi AD cat AB tai M
CMR:a/ tam giac ABD= tam giac ACD
b/AD vuong goc BC
c/tam giac AME=tam giac DME
Theo dõi (0) 1 Trả lời -


Cho ΔABC có AB = AC tia phân giác góc A cắt BC tại D
1) CM ΔADB =ΔADC
2) vẽ DH ⊥ AB (H ϵ AB ), DK⊥ AC (Kϵ AC ) CMR DH=DK
3) Biết góc A = 4B . Tính các góc của tam giác ABC
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông cân tai A. Gọi D là 1 điểm thuộc AB. Trên tia đối của tia AC lấy điểm E. Sao cho AE=AD. Chứng mình rắng CD vuông góc với BE
Theo dõi (0) 1 Trả lời -


cho tam giác ABC có CA=CB=10cm ; AB=12cm , kẻ CI vuông góc với AB tại I
a)chứng minh IA =IB
b)kẻ IH vuông góc với AC tại H ; IK vuông góc với BC tại K ;so sánh IH và IK
bạn nào biết làm bài này thì giúp mình với
Theo dõi (0) 1 Trả lời -


Chứng minh AK là tia phân giác góc A biết tam giác ABC cân tại A và BD vuông AC
bởi Nguyễn Quang Thanh Tú
 25/02/2019
25/02/2019
Cho tam giác ABC cân tại A, \(\widehat{A}\) <90độ. Kẻ BD vuông góc với AC, kẻ CE vuông góc với AB. Gọi K là giao điểm của BD và CE. Chứng minh rằng AK là tia phân giác của góc A.
Theo dõi (0) 1 Trả lời -


Bài 1: Cho tam giác ABC vuông cân tại A. D ∈BC. Vẽ BE _|_ AD. CF _|_ AD. C/m AE = CF
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A có AB = 6, Ac = 8. Gọi E là trung điểm của AC, tia phân giác góc A cắt BC tại D
a) Tính BC b) Chứng minh tam giác BAD = tam giác EAD c) Chứng minh tam giác MAC vuông cân d) So sánh ME và MC e) D là giao điểm của các đường gì trong tam giác AMC f) Chứng minh DC = 2BD g) Tính BD và DCTheo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A, BD là phân giác của góc B. Vẽ DI vuông góc với BC (điểm I thuộc BC). Gọi K là giao điểm của 2 đường thẳng DI và AB.
a) Chứng minh tam giác ABD = tam giác IBD
b) Chứng minh BD vuông góc AI
c) Chứng minh DK = DCd) Cho AB = 6cm ; AC = 8cm. Hãy tính IC =?
Theo dõi (0) 1 Trả lời -


cho góc xOy khác góc bẹt. Vẽ tia phân giác Ot của góc xOy. Trên Ot lấy điểm M, đường thẳng d đi qua M và vuông góc với Ot cắt Ox, Oy theo thứ tự A và B. CMR:
a) OA=OB
b) lấy C thuộc Ot. CMR: CA=CB và góc dAC= góc dBC
 mn nhanh giúp mình nhaTheo dõi (0) 1 Trả lời
mn nhanh giúp mình nhaTheo dõi (0) 1 Trả lời -


Cho tam giác ABC có A=80 độ, B=70 độ. Tính C bằng cách qua C kẻ đường thẳng song song với AB.
Theo dõi (0) 1 Trả lời -


Chứng minh góc DBK=45 độ biết tam giác ABC vuông tại A có tia phân giác góc B cắt AC
bởi Sasu ka
 08/04/2019
08/04/2019
Cho tam giác ABC vuông tại A(AB>AC). Tia phân giác góc B cắt AC tại D. Kẻ DH vuông góc BC. Trên tia AC lấy điểm E sao cho AE=AB. Đường thẳng vuông góc AE tại E cắt tia DA ở K. CMR: a, BA=BH
b, Góc DBK =45o
Theo dõi (0) 1 Trả lời -


Cho ΔABC có AB=AC , kẻ BD⊥AC tại D, CE ⊥AB tại E
a)CMR ΔABD=ΔACE
b)CMR BD=CE
c)Gọi O là giao điểm của BD và CE . CMR ΔOEB=ΔODC
d)CMR AO là tia phân giác \(\widehat{BAC}\)
Theo dõi (0) 1 Trả lời -


Chứng minh DH+DK=BM biết tam giác ABC có góc A=góc C, DH vuông góc AB, DK vuông góc AC
bởi Nguyễn Xuân Ngạn
 09/04/2019
09/04/2019
Cho \(\Delta ABC\) có \(\widehat{B}=\widehat{C}\) , trên cạnh BC lấy điểm D kẻ \(DH\perp AB,DK\perp AC,BM\perp AC\) . Chứng minh DH+DK=BM
Theo dõi (0) 1 Trả lời -


Cho ΔABC vuông tại A. Trên tia đối của tia AC lấy điểm D sao cho AD = AC.
C/m: a, ΔABC = ΔABD
b, Trên tia AD lấy điểm M. Chứng minh ΔMBD = ΔMBC
Theo dõi (0) 1 Trả lời -


Cho \(\Delta\)ABC vuông tại A. Vẽ đường cao AH. Trên cạnh BC lấy điểm D sao cho BD=BA.
a. Chứng minh góc BAD= góc ADB
b. Chứng minh AD là tia phân giác của góc HAC
c. Vẽ DK\(\perp\)AC ( K\(\in\)AC). Chứng minh AK=AH
Theo dõi (0) 1 Trả lời -


cho tam giác ABC vuông tại A có AB=AC . Qua A kẻ đường thẳng xy(BC nằm cùng phía đối với xy ) . Chứng minh
a) tam giác BAD=tam giác CAE
b) DE=BD+CE
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A, Gọi M là trung diểm của cạnh Bc
a) chứng minh: Δ ABM = ΔACM
b) từ M vẽ MH vuông góc với AB và MK vuông góc với AC. chứng minh BH=CK
c) Từ B vẽ BP vuông góc với AC, BP cắt MH tại I. chứng minh ΔIBM cân
Theo dõi (0) 1 Trả lời -


Chứng minh HK=BH+CK biết tam giác ABC vuông tại A có AB=AC, BH và CK vuông góc với d
bởi thu thủy
 08/04/2019
08/04/2019
Cho ΔABC vuông tại A, AB = Ac. Qua A vẽ đường thẳng d sao cho B và C nằm cùng phía đối với đường thẳng d. Kẻ Bh và CK vuông góc với d. Chứng minh:
a) AH = CK
b) HK = BH + CK
Theo dõi (0) 1 Trả lời -


Chứng minh DE//BC biết tam giác ABC cân tại A có các đường phân giác BD, CE
bởi Duy Quang
 25/02/2019
25/02/2019
Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D thuộc AC, E thuộc AB). Chứng minh rằng DE // BC.
(Vẽ hơi dở, thông cảm ! Mà các bn chỉ cần giải dùm mình bài này là được ồi. Thanks nếu bn trả lời câu hỏi này. Ok ???)
Theo dõi (0) 1 Trả lời -


Tam giác MHK có điểm gì đặc biệt biết tam giác ABC vuông tại A, M là trung điểm BC?
bởi Nguyễn Minh Hải
 25/02/2019
25/02/2019
Cho tam giác ABC vuông tại A . Gọi M là trung điểm BC , E là điểm nằm giữa B và C nhưng không trùng vói M . Kẻ Bh , CK vuông góc với AE( H và K thuộc AE) . Tam giác MHK có điểm gì đặc biệt ? Vì sao ?
Làm ơn giúp mk với !!!!!!!!
Đi mà !!!!!!
Theo dõi (0) 1 Trả lời -


Tính góc BAC biết tam giác ABC nhọn, AD vuông góc với BC, BE vuông góc AC
bởi Nguyễn Tiểu Ly
 09/04/2019
09/04/2019
Cho tam giác ABC nhọn. kẻ AD vuông góc với BC( D thuộc BC); kẻ BE vuông góc với AC( E thuộc AC). AD cắt BE tại H. Biết AH=BC. Tính \(\widehat{BAC}\)
Theo dõi (0) 1 Trả lời -


Chứng minh DE=DA biết tam giác ABC vuông tại A có phân giác BD, DE vuông góc BC
bởi Lê Minh Trí
 09/04/2019
09/04/2019
cho tam giác ABC vuong tại A , phân giác BD kẻ DE vuong góc với BC , K là giao điểm của hai đuong thẳng AB và DE.
chứng minh : A) DE=DA
B) BC=DK
C) gọi I là giao điểm của CK . chứng minh BDI thẳng hàng
Theo dõi (0) 1 Trả lời -


cho tam giác ABC vuông tại A.Kẻ BD là phân giác của góc B.Kẻ AI vuông góc BD tại I.AI cắt BC tại E
a) chứng minh AB=EB
b) chứng minh tam giác BED vuông
c) DE cắt AB tại F, chứng minh AE//FC
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có AB=AC, M là tr/điểm của BC, từ M kẻ MH⊥AB, AC⊥MK( H thuộc AB, K thuộc AC). Cminh:
a)AM ⊥BC
b)AH=AK
c)HK//BC
Theo dõi (0) 1 Trả lời -


Chứng minh DK=DC biết tam giác ABC vuông tại A, K là giao điểm của DI và AB
bởi Trần Phương Khanh
 09/04/2019
09/04/2019
Cho △ ABC vuông tại A. Tia phân giác của góc ABC cắt AC tại D. Kẻ DI vuông góc với BC (I ∈ BC )
a)Chứng minh △ABD=△IBD
b) Chứng minh BD ⊥AI
c)Gọi K là giao điểm của hai đường thẳng DI và AB. Chứng minh DK = DC
d)Từ I kẻ đường thẳng // với BD cắt AB tại E. Chứng minh △ BIE cân
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A. Trung trực của AB và AC cắt nhau tại O . Gọi I và J là các điểm nằm trên 2 cạnh AB và AC sao cho AI = CJ biết góc BAC = 30 độ . Tính số đo góc IOJ ?
Theo dõi (0) 1 Trả lời -


Chứng minh DI=IE biết ở ngoài tam giác ABC vẽ các tam giác vuông tại A là ABD, ACE
bởi Phạm Hoàng Thị Trà Giang
 09/04/2019
09/04/2019
Cho Δ ABC . Ở phía ngoài Δ ABC vẽ các tam giác vuông tại A đó là Δ ABD và Δ ACE có AB = AD và AC = AE Kẻ AH⊥ BC. Gọi I là giao điểm HA và DE . Chứng minh: DI = IE
Giúp mk ik!!!!!Mai phải nộp r!!!
Mk cần gấp!!!????
Theo dõi (0) 1 Trả lời -


cho tam giác ABC Cân tại A ( góc A khác 120 độ ) vẽ ra phía ngoài tam giác các tam giác đều ABD và ACE. Gọi O là giao điểm của BE và CD. chứng minh
a/ BE = CE
b/ OB = OC
c/ D và E cách đều đường thẳng BC
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có góc A=90 độ và AB=AC. Trên cạnh AB, AC lấy hai điểm D và E sao cho AD=AE. Từ A và D kẻ đường thẳng vuông góc với BE cắt BC tại M và N. Tia ND cắt CA ở I. CM:
a, A là trung điểm của CI
b, CM=MN
Theo dõi (0) 1 Trả lời -


Tính các góc của tam giác ABC biết đường cao AH và trung tuyến AM chia góc BAC
bởi cuc trang
 09/04/2019
09/04/2019
Tính các góc của tam giác ABC. Biết rằng đường cao AH và trung tuyến AM chia góc \(\widehat{BAC}\) thành 3 góc bằng nhau
Theo dõi (0) 1 Trả lời -


Chứng minh AB+AC < BC+AH biết tam giác ABC vuông tại A có AH vuông góc BC
bởi Huong Duong
 10/04/2019
10/04/2019
Bài 1:
Cho tam giác ABC vuông tại A, AH vuông góc BC (H thuộc BC). Trên BC lấy điểm D sao cho BD=BA.C/m:
a, AD là phân giác của góc HAC
b, Vẽ DK vuông góc AC (K thuộc AC)
C/m : AK = AH
c, AB + AC < BC + AH
Theo dõi (0) 1 Trả lời -


Chứng minh AM là phân giác của góc EMF biết tam giác ABC cân có AB=AC, ME vuông góc AC
bởi thủy tiên
 10/04/2019
10/04/2019
∆ cân ABC (AB = AC). Từ trung điểm M của BC vẽ ME vuông góc AC; MF vuông góc AC. Chứng minh rằng
a) ∆BEM = ∆CFM
b) AE = AF
c) AM là phân giác của góc EMF
d) So sánh MC và ME
Help me :(
Theo dõi (0) 1 Trả lời -


Nêu giả thiết, kết luận và vẽ hình cho 2 trường hợp bằng nhau của tam giác vuông
bởi Lê Tấn Vũ
 25/02/2019
25/02/2019
Nêu giả thiết, kết luận và vẽ hình cho 2 trường hợp bằng nhau của tam giác vuông .
Giúp mình với . Mình tích nhé . THANK NHÌU
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A (AB > AC). BD là tia phân giác của góc B ( D thuộc AC ). Kẻ \(DH\perp BC\) ( H thuộc BC )
a, C/minh: BA = BH
b, Trên tia AC lấy E sao cho AE = AB. Đường thẳng vuông góc với AE tại E cắt DH tại K. Tính góc DBK
Theo dõi (0) 1 Trả lời -


Chứng minh BA_1=CA_2 biết tam giác ABC có AH là đường cao, AM là trung tuyến
bởi Nguyễn Vân
 10/04/2019
10/04/2019
Cho tam giác ABC có AH là đường cao, AM là trung tuyến. trên các tia đối của HA và MA lấy các điểm A1 va A2 sao cho HA1=HA va MA2=MA. Chứng minh BA1=CA2
Theo dõi (0) 1 Trả lời -


Chứng minh MH=MK biết góc nhọn xOy, Oz là tia phân giác của góc đó, MH vuông góc Ox
bởi Nguyễn Thủy Tiên
 10/04/2019
10/04/2019
Cho góc nhọn xOy, Oz là tia phân giác của góc đó. Qua điểm A thuộc tia Ox kẻ đường thẳng song song với Oy cắt Oz ở M. Qua M kẻ đường thẳng song song với Ox cắt Oy ở B.
a, CM: OA=OB, MA=MB
b, Từ M kẻ MH vuông góc với Ox, MK vuông góc với Oy. CM: MH=MK
Các bạn k cần vẽ hình giúp mk đâu, chỉ cần chỉ ra góc AMO=BMO ở câu a vs chỉ ra góc HMO=KMO ở câu b là đc
Các bạn cố gắng giúp mk nha

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh IH=IK biết tam giác ABC cân tại A có BH và CK vuông góc với AB, AC
bởi Nguyễn Trung Thành
 10/04/2019
10/04/2019
Cho tam giác ABC cân tại A, vẽ BH, CK, lần lượt vuông góc với AC,AB
a) Chứng minh BH=CK
b) Gọi I là giao điểm của BH và CK, chứng minh IH=IK
c ) từ b vẽ Bx vuông góc vưới AB, từ c vẽ Cy vuông góc với AC, Bx.Cy,cắt nhau ở d
chứng minh 3 điểm y,b,d thẳng hàng
mọi người ơi giúp em với ạ em đang cần gấp
Theo dõi (0) 1 Trả lời -


Chứng minh CE=CB biết tam giác ABC vuông tại A có AB=AC, K là trung điểm của BC
bởi minh vương
 10/04/2019
10/04/2019
cho tam giác ABC vuông tại A có AB=AC . Gọi K là trung điểm của cạnh BC
a) Chứng minh tam giác AKB = tam giác AKC vf AK vuông góc với BC
b) Từ C kẻ đường vuông góc với BC, nó cắt AB tại E. Chứng minh EC//AK
c) Chứng minh CE=CB
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A(A<90 độ ) . Kẻ BM vuôngg góc AC (M thuộc AC ) ,kẻ CN vuông góc AB ( N thuộc AB ) . Gọi K là giao điểm của BM và CN
a, AM =AN b AK là tia phân giác của góc BAC.
Theo dõi (0) 1 Trả lời -


Chứng minh BD là tia phân giác góc ABC biết tam giác ABC vuông tại A có AB=6cm, AC=8cm
bởi Mai Đào
 11/04/2019
11/04/2019
Cho tam giac ABC vuong tai A , AB=6cm Ac=8cm
a) tính BC
b) so sánh góc ABC và góc ACB
c) trên cạnh BC đặt điểm H sao cho BH=BA. Vẽ đường thẳng đi qua H vuông gọi với BC cắt AC tại D
chương minh tam giác ABD= tam giác HBD từ đó suy ra BD là tia phân giâc của góc ABC
d) hai đường thẳng BA và HĐ kéo dài cắt nhau tại E chung minh tam giác ADE cânTheo dõi (0) 1 Trả lời -


Chứng minh DK=KE biết tam giác ABC có AD vuông góc AB, AE bằng và vuông AC
bởi Đào Thị Nhàn
 11/04/2019
11/04/2019
Cho tam giác ABC. Vẽ đoạn thẳng AD bằng và vuông góc với AB (D và C nằm khác phía đối với AB). Vẽ đoạn thẳng AE bằng và vuông góc với AC (E và B nằm khác phía đối với AC). Vẽ AH vuông góc với BC. Đường thẳng HA cắt DE ở K. CMR: DK=KE
Theo dõi (0) 1 Trả lời -


Cho t/giác ABC nhọn,đg cao BD,CE cắt nhau ở H. Vẽ điểm K sao cho AB là đường trug trực của HK. CM góc KAB = góc KCB
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A,góc B =60 độ,đg cao AH
a, so sánh AB và AC, HB và HC
b,lấy D thuộc tia đối của tia AH sao cho HA=HD. CM: T/giác AHC= T/giác DHC
c, tính góc BDC
Theo dõi (0) 1 Trả lời -


Chứng minh MN đi qua trung điểm của DE biết AH vuông góc với BC, DM vuông góc với AH
bởi Nguyễn Thủy Tiên
 11/04/2019
11/04/2019
Cho tam giác ABC. Vẽ về phía ngoài tam giác ABC các tam giác vuông tại A là ABD, ACE có AB=AD, AC=AE. Kẻ AH vuông góc với BC, DM vuông góc với AH, EN vuông góc với AH. Chứng minh rằng:
a, DM=AH
b, MN đi qua trung điểm của DE
Theo dõi (0) 1 Trả lời -


Cho Δ ABC không vuông. Các đường trung trực của AB và AC cắt nhau tại O, cắt đường thẳng BC theo thứ tự ở M và N. Chứng minh rằng AO là tia phân giác của \(\widehat{MAN}\)
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A có góc A = 120 độ , AB = 6cm. Tính độ dài cạnh BC
Theo dõi (0) 1 Trả lời -


(Vẽ hình) Cho tam giác ABC cân tại A
a) Trên cạnh BC lần lượt lấy điểm D ,E sao cho BD=CE. (BD<BC phần 2) cm AD=AE
B) kẻ DF vuông góc AB tại F ; EG vuông góc AC tại G
Cm tam giác BDF = tam giác CEG
C) gọi H là giao điểm của FD và GE .cm tam giác DEH cân (mấy bạn vẽ hình và giải giúp mình nhé mình cảm ơn mấy bạn nhiều )
Theo dõi (0) 1 Trả lời -


Tính số đo các góc còn lại của tam giác DAE biết tam giác ABC có AB=AC, góc DEA=60 độ
bởi thúy ngọc
 11/04/2019
11/04/2019
Cho tam gíac ABC có AB=AC.D,E thuộc cạnh BC sao cho BD=DE=EC.Biết AD=AE
a)CM \(\widehat{EAB}\)=\(\widehat{DAC}\)
b)M là trung điểm của BC. Chứng minh AM là phân giác của \(\widehat{DEA}\)
c)Giả sử \(\widehat{DEA}\)=60 . tính các góc còn lại tam giác DAE
Theo dõi (0) 1 Trả lời -


Chứng minh AB=AI biết tam giác ABC vuông tại A có góc C=30 độ, tia phân giác góc A
bởi Thụy Mây
 11/04/2019
11/04/2019
Cho \(\Delta ABC\) vuong tai B co goc C=30 do. Tia phan giac cua goc A cat Bc tai D. Ke DI vuong goc voi AC (\(I\varepsilon\) AC)
a. Chung minh rang AB=AI
b. Goi M la giao diem cua ID va AB. Chung minh DM=MC
c. Chung minh \(\Delta MAC\) deu
d. Chung minh MD=2.DI
Theo dõi (0) 1 Trả lời -


Chứng minh AB=EF biết góc xOy=90 độ và OE=OB, OF=OA
bởi ngọc trang
 25/02/2019
25/02/2019
Cho góc xOy=90°.Trên tia Ox lấy điểm A,trên tia Oy lấy điểm B(OA<OB).Trên tia đối của tia Ox lấy điểm E,trên tia Oy lấy điểm F sao cho OE=OB,OF=OA
a)Chứng minh rằng AB=EF và AB⊥EF
b)Gọi M và N lần lượt là trung điểm của AB và EF.Chứng minh △OMN vuông cân
Theo dõi (0) 1 Trả lời






