Giải bài 93 tr 151 sách BT Toán lớp 7 Tập 1
Cho tam giác \(ABC\) cân tại \(A.\) Kẻ \(AD\) vuông góc với \(BC.\) Chứng minh rằng \(AD\) là tia phân giác của góc \(A.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Lời giải chi tiết
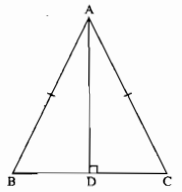
Xét hai tam giác vuông \(ADB\) và \(ADC\) có:
\(\widehat {A{\rm{D}}B} = \widehat {A{\rm{D}}C} = 90^\circ \)
\(AB = AC\) (vì \(\Delta ABC\) cân tại \(A\))
\(AD\) cạnh chung
\( \Rightarrow ∆ADB = ∆ADC\) (cạnh huyền - cạnh góc vuông).
\( \Rightarrow \widehat {BAD} = \widehat {CAD}\) (hai góc tương ứng).
Vậy \(AD\) là tia phân giác của góc \(A.\)
-- Mod Toán 7 HỌC247
-


Chứng minh tam giác BHM=tam giác CKM biết từ BC kẻ các đường vuông góc với AM
bởi Nguyễn Thị Lưu
 27/02/2019
27/02/2019
Cho △ABC ⊥ tại A có AB=3cm; AC=4cm. M là trung điểm của BC. Từ BC kẻ các đường vuông góc với đường thẳng AM, chúng cắt AM lần lượt tại H và K.
a. Tính BC
b. Cm: △BHM=△CKM
c. CM: 2(AH+MK)=BC
Theo dõi (0) 1 Trả lời -


Bài 1: Cho tam giác ABC vuông tại A, (AB < AC). D, E là các điểm thuộc AC, BC sao cho DE vuông góc với BC và DE=EB
a) Kẻ EH vuông góc với AB, EK vuông góc với AC. Chứng minh rằng tam giác EKD = tam giác DHB
b) Chứng minh AE là tia p/g \(\widehat{BAC}\)
Bài 2: Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm D, trên tia đối của CB lấy điểm E sao cho BD=CE. Kẻ BH vuông góc với AD (H thuộc AE). Chứng minh rằng:
a) BH = CK
b) Tam giác AHB = tam giác AKC
c) BC // HK
Bài 3: Cho tam giác ABC có AB = 24, AC = 32, BC = 40. Trên cạnh AC lấy điểm D sao cho AD = 7. Chứng minh rằng:
a) Tam giác ABC vuông
b) \(\widehat{AMB}\) = 2\(\widehat{C}\)Theo dõi (0) 1 Trả lời -


Tính các góc của tam giác OAB biết góc AMO=60 độ
bởi Lê Thánh Tông
 25/02/2019
25/02/2019
Cho góc nhọn xOy, Ot là tia phân giác lấy M thuộc Ot, từ M vẽ MA vuông góc với Ot, MB vuông góc Oy.Đường thẳng AM cắt Oy tại D, đường thẳng BM cắt Ox tại C. CHỨNG MINH: a) tình các góc của tam giác OAB, góc AMO=60 độ b) cho OA=12cm,OM=16cm . Tính MA và MB
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A. Gọi M là trung điểm của cạnh BC.
a ) Chứng minh : \(\Delta ABM=\Delta ACM\)
b ) Từ M vẽ \(MH\perp AB\) và \(MK\perp AC.\) Chứng minh BH = CK.
c ) Từ B vẽ \(BP\perp AC\) , BP cắt MH tại I. Chứng minh \(\Delta IBM\) cân.
VẼ HÌNH NHÉ @@@
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC, tia Ax đi qua trung điểm M của cạnh BC. Kẻ BE, CF vuông góc với Ax (E,F thuộc Ax). Chứng minh rằng:
a) tam giác BME = tam giác CMF b) BE=CF
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác BEC=tam giác CDB biết ABC cân ở A và các đường cao BD, CE
bởi hồng trang
 22/02/2019
22/02/2019
Cho \(\Delta ABC\)cân ở A. Kẻ các đường cao BD và CE. Trên tia đối của tia BA lấy điểm M, trên tia đối của tia CA lấy điểm N sao cho BM = CN. Chứng minh:
a) \(\Delta BEC=\Delta CDB\)
b) \(\Delta ECN=\Delta DBM\)
c) ED // MN
Theo dõi (0) 1 Trả lời -


Cho góc xOy nhọn; Ot là tia phân giác góc xOy. Trên Ot lấy điểm M bất kì. Kẻ MA vuông góc Ox tại A; MB vuông góc với Oy tại B. Trên tia đối của MO lấy điểm N/ MO=MN.
a, Chứng minh: OA=OB
b, Chứng minh: OM là đường trung trực của AB
c, Chứng minh: 2OM<OA+AN
d, Kéo dài tia AM cắt Oy tại C. So sánh OM và OC
e, Kéo dài tia BM cắt Ox tại D. Chứng minh MN vuông góc với CD
LÀm giúp mk với thứ 2 mk kiểm tra
Cảm ơn đã làm hộ mk
Theo dõi (0) 1 Trả lời -


Chứng minh AO là trung trực của BC biết BE vuông AC, CF vuông AB và BE=CF
bởi Đặng Ngọc Trâm
 25/02/2019
25/02/2019
Cho ΔABC,kẻ BE⊥AC và CF⊥AB,cho BE=CF.Gọi O là giao điểm của BE và CF
a)Chứng minh EF//BC
b)Chứng minh AO là trung trực của BCTheo dõi (0) 1 Trả lời -


cho tam giác abc có góc a bằng 90 độ, AB=AC. Qua A kẻ đường thẳng d sao cho B và C nằm cùng phía với d, kẻ BD vuông góc d, CE vuông góc d, D thuộc d, E thuộc d
CMR: BD=AE,AD=CETheo dõi (0) 1 Trả lời -


Cho tam giac ABC. Vẽ phía ngoài các tam giác ABC các tam giác vuông tại A là ABD, AEC có AB = AD, AC = AE. kẻ AH vuông với BC, DM vuông với AH, EN vuông với AH. CMR:
a) DM = EN
b) Gọi O là giao điểm của AN và DE. CMR O là trung điểm của DE.
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A. Trên cạnh BC lấy điểm M, kẻ \(ME\perp AB;MF\perp AC.\)Cmr : Tổng ME + MF không phụ thuộc vào điểm trên cạnh BC.
Theo dõi (0) 2 Trả lời -


cho hai tam giác vuông là ABC và DEF có A=D=90 độ,AC=DF. Hãy bổ sung thêm một điều kiện ( Về cạnh hay về góc) để tam giác ABC = tam giác DEF
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABH=tam giác ẠCK biết ABC cân tại A, BH vuông AC, CK vuông AB
bởi Cam Ngan
 22/02/2019
22/02/2019
Cho \(\Delta\)ABC cân tại A, \(\widehat{A}\) nhỏ hơn \(90^o\).VẼ BH\(\perp\)AC, CK\(\perp\)AB
a Chứng minh \(\Delta\)ABH = \(\Delta\)ACK
b chứng minh \(\Delta\) CBK = \(\Delta\)BCH
Theo dõi (0) 1 Trả lời -


Cho \(\Delta ABC\) có AB = AC, M là trung điểm của BC.
1. Chứng minh : \(\Delta AMB=\Delta AMC\)
2. Từ M kẻ ME \(\perp\)AB tại E, MF \(\perp\) AC tại F. Chứng minh : AE=AF
3.Chứng minh EF//BC
4.Từ B kẻ đường thẳng vuông góc với AB, từ C kẻ đường thẳng vuông góc với AC. Hai đường này cất nhau ở N. Chứng minh: A, M, N thẳng hàng
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A. Trên tia đối của tia BC và CB lấy theo thứ tự hai điểm D và E sao cho BD = CF.
a) Chứng minh tam giác ADE cân.
b) Gọi M là trung điểm của BC. Chứng minh AM là tia phân giác của góc DAE.
c) Từ B và C kẻ BH và CK theo thứ tự vuông góc với AD và AE. Chứng minh BH = CK.
d) Chứng minh 3 đường thẳng AM, BH, CK gặp nhau tại một điểm.
Theo dõi (0) 1 Trả lời -


cho tam giác ABC vuông cân tại A , biết AB=AC=4cm.
a) tinh độ dài cạnh bc
b) từ a kể AD vuông BC .chứng minh rằng :D là trung điểm của BC
c)từ d kẻ DE vuông AC .chứng minh rằng :tam giác AED là tam giác cân
d)tinh độ dai AD
Theo dõi (0) 1 Trả lời -


cho tam giác ABC cân tại A, kẻ đường cao AH (H thuộc BC)
a/ chứng minh : tam giác AHB= tam giác AHC
b/chứng minh : HB=HC và góc BAH=góc CAH
c/ cho BC=20cm, AB = 8cm.tính độ dài đoạn thẳng AH
d/ kẻ HD vuông góc AB (D thuộc AB), HE vuông góc AC ( E thuộc AC). chứng minh rằng tam giác HDE là tam giác cân
e/ chứng minh rằng DE//BC
Theo dõi (0) 1 Trả lời -


Bài1
Cho tam giác ABC có góc A=60° ,góc B=70°
a) So sánh các cạnh AB, AC, BC
b) Vẽ AD vuôg góc BC tại D.So sánh DB và DC
Bài 2
Cho tam giác ABC vuôg tại A, có AB=6cm,AC=8cm
a) Tính BC
b) Tia phân giác của góc ABC cắt AC tại D.Vẽ DE vuông góc vs BC tại E. CM tam giác ABD=tam giác EBD và tam giác BAE cân
c) Gọi F là giao điểm của 2 đường thẳng BA và ED so sánh hai đoạn thẳng DE và DF
M.n giúp mk vs ..c.mơn m.n.
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABH=tam giác ANH biết AH vuông góc với BC, H là trung điểm của BN
bởi Sam sung
 28/02/2019
28/02/2019
1. Tìm x , y :
a) \(\dfrac{2x}{5}\) - \(\dfrac{1}{3}\) = \(-1\dfrac{1}{2}\) : \(\dfrac{5}{4}\)
2. Tam giác ABC có góc A = 90độ , góc C = 20độ .
a) Tính số đo góc ABC ?
b) Kẻ AH vuông góc với BC . Trên tia BC lấy N sao cho H là trung điểm của BN . Chứng minh tam giác ABH = tam giác ANH .
c) Qua B kẻ đường thẳng song song với AN cắt AH tại K . Chứng minh H là trung điểm của AK .
HELP ME !!!!!!!!!!!!!!!!!!!
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC nhọn, hai đường cao BD,CE cắt nhau tại H.Cho AC=BH.Tính góc B
Theo dõi (0) 1 Trả lời -


Chứng minh AE + AF = 2AM biết BE và CF vuông góc với đường thẳng AM thứ tự tại E và F
bởi Phạm Hoàng Thị Trà Giang
 28/02/2019
28/02/2019
1) cho △ABC , góc B = góc C = 50độ , tính góc A ( Ko cần vẽ hình )
2) Cho△ABC ( AB < AC ) M là trung điểm của BC , kẻ BE và CF vuông góc với đường thẳng AM thứ tự tại E và F . CM
a) △BME = △CMF
b) AE + AF = 2AM
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A; \(M\in AB\) ; trên tia đối của CA lấy N sao cho \(BM=CN\). Gọi D, E thứ tự là hình chiếu của M, N trên đương thẳng BC. Gọi I là giao điểm của MN, BC
a/ Chứng minh I là trung điểm của MN
b/ Đường phân giác của góc BAC cắt đường trung trực của Mn tại Q. C.m QC vuông góc với AC
c/ Đường thẳng QA giao BC tại H. Chứng minh rằng \(QA^2=HA^2+HQ^2+\dfrac{BC^2}{2}\)
Theo dõi (0) 1 Trả lời -


Cho góc nhọn xOy. Gọi M là một điểm thuộc tia phân giác xOy kẻ MA vuông góc với Ox,MB vuông góc với Oy
a) CMR:MA=MB và tam giác OAB cân
b) Kéo dài BM cắt Ox tại D, AM cắt Oy tại E . CMR: MD=ME
c) CMR: OM vuông góc DE
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A, gócA<90 độ. Kẻ BD vuông gócAC(D thuộcAC), kẻ CE vuông gócAB(E thuộc AB). Gọi I là giao điểm của BD và CE. CMR:
a, AD=AE
b, AI là tia phân giác góc BAC
Theo dõi (0) 1 Trả lời -


Cho tam giác DMN cân tại D , kẻ MA ⊥ DN , NB ⊥ DM
a/ CM : tam giác AMD = tam giác BND
b/ CM : tam giác ANM = tam giác BMN
c/ Gọi I là giao điểm của AM và BN , CM : DI là tia phân giác của D
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABM= tam giác biết đường thẳng qua B//vs AC cắt DC tại N
bởi Nguyễn Thủy
 28/02/2019
28/02/2019
Cho tam giác ABC vuông tại A. gọi M là trung điểm của AC. trên tia đối MB lấy D / MD = MB. cmr:
a) AD=BC
b) CD vuông góc vs AC
C) vẽ đường thẳng qua B//vs AC cắt DC tại N. CMR: tam giác ABM= tam giác
*****************************
phan a,b) mk bít cách làm rồi
phần c) thì chưa
help me soon.
Theo dõi (0) 1 Trả lời -


Chứng minh DE = BD + CE biết tam giác ABC có góc A = 90 độ, BD và CE vuông góc với xy
bởi Nguyễn Hiền
 28/02/2019
28/02/2019
Cho tam giác ABC có góc A = 90 độ và AB = AC. Qua điểm A kẻ đường thẳng xy sao cho xy không cắt đoạn thẳng BC. Kẻ BD và CE vuông góc với xy
a) c/m tam giác ABD = tam giác CAE
b) c/m DE = BD + CE
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC có AB=AC. Tia phân giác của góc A cắt BC tại D
a) CMR : tam giác ADB= tam giác ADC
b) CMR: AD vuông góc BC
c) Kẻ DH vuông góc với AB (H thuộc AB), DK Vuông góc AC( K thuộc AC). Chứng minh DH=DK
Theo dõi (0) 1 Trả lời -


cho tam giác ABC cân có góc A=90 độ, hai điểm B và e thuộc BC sao cho BD=DE=EC, kẻ BH vuông AD, CK vuông AE ( H thuộc AD, K thuộc AE), BH giao với CK tại G. a) chứng minh rằng: BH=CK
b) M là trung điểm của BC và A,M,G thẳng hàng
c) AC> AD
d) góc DEA> góc DAB
Theo dõi (0) 1 Trả lời -


Bài 1: Cho tam giác nhọn, kẻ AH vuông góc với BC (H thuộc BC). Cho biết AC = 20 cm, AH = 12 cm, BH = 5 cm. Tính độ dai cạnh HC, BC
Bài 2: Cho tam giác ABC vuông tại A có AB = 9 cm, BC = 15 cm. Tính AC.
Bài 3: Cho hình vẽ bên, biết tam giác ABC vuông tại A, AH vuông góc BC (H thuộc BC). AB = 9 cm, AH = 7,2 cm, HC = 9,6 cm. Tính cạnh AC, BC.
Bài 4: Cho tam giác ABC cân tại A kẻ AH vuông góc BC (H thuộc BC)
a) CM: HB = HC
b) Kẻ HD vuông góc AB (D thuộc AB), HE vuông góc AC (E thuộc AC); Chứng minh tam giác HDE cân
c) Nếu cho góc BAC = 120 độ thì tam giác HDE trở thành tam giác gì? Vì sao?
d) Chứng minh: BC // DE
Bài 5: Cho tam giác ABC cân tại A. Kẻ BD vuông góc với AC, CE vuông góc với AB, AC = 16 cm. BD và CE cắt nhau ở I.
a) CM: Tam giác BDC = tam giác CEB
b) So sánh góc IBE và góc ICD
c) AI cắt BC tại H, chứng minh rằng AH vuông góc với BC tại H.
Bài 6: Cho tam giác ABC cân tại A, lấy M là trung điểm của BC. Vẽ hình
a) Cho AB = 4 cm. Tính cạnh AC
b) Nếu cho góc B = 60 độ thì tam giác ABC là tam giác gì? Giải thích ?
c) CM: tam giác AMB = tam giác AMC
d) CM: AM vuông góc BC
e) kẻ MH vuông góc AB ( H thuộc AB ), MK vuông góc AC ( K thuộc AC ). CM MH = MK.
Bài 7: Cho góc xOy = 120 độ, A thuộc tia phân giác của góc đó. Kẻ AB vuông góc Ox, AC vuông góc Oy. Tam giác ABC là tam giác gì? Vì sao ?
~ Giúp mk nha mai mình nôp r ❤️ ~
~ M.n vẽ hình giải đầy đủ giùm mk nha, trừ bài 7 và 3 m.n khỏi vẽ hình nha ~
~ Thanks nhìu ❤️ ~
Theo dõi (0) 1 Trả lời -


Chứng minh góc C=góc E biết tam giác ABC và DEF vuông tại A, D có B=F
bởi Nguyễn Thủy Tiên
 28/02/2019
28/02/2019
Chứng Minh góc C = góc E
Theo dõi (0) 1 Trả lời -


Chứng minh BH là tia phân giác góc ABC biết tam giác ABC có AB=3cm, BC=15 cm
bởi Nguyễn Thị Thu Huệ
 25/02/2019
25/02/2019
Bài 1 Cho tam giác ABC vuông tại A có BC = 2A CD phân giác của góc c cắt AB tại D Gọi M là trung điểm của bc A chứng minh BC = b b và d m vuông góc với BC b tính các góc của tam giác ABC
Bài 4 Cho tam giác ABC có AB bằng 3 cm BC 15 cm AC bằng 4 cm a tam giác ABC là tam giác gì Vì sao B trên cạnh BC lấy điểm D sao cho b a = BC từ D kẻ d x vuông góc với BC và cắt AC tại H Chứng minh rằng bài hát là tia phân giác của góc ABC C và M là trung điểm của BC chứng minh tam giác AMC cân
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác IHC= tam giác IKB biết BH vuông góc với AC, CK vuông AB
bởi Nguyễn Phương Khanh
 22/02/2019
22/02/2019
Bài 1: Cho tam giác ABC từ B kẻ BH vuông góc với AC, từ C kẻ CK vuông góc với AB.Gọi I là giao điểm của BH và CK biết IK=CK
a,Chứng minh: tam giác IHC= tam giác IKB
b, Chứng minh:tam giác HAB= tam giác KAC
c, Chứng minh: AI là phân giác của góc BAC
d,Gọi D là giao điểm của AI và BC.Chứng minh: A vuông góc với BC
Giúp mk vs mk đang cần gấp!!!
Theo dõi (0) 1 Trả lời -


Chứng minh HE vuông góc với AB biết AH vuông góc với BC, trên BC lấy D sao cho HB = HD
bởi Xuan Xuan
 28/02/2019
28/02/2019
Cho tam giác ABC : Â = 90 độ, C = 30 độ, AH vuông góc với BC, trên BC lấy D sao cho HB = HD, kẻ CE vuông góc với AD (E thuộc AD) .Chứng minh :
a/ tam giác ABD đều, D là trung điểm of BC
b/ HE vuông góc với AB
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABD=tam giác IBD biết ABC vuông tại A, BD phân giác góc B
bởi Nguyễn Hiền
 22/02/2019
22/02/2019
Cho tam giác ABC vuông tại A , BD là phân giác của B . Vẽ DI vuông góc với BC ( I thuộc BC ) . Gọi K là giao điểm của DI và AB
a, CM : TAM GIÁC ABD = TAM GIÁC IBD
b, CM : BD vuông góc AI
c , CM : DK = DC
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông ở C, có góc A=600. Tia phân giác của góc A cắt BC ở E. Kẻ EK vuông góc với AB (K thuộc AB). Kẻ BD vuông góc với AE (D thuộc AE). Chứng minh:
a)AC=AK
b)BD=CK
MỌI NGƯỜI CỐ GẮNG GIẢI SỚM BÀI TOÁN NÀY GIÚP EM NHA! EM CẢM ƠM:D :)
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A (góc A < 90 độ). Vẽ AH vuông góc với BC tại H.
a. Chứng minh tam giác AHC = tam giác AHB
b. Kẻ HM vuông góc với AC tại M. Trên tia đối của tia HM lấy điểm N sao cho HN=HM. Chứng minh: BN // AC
c. Kẻ HQ vuông góc với AB tại Q. Chứng minh BC là đường trung trực của NQ
* Mk chỉ cần câu c thôi
Theo dõi (0) 1 Trả lời -


Cho góc xoy < 90°. Trên tia phân giác ot của góc xoy lấy điểm M. Kẻ MH vuông góc với ox, MK vuông góc với oy.
A... C/m MH=MK
B... Tam giác OMK là tam giác gì? Vì sao?
C... C/m ot vuông góc với HK.
Theo dõi (0) 1 Trả lời -


Chứng minh AB=AC biết tam giác ABC có B=C
bởi Ngoc Nga
 22/02/2019
22/02/2019
Cho \(\Delta\)ABC có \(\widehat{B}=\widehat{C}\)
C/M AB=AC
Theo dõi (0) 1 Trả lời -


Chứng minh BC=BE biết tam giác ABC vuông tại A, tia phân giác góc B cắt AC tại D
bởi Nguyễn Hoài Thương
 28/02/2019
28/02/2019
1. Cho tam giác ABC vuông tại A . Tia phân giác của góc B cắt cạnh AC tại D. Kẻ DH ⊥ BC tại H.
a) C/M : △ABC =△HBD
b) Hai đường thẳng DH và AB cắt nhau tại E. C/m BC=BE
c) C/m :AD < DC
( Giúp mik cái nha, mình sắp nộp rồi)
Theo dõi (0) 1 Trả lời -


Cho góc nhọn xOy. Gọi I là một điểm thuộc tia phân giác của góc xOy. Kẻ IA vuông góc với Ox (điểm a thuộc tia Ox) và IB vuông góc với Oy (điểm B thuộc tia Oy)
a) chứng minh IA=IB
b)cho biết OI=10cm, Ai=6cm. Tính OA
c) gọi K là giao điểm của BI và Ox và M là giao điểm của AI với Oy. so sánh AK và BM
d) gọi c là giao điểm của OI và MK. Chứng minh OC vuông góc với MK
Theo dõi (0) 1 Trả lời -


Cho ∆ABC có AB=3cm, BC=4cm , AC=5cm
a/chứng minh ∆ABC vuông tại B
b/ vẽ phân giác AM (Mt thuộc BC).từ M vẽ MN vuông với AC (N thuộc AC ).chứng minh ∆ ABM = ∆ ANM
c/ đường thẳng NM cắt đường thẳng AB tại K.chứng minh MK > MN.
d/chứng minh AM vuông góc với KC
Theo dõi (0) 1 Trả lời -


Cho tam giác NMP cân tai N.trên tia đối của tia MP lấy điểm A , trên tia đối của tia PM lấy điểm B sao cho MA=BM
a, chứng minh rằng tam giác NAB là tam giác cân.
b, kẻ MH ,NA (H\(\in\)NA)kẻ PH,NB(k\(\in\)NB).chứng minh MH=Pk
Theo dõi (0) 1 Trả lời -


Cho △ABC vuông tại A có AB = AC. Gọi K là trung điểm của BC
a) CMR △AKB = △AKC; AK ⊥ BC
b) Từ C vẽ đường thẳng vuông góc với BC cắt AB tại E. CMR EC song song AK
c) Tính \(\widehat{BEC}\)Theo dõi (0) 1 Trả lời -


Chứng minh HA=HE biết tam giác ABC vuông tại A có AB < AC và AH vuông BC
bởi Phan Thiện Hải
 25/02/2019
25/02/2019
Cho tam giác ABC vuông tại A có AB < AC.Vẽ \(AH\perp BC\) \(\left(H\in BC\right)\), D là điểm trên cạnh AC sao cho AD = AB. Vẽ \(DE\perp BC\left(E\in BC\right)\). Chứng minh HA = HE
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác AED=AFD và AD là trung trực của EF biết D là trung điểm BC
bởi Nguyen Ngoc
 28/02/2019
28/02/2019
Cho tam giác cân ABC (AB=AC). Gọi D là trung điểm của BC, từ D hạ DE, DF vuông góc với AB, AC theo thứ tự (E thuộc AB, F thuộc AC).
a) Cm: tam giác AED=AFD và AD là trung trực của EF.
b) Trên tia đối của tia DE lấy điểm K sao cho DK=DE. Cm: Tam giác EKC vuông.
c) So sánh BF và EK.
Theo dõi (0) 1 Trả lời -


1. Hình :
Tam giác.ABC vuông tại A có AB = 3cm , AC = 4cm .
a) Tính BC ?
b) Vẽ đường phân giác BD của tam giác ABC ( D thuộc AC ) . Kẻ DE vuông góc với BC tại E . Chứng minh tam giác ABD = tam giác EBD .
c) Lấy K thuộc tia đối của AB . Chứng minh AK = EC .
HELP ME !!!!!!!!!!!!!!!!!!
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân A
a) Biết góc B =60 độ
b) Kẻ AH vuông góc BC (H thuộc BC).CM: H là trung điểm BC
c) Biết AH=4cm, BC= 6cm.Tính AB
d) Nếu góc HAC = 30 độ thì tam giác ABC là tam giác gì ? Vì sao
Theo dõi (0) 1 Trả lời -


Cho góc nhọn xOy. Gọi Y là 1 điểm thuộc tia phân giác xOy. Kẻ IA vuông góc Ox, BI vuông góc với Oy.
a) CM IA = IB
b) Cho biết OI = 10cm, AI = 6cm. Tính OA.
c) Gọi K là giao điêm của BI và Oy, M là giao điểm của AI và Oy. SO sánh Ak và BM
d) Gọi C là giao điểm của OI và MK. CM OC vuông góc MK
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A và AB = AC. Qua đỉnh A kẻ đường thẳng xy sao cho xy không cắt đoạn thẳng BC. Kẻ BD và CE vuông góc với xy ( D ∈ xy, E ∈ xy ).Chứng minh
a) Góc DAB = Góc ACE
b) ∆ABD = ∆CAE
c) DE = BD + CE
Theo dõi (0) 1 Trả lời -


Tam giác HEF là tam giác gì biết HE vuông AC, HF vuông AB?
bởi Bo Bo
 28/02/2019
28/02/2019
cho tam giác ABC cân tại A.Kẻ AH vuông góc BC(A thuộc BC)
a)chứng minh BH=HC
b)kẻ HE vuông AC (E thuộc AC),HF vuông AB (F thuộc AB).hỏi tam giác HEF là tam giác gì?vì sao?
giúp mik vs mn ơi
cảm ơn nhiều nhé
Theo dõi (0) 1 Trả lời -


Chứng minh góc BAD=gó ADH biết tam giác ABC vuông tại A, DH vuông AC
bởi Nguyễn Lê Thảo Trang
 25/02/2019
25/02/2019
Cho tam giác ABC vuống tại A, điểm D thuộc cạnh BC. Kẻ DH vuông góc với AC( H thuộc Ac). Trên tia đối cảu tia HD lấy điểm E sao cho HE = HD. Chứng minh
a) Góc BAD = góc ADH
b) AD = AE
c) Góc BAD = góc AEH
d) Cho biết góc B = 50 độ và AD là phân giác của góc BAC tính góc ADC
Theo dõi (0) 1 Trả lời -


Chứng minh BK vuông góc AN biết KN vuông góc BC, M là giao điểm của AB và NK
bởi Nguyễn Thị Thu Huệ
 28/02/2019
28/02/2019
Cho tam giác ABC có góc A = 90 và đường phân giác BK ( K€ AC. Kẻ KN vuông góc BC ( N € BC ). Gọi M là giao điểm của AB và NK Chứng minh a, Tam giác ABK = Tam giác NBK. b, BK vuông góc AN. c, BK là đường trung trực của AN. d, BK vuông góc CM
Theo dõi (0) 1 Trả lời -


Chứng minh BN=AM biết OM=ON, AM cắt BN tại I
bởi sap sua
 22/02/2019
22/02/2019
cho góc xOy nhọn ; M thuộc Ox ,N thuộc Oy sao cho OM=ON.Từ M kẻ đường thẳng vuông góc với Ox cắt Oy tại A.Từ N ke đường thẳng vuông góc với Oy cắt Ox tại B;AM cắt BN tại I
a.cm BN=AM
b.Tia OI là pg của xOy
c.Tam giác IBA cân
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A . Trên tia đối của BC lấy điểm M, trên tia đối của CB lấy điểm N sao cho BM = CN.
a) Chứng minh: △ABM = △ ACN
b) Kẻ BH ⊥ AM ; CK ⊥ AN ( H thuộc AM; K thuộc AN ) . Chứng minh : AH = AK
c) Gọi O là giao điểm của HB và KC . Tam giác OBC là tam giác gì ? Vì sao
Theo dõi (0) 1 Trả lời -


Cho △ABC có 3 góc đều nhọn,kẻ đường cao AH.Kẻ Hx⊥AB tại M,Hy⊥AC tại N.Trên tia Hx lấy D sao cho MD=MH,trên Hy lấy E sao cho NH=NE
a)Tính góc DAE biết góc BAC=60°
b)DE cắt AB,AC lần lượt tại I và K.Chứng minh HA là tia phần giác của góc IHK
c)Chứng minh HB là tia phần giác ngoài của △HIK tại đỉnh H
Theo dõi (0) 1 Trả lời -


cho tam giác ABC vuông tại A, đường phân giác BE (E thuộc AC).Kẻ EH vuông góc với BC (H thuộc BC) . Gọi K là giao điêm của AB và HE
a) Tính độ dài AC , biết AB=6cm , BC=10 cm
b) cm AB = HB ; AE< EC
c) cm BE vuông góc CK ; AH // KC
d) nếu ABC = 60o thì Δ BAH là tam giác gì , vì sao ?Theo dõi (0) 1 Trả lời -


Cho ▲ABC cân tại A có AB=AC=5cm ;BC=8cm.Tia phân giác của góc A cắt BC ở I
Chứng minh :a,▲AIB=▲AIC
b,Tính AI
c, Từ I kẻ IM⊥AB , IN⊥AC.
Chứng minh ▲IMA=▲INA
d,Chứng minh IC>IM
VẼ HÌNH CHO MK LUÔN VS
Theo dõi (0) 1 Trả lời -


Nếu một cạnh góc vuông và một góc nhọn của tam giác vuông này...đúng hay sai?
bởi Anh Nguyễn
 24/10/2018
24/10/2018
Nếu một cạnh góc vuông và một góc nhọn của tam giác vuông này bằng một cạnh góc vuông và mot góc nhọn của tam giác vuông kia thì hai tam giac vuông đó bằng nhau đúng hay sai
Theo dõi (0) 2 Trả lời
Bài tập SGK khác
Bài tập 65 trang 137 SGK Toán 7 Tập 1
Bài tập 66 trang 137 SGK Toán 7 Tập 1
Bài tập 94 trang 151 SBT Toán 7 Tập 1
Bài tập 95 trang 151 SBT Toán 7 Tập 1
Bài tập 96 trang 151 SBT Toán 7 Tập 1
Bài tập 97 trang 151 SBT Toán 7 Tập 1
Bài tập 98 trang 151 SBT Toán 7 Tập 1
Bài tập 99 trang 151 SBT Toán 7 Tập 1






