Bài tập 4 trang 7 SGK Toán 9 Tập 1

Tính giá trị các biểu thức sau

1.\(\dfrac{1}{\sqrt{1}-\sqrt{2}}-\dfrac{1}{\sqrt{2}-\sqrt{3}}+\dfrac{1}{\sqrt{3}-\sqrt{4}}-\dfrac{1}{\sqrt{4}-\sqrt{5}}+\dfrac{1}{\sqrt{5}-\sqrt{6}}-\dfrac{1}{\sqrt{6}-\sqrt{7}}+\dfrac{1}{\sqrt{7}-\sqrt{8}}-\dfrac{1}{\sqrt{8}-\sqrt{9}}\)

2.\(\dfrac{1}{2\sqrt{1}+1\sqrt{2}}+\dfrac{1}{3\sqrt{2}+2\sqrt{3}}+\dfrac{1}{4\sqrt{3}+3\sqrt{4}}+\dfrac{1}{5\sqrt{4}+4\sqrt{5}}+\dfrac{1}{6\sqrt{5}+5\sqrt{6}}+\dfrac{1}{7\sqrt{6}+6\sqrt{7}}\)

giúp mk vs ạ

C/m A, B ∈ Z, với:

A= \(\sqrt{6-2\sqrt{5}}-\sqrt{6+2\sqrt{5}}\)

B= \(\dfrac{\sqrt{3-2\sqrt{2}}}{\sqrt{17-12\sqrt{2}}}-\dfrac{\sqrt{3+2\sqrt{2}}}{\sqrt{17+12\sqrt{2}}}\)

Help me

Tính:

a.\(\left(\sqrt{3}+\sqrt{5}\right)\sqrt{7-2\sqrt{10}}\)

b.\(\left(2+\sqrt{5}\right)\sqrt{9-4\sqrt{5}}\)

Cho 3 số dương a,b,c có tổng bằng 1. Tính giá trị nhỏ nhất của biểu thức P= 1/ab+bc+ac

Giải pt:

\(\sqrt{18x+9}-\sqrt{8x+4}+\dfrac{1}{3}\sqrt{2x+1}=4\)

Tính thu gọn :

a , \(\sqrt{17-12\sqrt{2}}-\sqrt{17+12\sqrt{2}}\)

b , \(\sqrt{27+12\sqrt{5}}-\sqrt{27-12\sqrt{5}}\)

c , \(\sqrt{15-6\sqrt{6}}+\sqrt{15+\sqrt{6\sqrt{6}}}\)

d , \(\sqrt{4+\sqrt{15}}+\sqrt{4-\sqrt{15}}-2\sqrt{3-\sqrt{5}}\)

e , \(\sqrt{17-3\sqrt{32}}+\sqrt{17+3\sqrt{32}}\)

f , \(\sqrt{5+\sqrt{3-\sqrt{29-12\sqrt{5}}}}\)

Tính giá trị:

A=\(\left(x^3-4x+1\right)^{2017}\) với x=\(\dfrac{\sqrt[3]{10+6\sqrt{3}}\left(\sqrt{3}-1\right)}{\sqrt{6+2\sqrt{5}}-\sqrt{5}}\)

A=\(\dfrac{2\sqrt{x}-9}{x-5\sqrt{x}+6}-\dfrac{3}{x\sqrt{x}+1}+\dfrac{2}{x-\sqrt{x}+1}\)

B=\(\dfrac{1}{\sqrt{x}+1}-\dfrac{3}{x\sqrt{x}+1}+\dfrac{2}{x-\sqrt{x}+1}\)

Tìm GTNN :

a , \(A=x^2+2\)

b , \(B=2x^2-4x\)

c , \(C=\sqrt{x^2+4x+5}\)

d , \(D=1+\sqrt{x+2}\)

e, \(E=\sqrt{x^2+1}\)

Giá trị nhỏ nhất của \(x^2-2x+y^2-4y+7\) là

Giair: \(\sqrt{x^2-2x+1}\) + \(\sqrt{x^2-4x+4}\) = 3

b) \(\sqrt{x^2-9}\) + \(\sqrt{x^2-6x+9}=0\)

Giari: \(\sqrt{x^2+2x+1}\) = \(\sqrt{x+1}\)

Giải pt sau:

\(\dfrac{\sqrt{x}-2}{\sqrt{x}-5}=\dfrac{\sqrt{x}-4}{\sqrt{x}-6}\)

Tính giá trị biểu thức :

\(P=\sqrt{1+\dfrac{1}{2^2}+\dfrac{1}{3^3}}+\sqrt{1+\dfrac{1}{3^2}+\dfrac{1}{4^2}}+...+\sqrt{1+\dfrac{1}{99^2}+\dfrac{1}{100^2}}\)

giải phương trình

\(2\sqrt{3x-2}-2=11x+\sqrt{5x+6}-3\sqrt{\left(3x-2\right)\left(5x+6\right)}\)

Cho x , y , z \(\ne0\) thỏa mãn x + y + z = 0 .

CMR : \(\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}}=\left|\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right|\)

\(\sqrt[3]{7+5\sqrt{2}}+\sqrt[3]{7-5\sqrt{2}}\)

Chứng tỏ rằng x là nghiệm của phương trình : \(x^3+3x-14=0\)

giải phương trình sau:

\(\dfrac{\sqrt{x}+3}{\sqrt{x}-3}=2\)

Tìm x:

√x²-6x+9=√4+2√3

Help me, đang cần gấp

Giải pt

\(5\sqrt[3]{x+1}+1\sqrt{x+2}+5\sqrt[3]{x+3}=0\)

Tìm GTNN

P=\(\sqrt{x+1}\)-\(\sqrt{x-8}\)

Sbd help ~~ À mà ko cần giải phần rút gọn đâu a~ Chỉ cần hộ mik cách làm cái tìm GTNN là đc rùi ạ <3

P= \(\left\{\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}}{\sqrt{x}-3}-\dfrac{3x+3}{x-9}\right\}:\left\{\dfrac{2\sqrt{x}-2}{\sqrt{x}-3}-1\right\}\)

Tìm x để P có GT nhỏ nhất .

\(\)Mn giúp mình vs.. mình đang cần gấp ạ, cảm ơn mn nhiều lắm.. hjx

\(\sqrt{46-6\sqrt{ }5}-\sqrt{29-12\sqrt{ }5}\)

\(\sqrt{7-3\sqrt{ }5}\)

\(\left(3-\sqrt{ }2\right)\sqrt{11+6\sqrt{ }2}\)

\(\sqrt{4+\sqrt{ }15}\)

\(\left(\sqrt{ }5+\sqrt{ }7\right)\sqrt{12-2\sqrt{ }35}\)

\(\sqrt{17-12\sqrt[]{}2}\)

\(\sqrt{14-6\sqrt{ }5}\)

\(\sqrt{27-12\sqrt{ }5}\)

Bài 1: Chứng minh rằng (x, y, z > 0)

Bài 2: Cho a + b + c > 0; abc > 0; ab + bc + ca > 0. Chứng minh rằng a > 0; b > 0; c > 0.
Bài 3: Chứng minh rằng (a, b, c > 0)

Bài 4: Chứng minh rằng (a + b) (b + c) (c + a) 8abc (a, b, c 0)
Bài 5: Chứng minh rằng (a, b, c, d 0)
Bài 6: Cho x, y, z > 0 thỏa mãn .
Chứng minh .
Bài 7: Cho a, b, c là độ dài 3 cạnh của 1 tam giác. Chứng minh rằng (a+b-c) (b+c-a) (c+a-b) ab.
Bài 8: Cho x, y, z > 0; x+y+z = 1. Chứng minh rằng .
Bài 9: Cho 2 số có tổng không đổi. Chứng minh rằng tích của chúng lớn nhất khi và chỉ khi 2 số đó bằng nhau.
Bài 10: Cho a, b, c > 0. Chứng minh rằng .

Chứng mỉnh rằng

\(\sqrt{5\sqrt{5\sqrt{5...\sqrt{5\sqrt{5}}}}}+\sqrt{6+\sqrt{6+\sqrt{6+...+\sqrt{6+\sqrt{6}}}}}< 8\)

Rút gọn biểu thức : P = 3\(\sqrt{4x^6}\) - 3x³ với x < 0

choa,b,c là các số thực dương CMR:

\(\dfrac{a^2}{bc}+\dfrac{b^2}{ca}+\dfrac{c^2}{ab}\ge\dfrac{3\left(a^2+b^2+c^2\right)}{a+b+c}\)

tìm điều kiện xác định của các biểu thức sau: a,\(\sqrt{x+3}+\sqrt{3-x}\)

\(\dfrac{1}{\sqrt{x^2-1}}\)+

So sánh

a.5+ căn 47 và căn 40 + căn 23

b.căn 24 + căn 80 và 14

c.căn 62 + căn 35 và 15

giải phương trình

a)\(\dfrac{\sqrt{x}-2}{\sqrt{x}-4}=\dfrac{\sqrt{x}-6}{\sqrt{x}-7}\)

b)\(2+\sqrt[3]{x+5}=0\)

c)0,5\(\sqrt{\dfrac{2}{x}}-\sqrt{\dfrac{8}{25x}}+\sqrt{\dfrac{1}{4x}}=\dfrac{1}{5}\)

M=\(\left(1-\dfrac{4\sqrt{x}}{x-1}+\dfrac{1}{\sqrt{x}+1}\right)\)/\(\left(\dfrac{x-2\sqrt{x}}{x-1}\right)\)

Rút gọn M

giúp mik với các bạn ơi

\(\dfrac{x-3}{\sqrt{x-1}-\sqrt{2}}\)

Tìm giá trị của x thuộc Z để các biểu thức sau có giá trị nguyên:

\(\dfrac{3}{\sqrt{x}+2}\)

tìm giá trị lớn nhất của biểu thức: C = 7 - \(\sqrt{x^2-6x+9}\)

\(\sqrt{x+\sqrt{6x-9}}+\sqrt{x-\sqrt{6x-9}}=\sqrt{6}\)

tim x , biet: \(\sqrt{x^2}\)|x+2|=x

Cho a , b >0 thỏa mãn \(\dfrac{1}{a^2}+\dfrac{1}{b^2}=2\)

Chứng minh : a +b ≥ 2

\(\sqrt{4x+1}\) -\(\sqrt{3x+4}\) = 1

\(\sqrt{\sqrt{9}+1}+\sqrt{\sqrt{16}+5}\)

P=\(\dfrac{a}{\sqrt{a}-1}-\dfrac{2a-\sqrt{a}}{a-\sqrt{a}}\)

a) ĐKXĐ và Rút gọn

b) tính giá trị của P khi a=\(3-\sqrt{8}\)

c) tìm a để :P>0

1. rút gọn

A=\(\sqrt{9x^2-2x}\)

2.so sánh

\(\sqrt{3}\) và 5- \(\sqrt{8}\)

3. tìm GTNN

M=\(\sqrt{\dfrac{x^2}{4}-\dfrac{x}{6}+1}\)

Cho a,b,c thuộc Q, abc khác 0, a+b+c=0

CMR: P=\(\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}}\) là số hữu tỷ

Tính M=\(\sqrt{15x^2-8x\sqrt{15}+16}\) với x=\(\sqrt{\dfrac{3}{5}}+\sqrt{\dfrac{5}{3}}\)

a - \(4\sqrt{a}-5\)

\(1:\) Chứng minh rằng \(:\) \(\left|A+B\right|\) \(\le\) \(\left|A\right|+\left|B\right|\) \(.\) Dấu \("="\) xảy ra khi nào?

GIÚP MK NHA CÁC BN THANKS YOU CÁC BN NHÌU !!!

\(\dfrac{1}{2+\sqrt{3}}-\dfrac{1}{2-\sqrt{3}}\)

Giúp mk với, tối học r

Cho tam giác ABC vuông tại A,đường cao AH. Biết AC=20cm,AH=12cm.

a,Tính diện tích tam giác ABC

b, Kẻ HD vuông góc AB, HE vuông góc AC. CMR: HB:HC=AC^2/AD^2

c, CMR: BD/CE=AC^3/AB^3

tìm GTNN

\(\sqrt{\dfrac{x^2}{4}-\dfrac{x}{6}+1}\)

\(\dfrac{1}{3+\sqrt{5}}+\dfrac{1}{3-\sqrt{5}}\)

\(\dfrac{1}{2+\sqrt{2}}+\dfrac{1}{2-\sqrt{2}}\)

\(\left(\sqrt{24}-2\sqrt{12}+\sqrt{6}\right)\sqrt{6}+6\sqrt{8}\)

\(\left(\sqrt{28}-2\sqrt{14}+\sqrt{7}\right)\sqrt{7}+7\sqrt{8}\)

\(2\sqrt{27}-3\sqrt{12}\sqrt{\left(2-\sqrt{3}\right)^2}\)

Tìm giá trị lớn nhất của A

A = 2x + \(\sqrt{4-2x^2}\) với -\(\sqrt{2}\) ≤ x ≤ \(\sqrt{2}\)

\(\sqrt{\left(-3\right)^2}-2\left(-\sqrt{2}\right)^2+\sqrt{4}\)

\(\sqrt{\left(x^2-4x+4\right)}=2x-3\)

\(\sqrt{\left(2x+3\right)^2}=3\)

Cho số thực \(a\ge6\)Tìm giá trị nhở nhất A=\(a^2+\frac{18}{a} \)

Giải pt sau: \(\dfrac{\sqrt{x+5}}{\sqrt{x-4}}\) =\(\dfrac{\sqrt{x-2}}{\sqrt{x+3}}\)

\(\sqrt{\left(x-5\right)^2}=8\)

\(\dfrac{1-x\sqrt{x}}{1-\sqrt{x}}\)(x\(\ge\)0; x\(\ne\)1)

tìm GTNN

y=\(\sqrt{5+x^2-2x}\)

\(\dfrac{1}{\sqrt{2}+1}+\dfrac{1}{\sqrt{3}+\sqrt{2}}+\dfrac{1}{\sqrt{4}+\sqrt{3}}\)

tính giá trị biểu thức: c, \(\sqrt{2+\sqrt{3}}+\sqrt{14-5\sqrt{3}}+\sqrt{2}\)

tính giá trị biểu thức : b, \(\sqrt{4+\sqrt{7}}-\sqrt{4-\sqrt{7}}\)

tính giá trị biểu thức : a, \(\sqrt{21+6\sqrt{6}}+\sqrt{21-6\sqrt{6}}\)

cho a,b,c > 0 sao cho a+b+c = 3abc. T ìm GTNN của P = \(\dfrac{1}{a^5}+\dfrac{1}{b^5}+\dfrac{1}{c^5}\)

( dùng BĐT cosi)

Mn giúp e vs ạ.. e đg cần gấp, cảm ơn mn nhiều lắm ạ

Q=\(\dfrac{x-3\sqrt{ }x-4}{x-\sqrt{ }x-12}\)

\(P=\dfrac{x\sqrt{y}-y\sqrt{x}}{\sqrt{ }x-\sqrt{ }y}\)

Giải phương trình \(\sqrt{x-\sqrt{6x-9}}+\sqrt{x+\sqrt{6x-9}}=\sqrt{6}\)

tí nữa mình phải đi học rồi mong các bạn giúp đỡ

Chứng minh;

a, \(\left(\dfrac{1+a+\sqrt{a}}{\sqrt{a}+1}\right)\cdot\left(1-\dfrac{a-\sqrt{a}}{\sqrt{a}-1}\right)=1\)

Cho các số thực dương x² + y² + z² = 3

Chứng minh rằng : \(\frac{x}{\sqrt[3]{yz}}+\frac{y}{\sqrt[3]{xz}}+\frac{z}{\sqrt[3]{xy}}\ge xy+yz+xz\)

(√28-2√14+√7)√7+7√8

Tìm \(x;y\in N\)tmãn : \(\sqrt{x}+\sqrt{y}=\sqrt{2012}\)

2, Rút gọn bt

\(P=\dfrac{x}{x-\sqrt{x}}+\dfrac{2}{x+2\sqrt{x}}+\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+2\sqrt{x}\right)}\)

b, gpt : \(x^2-2x-x\sqrt{x}-2\sqrt{x}+4=0\)

3, cho x>1 ; y>0 , cm

\(\dfrac{1}{\left(x+1\right)^3}+\left(\dfrac{x-1}{y}\right)^3+\dfrac{1}{y^3}\ge3\left(\dfrac{3-2x}{x-1}+\dfrac{x}{y}\right)\)

Unruly Kid

Giải pt sau :

\(x^2-3x+1+\dfrac{\sqrt{3}}{3}.\sqrt{x^4+x^2+1}=0\)

Rút gọn B = \(\dfrac{2.\left(x+4\right)}{x-3\sqrt{x}-4}+\dfrac{\sqrt{x}}{\sqrt{x}+1}-\dfrac{8}{\sqrt{x}-4}\) (Đk x\(\ge\) 0, x\(\ne\)16)

Chứng minh rằng:

\(\sqrt{\dfrac{6\sqrt{3}-8}{2\sqrt{3}+1}}-\sqrt{3}=-1\)

Chứng minh: (\(\left(\sqrt{12}-6\sqrt{3}+\sqrt{24}\right)\sqrt{6}-\left(5\sqrt{\dfrac{1}{12}}+12\right)=-14,5\sqrt{2}\)

\(\left(2-\sqrt{3}\right)\left(\sqrt{2}+\sqrt{6}\right)\sqrt{2+\sqrt{3}}\)

\(\sqrt{4-\sqrt{7}}-\sqrt{4+\sqrt{7}}\)

cau a cho x,y,z\(\ne\)0 thoa man x+y+z=0. CM: \(\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}}=|\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}|\) cau b tinh G=\(\sqrt{1+\dfrac{1}{2^2}+\dfrac{1}{3^2}}+\sqrt{1+\dfrac{1}{3^2}+\dfrac{1}{4^2}}+\sqrt{1+\dfrac{1}{4^2}+\dfrac{1}{5^2}}+.....+\sqrt{1+\dfrac{1}{2017^2}+\dfrac{1}{2018^2}}\)

Rút gọn : \(\dfrac{\sqrt{45+27\sqrt{2}}+\sqrt{45-27\sqrt{2}}}{\sqrt{5+3\sqrt{2}}-\sqrt{5-3\sqrt{2}}}-\dfrac{\sqrt{3+\sqrt{2}}+\sqrt{3-\sqrt{2}}}{\sqrt{3+\sqrt{2}}-\sqrt{3-\sqrt{2}}}\)

Cho a, b là hai số thực dương thỏa mãn \(a+b\ge4\). Tìm giá trị nhỏ nhất của biểu thức \(P=\dfrac{2a^2+9}{a}+\dfrac{3b^2+2}{b}\)

Cho các số dương a,b thỏa mãn a+2b = 3\(\sqrt{ab}\). Tính tỉ số \(\dfrac{a}{2b}\)

\(\left\{{}\begin{matrix}2\left(x+y\right)+\sqrt{x+1}=4\\2\left(x+y\right)-3\sqrt{x+1}=-5\end{matrix}\right.\)

Tìm min: \(x+2\sqrt{x}+3\)

\(9-4\sqrt{3}\)

tìm tất cả các số nguyên x,y,z thoả mãn

3x² +6y² +2z²+3y²z² - 18 =6

Rút gọn

\(\dfrac{\sqrt{8-2\sqrt{15}}}{\sqrt{10}-\sqrt{6}}\)

Câu hỏi tương tự

Với x, y là các số dương thỏa mãn điều kiện x ≥ 2y . Tìm giá trị nhỏ nhất của biểu thức M = \(\dfrac{x^2+y^2}{xy}\)

trục căn thức ở mẫu
\(\dfrac{13}{\sqrt{3}-2}\) ; \(\dfrac{2-\sqrt{5}}{2+\sqrt{5}}\)

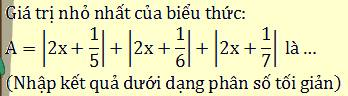
giúp mình nhé!!

tìm x biêt

\(\sqrt{x+2\sqrt{x}-1}-\sqrt{x-2\sqrt{x-1}}=2\)

Rút gọn

a) \(\left(5+4\sqrt{2}\right)\left(3+2\sqrt{1+\sqrt{2}}\right)\left(2-\sqrt{1+\sqrt{2}}\right)\)

b) \(\sqrt{7-2\sqrt{6}-\sqrt{7+2\sqrt{6}}}\)

CÂU 2 :

a, Không dùng máy tính hãy so sánh : \(\dfrac{2014}{\sqrt{2015}}+\dfrac{2015}{\sqrt{2014}}\) và \(\sqrt{2014}+\sqrt{2015}\)

b, Tìm x, y, z biết : \(4x^2+2y^2+2z^2-4xy-2yz+2y-8z+10\le0\)

c, Giair phương trình : \(\sqrt{\dfrac{1}{x+3}}+\sqrt{\dfrac{5}{x+4}}=4\)

tìm giá trị nhỏ nhất của biểu thức:

\(Q=x-2\sqrt{2x-1}\)

Các bạn giải giúp mik với ~~ (nhanh và đúng mình tíck cho :)

a) \(\sqrt{2x}+7\)

b)\(\sqrt{-3x+4}\)

c)\(\sqrt{\dfrac{1}{-1+x}}\)

d)\(\sqrt{1+x^2}\)

Cho a, b, c > 0. CMR: (a + b + c)(ab + bc + ca)(a³ + b³ + c³) \(\le\) (a² + b² + c²)³

Cho các số thực dương a,b,c thỏa mãn a+b+c=6. Chứng minh rằng:

\(\dfrac{b+c+5}{1+a}+\dfrac{c+a+4}{2+b}+\dfrac{a+b+3}{3+c}\ge6\). Dấu đẳng thức xảy ra khi nào ?

\(\sqrt{\left(\sqrt{2}-5\right)^2}\)

Cho a,b,c > 0 và a+b+c <1. Chứng minh rằng: \(\dfrac{1}{a^2+2ab}+\dfrac{1}{b^2+2ac}+\dfrac{1}{c^2+2ab}\ge9\)

Cho x > 1, y > 1. Tìm giá trị nhỏ nhất của biểu thức
\(P=\dfrac{x^2}{y-1}+\dfrac{y^2}{x-1}\)

Tính: \(A=\dfrac{\sqrt{6+2\left(\sqrt{6}+\sqrt{3}+\sqrt{2}\right)}-\sqrt{6-2\left(\sqrt{6}-\sqrt{3}+\sqrt{2}\right)}}{\sqrt{2}}\)

Giải phương trình:
\(\sqrt[3]{x+1}+\sqrt[3]{x+2}+\sqrt[3]{x+3}=0\)

Cho x, y dương.

Tìm giá trị nhỏ nhất của:

\(S=\dfrac{\left(x+y\right)^2}{x^2+y^2}+\dfrac{\left(x+y\right)^2}{xy}\)

giải hệ phương trình sau

\(\left\{{}\begin{matrix}2-\sqrt{x^2y^4+2xy^2-y^4+1}=2\left(3-\sqrt{2}-x\right)y^2\\\sqrt{x-y^2}+x=3\end{matrix}\right.\)

giải phương trình sau \(x^2+2x\sqrt{x-\dfrac{1}{x}}=3x+1\)

Tính giá trị của biểu thức sau :

A=\(\sqrt{53-20\sqrt{4+\sqrt{9-4\sqrt{2}}}}\)

Giải thích cho mình hiểu làm sao để giải biểu thức này với nha

Cho biểu thức \(P=\dfrac{\sqrt{x+2-4\sqrt{x-2}+\sqrt{x+2+4\sqrt{x-2}}}}{2\left(x-2\right)}\) . Rút gọn P

Chứng minh rằng: Nếu a , b, c > 0 thì : \(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{b+a}\ge\dfrac{3}{2}\)

\(\sqrt{3+x}+\sqrt{6-x}=\sqrt{4x^2-12x+27}\)
Giúp mình với >< Giải phương trình

chứng minh
1/căn2+1/căn3+..1/căn225<28

Giải phương trình sau:

\(\sqrt{2-x^2+2x}+\sqrt{-x^2-6x-8}=1+\sqrt{3}\)

Giải phương trình:

a. \(\sqrt{x^2-2x+1}+\sqrt{x^2-6x+9}=1\)

b. \(\sqrt{x+2\sqrt{x-1}}+\sqrt{x-2\sqrt{x-1}}=2\)

c. \(\sqrt{x+3+4\sqrt{x-1}}+\sqrt{x+8+6\sqrt{x-1}}=1\)

Tìm GTNN của bt

\(B=\sqrt{x^2-4x+5}\) và gtrị tương ứng của x

Giải phương trình sau:

a)\(\sqrt{\left(x-3\right)^2}=3-x\) b)\(\sqrt{4x^2-20x+25}+2x=5\)

c)\(\sqrt{1-12x+36x^2}=5\) d)\(\sqrt{x+2\sqrt{x-1}}=2\)

e)\(\sqrt{x-2\sqrt{x-1}}=\sqrt{x-1}-1\) f)\(\sqrt{x^2-\dfrac{1}{2}x+\dfrac{1}{16}}=\dfrac{1}{4}-x\)

Mọi người giúp em với!!!!

Phân tích đa thức sau thành nhân tử:x⁴ + 2009x² +2008 x+2009

Rút gọn

\(\dfrac{5-2\sqrt{5}}{\sqrt{ }5}\)-( \(5\sqrt{5}\) -3)

giải pt( \(\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{1}{a-\sqrt{a}}\)):(\(\dfrac{1}{\sqrt{a}+1}-\dfrac{2}{a-1}\))

\(\sqrt{13+30\sqrt{2+\sqrt{9+4\sqrt{2}}}}\)

1: Dùng máy tính bỏ túi để tìm kết quả của các phép khai chương sau(làm tròn đến chữ số thập phân thứ 2)

a, \(\sqrt{10}\) ; b, \(\sqrt{29}\) ; c, \(\sqrt{107}\) ; d, \(\sqrt{19,7}\)

2: Tìm số x không âm , biết :

a, \(\sqrt{x}>1\) ; b, \(\sqrt{x}< 3\) ; c, \(2\sqrt{x}=14\)

Mẫu : với x ≥ 0, ta có \(\sqrt{x}>1\) ⇔ \(\sqrt{x}>\sqrt{1}\) ⇔ x>1. Vậy x>1

Tìm giá trị lớn nhất của biểu thức P = \(\sqrt{x-5}+\sqrt{13-x}\)

Cho x;y thoả mãn điều kiện : \(\sqrt{x+2}-y^3=\sqrt{y+2}-x^3\)

Tìm giá trị nhỏ nhất của biểu thức \(A=x^2+2xy-2y^2+2y+10\)

T.Thùy Ninh [tag cho có thông báo thoy ạ....:3 ]

Giúp tớ vs ạ ...Càng học càng ngu bmr

1: Chọn các câu trả lời đúng:

\(\sqrt{121=11}\) ; \(\sqrt{144=12}\) ; \(\sqrt{6400=12}\) ; \(\sqrt{0,49=-0,7}\) ; \(\sqrt{\dfrac{49}{9}}=\dfrac{7}{3}\) ; \(\sqrt{0,01=-0,1}\)

2: So sánh:

a, 6 và \(\sqrt{37}\) ; b, \(\sqrt{17}\) và 4 ; c, \(\sqrt{0,7}\) và 0,8

3. Đúng ghi Đ, sai ghi S.

a, 3< \(\sqrt{10}\)<4 ; b, 1,1 < \(\sqrt{1,56}\)<1,2

Mọi người giúp e với e cảm ơn ạ

Tìm tất cả các số có 2 chữ số có dạng \(\overline{ab}^2-\overline{ba}^2=1980\)

*tớ chỉ muốn hỏi là bài này làm có ra không và ra bao nhiêu nhé, đưng giải, cảm ơn nhiều nhiều!!

1/ giai phuong trinh : \(\sqrt{\dfrac{2x+2}{x+2}}-\sqrt{\dfrac{x+2}{2x+2}}=\dfrac{7}{12}\)

2/ cho tam giac ABC vuong tai A, phan giac AD;AE.

a/ chung minh \(\dfrac{\sqrt{2}}{AD}=\dfrac{1}{AB}+\dfrac{1}{AC}\)

b/ he thuc tren thay doi nhu the nao neu BAC=60^o ? BAC=120^o

c/ he thuc tren thay doi nhu the nao neu thay doi phan giac trong AD voi phan giac ngoai AE

Tim GTNN

A=4X²-X-2

B= \(\dfrac{2X^2+6X-3}{5}\)

C= X⁴+4X-1

D= 4X²+\(\dfrac{9}{X^2}\) với x khác 0

cho 3 số a,b,c >0

CMR:\(\dfrac{a^3}{a^2+b^2}+\dfrac{b^3}{b^2+c^2}+\dfrac{c^3}{c^2+a^2}\ge\dfrac{a+b+c}{2}\)

Cho a;b;c;d>0 thỏa mãn: a+b+c+d=4. Tìm min của:

\(\sqrt{a^2+\dfrac{1}{b^2}}+\sqrt{b^2+\dfrac{1}{c^2}}+\sqrt{c^2+\dfrac{1}{d^2}}+\sqrt{d^2+\dfrac{1}{a^2}}\)

rút gọn

P = \(\left(\dfrac{1}{\sqrt{x}+2}+\dfrac{1}{\sqrt{x}-2}\right):\dfrac{\sqrt{x}}{x-4}\) với x > 0, x \(\ne\) 4

TÌm nghiệm nguyên x,y của phương trình \(x^2y^2-xy=x^2+2y^2\)

Mình bik làm bài này r nhưng dài quá

Cok ai giúp mik cách khác dc k

Cho các số dương a,b,c thỏa mãn a+b+c=abc . tìm giá trị lớn nhất của bt

\(S=\dfrac{a}{\sqrt{bc\left(1+a^2\right)}}+\dfrac{b}{\sqrt{ca\left(1+b^2\right)}}+\dfrac{c}{\sqrt{ab\left(1+c^2\right)}}\)

\(\sqrt{\left(x-2\right)^2+9}\ge3\)

Cho x>0, y>0 thỏa mãn \(x+y\ge5\). Tìm giá trị nhỏ nhất của biểu thức: \(P=4x+3y+\dfrac{6}{x}+\dfrac{9}{2y}\)

giải phương trình:

\(\sqrt{3}x^2-\sqrt{12}=0\)

tìm gtnn của biểu thức

\(\dfrac{x^2+x+1}{x^2+2x+2}\)

chứng minh vô nghiệm

\(\dfrac{x^2+2+\sqrt{x^2+1}}{\sqrt{x^2+1}+1}+3x^2-4x=0\)

rút gọn căn thức

\(x+2y-\sqrt{\left(x^2-4xy+4y^2\right)\left(x\ge2y\right)}\)

Tìm x để căn thức có nghĩa:

a) \(\sqrt{\left(x-1\right)}.\sqrt{\left(x-3\right)}\)

b) \(\sqrt{\left(x-4\right)\left(x+2\right)}\)

rút gọn biểu thức

\(\dfrac{2+\sqrt{2}}{1+\sqrt{2}}\)

Nghiệm của phương trình : \(\sqrt{x^2-3x+3}=1\)

TÍNH :
( 3 + \(\sqrt{5}\)) . ( \(\sqrt{10}-\sqrt{2}\)) . \(\sqrt{3-\sqrt{ }5}\)

nghiệm của phương trình :\(\sqrt{\left(x-1\right)^2=1}\)

Cho các số dương a,b,c CMR

\(\frac{a^4}{b^3(c+2a)}+\frac{b^4}{c^3(a+2b)}+\frac{c^4}{a^3(b+2c)}\ge 1\)

@Akai Haruma

gpt : \(\sqrt{\dfrac{x^2-2x+1}{x^2-6+9}}=0\)

P=\(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}-\dfrac{2+5\sqrt{x}}{x-4}\)

Tìm x để P=2

giải phương trình :
\(\sqrt{x-2}+2\cdot\sqrt{x-3}+\sqrt{x+6+6\cdot\sqrt{x-3}}=4\)

\(\dfrac{\sqrt{3-\sqrt{5}}\left(3+\sqrt{5}\right)}{\sqrt{10}+\sqrt{2}}\)

Giải phương trình \(\sqrt{2x+1}+\frac{2x-1}{x+3}-(2x-1)\sqrt{x^2+4}-\sqrt{2}=0\)

1) Thực hiện phép tính

a) \(\sqrt{\dfrac{25}{7}}.\sqrt{\dfrac{7}{9}}\)

b) ( \(\sqrt{\dfrac{9}{2}}+\sqrt{\dfrac{1}{2}}-\sqrt{2}\) ) . \(\sqrt{2}\)

c) ( \(\sqrt{\dfrac{8}{3}}-\sqrt{24}+\sqrt{\dfrac{50}{3}}\)) . \(\sqrt{6}\)

d) (\(\sqrt{\dfrac{2}{3}}-\sqrt{\dfrac{3}{2}}\))\(^2\)

2) Rút gọn các biểu thức

a) \(\sqrt{4+2\sqrt{3}}\)

b) \(\sqrt{8-2\sqrt{7}}\)

c) \(1+\sqrt{6-2\sqrt{5}}\)

d) \(\sqrt{7-2\sqrt{10}}+\sqrt{2}\)

3) Tính giá trị của biểu thức

a) A = x\(^2\)+2x + 16 với x = \(\sqrt{2}\)- 1

b) B = x\(^2\)+12x - 14 với x = \(5\sqrt{2}-6\)

Rút gọn:

A=\(\sqrt{6+2\sqrt{2}.\sqrt{3-\sqrt{4+2\sqrt{3}}}}\)

Tìm x :

a, \(x=\sqrt{6}\)

b, \(x=-\sqrt{14}\)

c, \(x=2\sqrt{3}\)

Tìm x để căn thức có nghĩa:

a) \(\sqrt{-5x}\)

b) \(\sqrt{4-x}\)

c) \(\sqrt{3x+7}\)

d) \(\dfrac{2}{x^2}\)

e) \(\sqrt{\sqrt{x-3}-2}\)

c) \(\dfrac{4-x}{x^2-25}+\sqrt{-x-7}\)

Cho x + y=15. Tìm GTNN, GTLN của biểu thức A= \(\sqrt{x-4}+\sqrt{y-3}\)

Giải bất phương trình sau:

c) (2015+x)(x−5)>0

d) \(\dfrac{5-6x}{x+2}>0\)

cho a>0. tìm giá trị nhỏ nhất của biểu thức sau P=\(\dfrac{2a^2+3a+8}{a}\)

Cho a,b,c là các số thực dương.Tìm giá trị nhỏ nhất của

\(P=\dfrac{\left(a+b+c\right)^2}{30\left(a^2+b^2+c^2\right)}+\dfrac{a^3+b^3+c^3}{4abc}-\dfrac{131\left(a^2+b^2+c^2\right)}{60\left(ab+bc+ca\right)}\)

cho a,b,c,d \(\ge0\) cmr:
a+b+\(\dfrac{1}{2}\ge\sqrt{a}+\sqrt{b}\)

giúp mk vs nhé

*Tìm số dư của phép chia:

3¹¹⁸¹ cho 28

2009²⁰¹⁰ cho 2011

97²⁰⁰²¹ cho 51

*Chứng minh rằng :

2²⁰⁰² - 4 chia hết cho 31

\(\dfrac{\sqrt{21}-\sqrt{7}}{1-\sqrt{3}}\)

ai giúp e với !

Tìm tất cả các số nguyên n sao cho A = (n-2010)(n-2011)(n-2012) là số chính phương

cho a,b,c là số thực dương, tìm Max: \(\sqrt{\dfrac{a}{b+c+2a}}+\sqrt{\dfrac{b}{c+a+2b}}+\sqrt{\dfrac{c}{a+b+2c}}\)

Bài tập: Thực hiện phép tính

a. \(\sqrt{27}-3\sqrt{48}+2\sqrt{108}-\sqrt{\left(2-\sqrt{3}\right)^2}\)

b. \(3\sqrt{2}\left(\sqrt{50}-2\sqrt{18}+\sqrt{98}\right)\)

Bài 1/ P=\(\dfrac{15\sqrt{x}-11}{x+2\sqrt{x}-3}+\dfrac{3\sqrt{x}-2}{1-\sqrt{x}}-\dfrac{2\sqrt{x}+3}{\sqrt{x}+3}\)

a/ Rút gọn

b/ Tìm x để P=\(\dfrac{1}{2}\)

c/ Chứng minh P _< \(\dfrac{2}{3}\)

Giúp em vs ạ

Nhanh nha mn

giải pt \(\sqrt{x+2-3\sqrt{2x-5}}+\sqrt{x-2+\sqrt{2x-5}}=2\sqrt{2}\)

Phân tích: a, 3x\(^2\)-7x+2

b, (x+2)(x+3)(x+4)(x+5)-24

c, x\(^4\)+4

C=\(\sqrt{\left(\sqrt{5+2}\right)^2}-\sqrt{5}\)

D=\(\sqrt{8}+\sqrt{18}-\sqrt{32}\)

E=\(\sqrt{9-4\sqrt{5}}-\sqrt{5}\)

F=\(2\sqrt{8}-\sqrt{50}+\sqrt{\left(\sqrt{2}+1\right)^2}\)

Rút gọn : C= \(\left(\dfrac{x-5\sqrt{x}}{x-25}-1\right):\left(\dfrac{25-x}{x+2\sqrt{x}-15}-\dfrac{\sqrt{x}+3}{\sqrt{x}+5}+\dfrac{\sqrt{x}-5}{\sqrt{x}-3}\right)\)

Rút gọn

A=\(3\sqrt{3}-2\sqrt{12}-27\)

B= \(\sqrt{\left(3-\sqrt{5}\right)^2}+\sqrt{6-2\sqrt{5}}\)

giải hương trình \(\sqrt{3x^2+5x+8}trừ\sqrt{3x^2+5x+1}=1\)

Giải:

\(\left\{{}\begin{matrix}3\sqrt{x-2}-\sqrt{y+2}=1\\\sqrt{x-2}+\sqrt{y+2}=3\end{matrix}\right.\)

Hãy so sánh hai biểu thức sau:

\(x=\dfrac{2+\sqrt{3}}{\sqrt{2}+\sqrt{2+\sqrt{3}}}+\dfrac{2-\sqrt{3}}{\sqrt{2}-\sqrt{2-\sqrt{3}}}\)

\(y=\dfrac{3+\sqrt{5}}{\sqrt{10}+\sqrt{3+\sqrt{5}}}-\dfrac{3-\sqrt{5}}{\sqrt{10}+\sqrt{3-\sqrt{5}}}\)

TÌM GTNN GIÚP

2x+8νx−2

Tìm các cặp số nguyên (x;y) thỏa mãn điều kiện x² - 4xy + 5y² = 2(x - y)

cho A=\(\dfrac{1}{1+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+......+\dfrac{1}{\sqrt{20}+\sqrt{21}}\)

\(\sqrt{3x^2-5x+1}-\sqrt{x^2-2}=\sqrt{3\left(x^2-x-1\right)}-\sqrt{x^2-3x+4}\)

Bài tập: Tìm giá trị lớn nhất của biểu thức \(A=4-\sqrt{x^2-4x+4}\)

cho a,b,c ≥0. CMR:

a+b+\(\dfrac{1}{2}\ge\sqrt{a}+\sqrt{b}\)

Bài tập: Tìm x biết

a. \(\sqrt{x}=x\)

b. \(\sqrt{2x-4}=2\)

cho a,b,b ≥0. Chứng minh rằng:

\(\dfrac{a+b}{2}\ge\sqrt{ab}\)

Bài tập: Phân tích ra thừa số

\(\sqrt{xy}+1+\sqrt{x}+\sqrt{y}\) \(\left(x,y>0\right)\)

Cho x, y, z > 0 thỏa mãn \(x+y+z\le3\).Tìm GTLN :

\(A=\sqrt{1+x^2}+\sqrt{1+y^2}+\sqrt{1+z^2}+2\left(\sqrt{x}+\sqrt{y}+\sqrt{z}\right)\)

Rút gọn H=\((\dfrac{x-\sqrt{x}+2}{x-\sqrt{x}-2}-\dfrac{x}{x-2\sqrt{x}}):\dfrac{1-\sqrt{x}}{2-\sqrt{x}}\)

a)\(\sqrt{x+3-4\sqrt{x-1}}+\sqrt{x+8-6\sqrt{x-1}}=1\)

b) \(\left|\sqrt{x-1}-2\right|+\left|\sqrt{x-1}+3\right|\ge5\)