Giải bài 1.53 tr 43 SBT Hình học 10
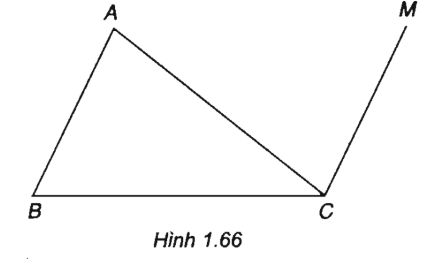
Cho tam giác \(ABC\). Tìm điểm \(M\) thỏa mãn điều kiện \(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \).
Hướng dẫn giải chi tiết
\(\overrightarrow {MA} - \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \)\( \Leftrightarrow \overrightarrow {BA} = - \overrightarrow {MC} \Leftrightarrow \overrightarrow {BA} = \overrightarrow {CM} \).
Vậy \(M\) là đỉnh của hình bình hành \(ABCM\).
-- Mod Toán 10 HỌC247
-


Cho tam giác ABC vuông tại A có AB=6, AC=8. Độ dài của véctơ \(\overrightarrow {BA} + \overrightarrow {BC} \) là:
bởi can tu
 19/02/2021
19/02/2021
A.\(2\sqrt 3 \)
B.10
C.\(4\sqrt {13} \)
D.16
Theo dõi (0) 1 Trả lời -


Cho tam giác đều ABC có cạnh bằng a. Độ dài của véctơ \(\overrightarrow {BA} + \overrightarrow {BC} \) là"
bởi Nguyễn Hiền
 20/02/2021
20/02/2021
A. 2a
B. \({{a\sqrt 3 } \over 2}\)
C. a
D. \(a\sqrt 3 \)
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC và một đường thẳng \(\Delta \). Tìm trên \(\Delta \) điểm M sao cho véctơ \(2\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} \)có độ dài ngắn nhất.
bởi Mai Linh
 19/02/2021
Theo dõi (0) 1 Trả lời
19/02/2021
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại B có trọng tâm là G. Biết rằng \(AB = 3\) và \(AC = 5\). Tính độ dài của các véctơ \(\overrightarrow {GB} - \overrightarrow {GC} \) và \(\overrightarrow {GB} + \overrightarrow {GC} \).
bởi Hồng Hạnh
 20/02/2021
Theo dõi (0) 1 Trả lời
20/02/2021
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 1.51 trang 43 SBT Hình học 10
Bài tập 1.52 trang 43 SBT Hình học 10
Bài tập 1.54 trang 43 SBT Hình học 10
Bài tập 1.55 trang 43 SBT Hình học 10
Bài tập 1.56 trang 43 SBT Hình học 10
Bài tập 1.57 trang 44 SBT Hình học 10
Bài tập 1.58 trang 44 SBT Hình học 10
Bài tập 1.59 trang 44 SBT Hình học 10
Bài tập 1.60 trang 44 SBT Hình học 10
Bài tập 1.61 trang 44 SBT Hình học 10
Bài tập 1.62 trang 44 SBT Hình học 10
Bài tập 1.63 trang 44 SBT Hình học 10
Bài tập 1.64 trang 45 SBT Hình học 10
Bài tập 1.65 trang 45 SBT Hình học 10
Bài tập 1.66 trang 45 SBT Hình học 10
Bài tập 1.67 trang 45 SBT Hình học 10
Bài tập 1.68 trang 45 SBT Hình học 10
Bài tập 1.69 trang 45 SBT Hình học 10
Bài tập 1.70 trang 45 SBT Hình học 10
Bài tập 1.71 trang 46 SBT Hình học 10
Bài tập 1.72 trang 46 SBT Hình học 10
Bài tập 1.73 trang 46 SBT Hình học 10
Bài tập 1.74 trang 46 SBT Hình học 10
Bài tập 1.75 trang 46 SBT Hình học 10
Bài tập 1.76 trang 46 SBT Hình học 10
Bài tập 1.77 trang 46 SBT Hình học 10
Bài tập 1.78 trang 46 SBT Hình học 10
Bài tập 1.79 trang 47 SBT Hình học 10
Bài tập 1.80 trang 47 SBT Hình học 10
Bài tập 1.81 trang 47 SBT Hình học 10
Bài tập 1.82 trang 47 SBT Hình học 10
Bài tập 1.83 trang 47 SBT Hình học 10
Bài tập 1.84 trang 48 SBT Hình học 10
Bài tập 1.85 trang 47 SBT Hình học 10
Bài tập 1.86 trang 48 SBT Hình học 10
Bài tập 1.87 trang 48 SBT Hình học 10
Bài tập 1.88 trang 48 SBT Hình học 10
Bài tập 1.89 trang 49 SBT Hình học 10
Bài tập 1.90 trang 49 SBT Hình học 10
Bài tập 1.91 trang 49 SBT Hình học 10
Bài tập 1.92 trang 49 SBT Hình học 10
Bài tập 1.93 trang 49 SBT Hình học 10
Bài tập 1.95 trang 49 SBT Hình học 10
Bài tập 1.96 trang 49 SBT Hình học 10
Bài tập 1.97 trang 50 SBT Hình học 10
Bài tập 1.98 trang 50 SBT Hình học 10
Bài tập 1.99 trang 50 SBT Hình học 10
Bài tập 1.100 trang 50 SBT Hình học 10
Bài tập 1 trang 34 SGK Hình học 10 NC
Bài tập 2 trang 34 SGK Hình học 10 NC
Bài tập 3 trang 34 SGK Hình học 10 NC
Bài tập 4 trang 34 SGK Hình học 12 NC
Bài tập 5 trang 35 SGK Hình học 12 NC
Bài tập 6 trang 35 SGK Hình học 12 NC
Bài tập 7 trang 36 SGK Hình học 10 NC
Bài tập 8 trang 36 SGK Hình học10 NC
Bài tập 9 trang 36 SGK Hình học 10 NC
Bài tập 10 trang 36 SGK Hình học 10 NC
Bài tập 11 trang 36 SGK Hình học 10 NC
Bài tập 12 trang 37 SGK Hình học 10 NC
Bài tập 13 trang 37 SGK Hình học 10 NC
Bài tập 14 trang 37 SGK Hình học 10 NC
Bài tập 15 trang 37 SGK Hình học 10 NC
Bài tập 16 trang 37 SGK Hình học 10 NC
Bài tập 17 trang 37 SGK Hình học 10 NC
Bài tập 18 trang 37 SGK Hình học 10 NC
Bài tập 19 trang 38 SGK Hình học 10 NC
Bài tập 20 trang 38 SGK Hình học 10 NC
Bài tập 21 trang 38 SGK Hình học 10 NC