Giải bài 1.66 tr 45 SBT Hình học 10
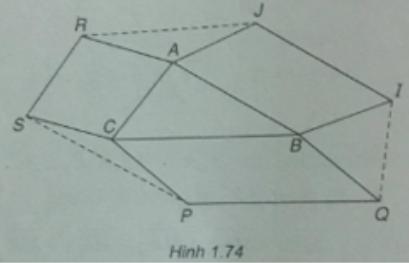
Cho tam giác ABC. Bên ngoài của tam giác vẽ các hình bình hành ABIJ, BCPQ, CARS. Chứng minh rằng:
\(\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \overrightarrow 0 \)
Hướng dẫn giải chi tiết
\(\begin{array}{l}
\overrightarrow {RJ} + \overrightarrow {IQ} + \overrightarrow {PS} = \overrightarrow {RA} + \overrightarrow {AJ} + \overrightarrow {IB} + \overrightarrow {BQ} + \overrightarrow {PC} + \overrightarrow {CS} \\
= \left( {\overrightarrow {RA} + \overrightarrow {CS} } \right) + \left( {\overrightarrow {AJ} + \overrightarrow {IB} } \right) + \left( {\overrightarrow {BQ} + \overrightarrow {PC} } \right) = \overrightarrow 0
\end{array}\)
-- Mod Toán 10 HỌC247
-


Chứng minh vtAB+vtCD+vtEA=vtCB+vtED
bởi Thư Võ
 02/12/2019
02/12/2019
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Đẳng thức nào thể hiện đúng hình vẽ sau?
bởi phạm ánh
 11/11/2019
Giúp hộ câu 33 và36
11/11/2019
Giúp hộ câu 33 và36 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tính độ dài vtAB-vtBC biết tam giác ABC vuông cân tại A
bởi Ánh Ngọc
 10/11/2019
10/11/2019
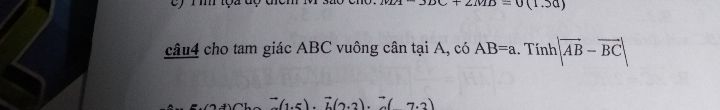 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


Đẳng thức nào dưới đây đúng?
bởi Huyen Duong
 07/11/2019
Giúp mình câu tô đỏ với
07/11/2019
Giúp mình câu tô đỏ với Theo dõi (1) 1 Trả lời
Theo dõi (1) 1 Trả lời
Bài tập SGK khác
Bài tập 1.64 trang 45 SBT Hình học 10
Bài tập 1.65 trang 45 SBT Hình học 10
Bài tập 1.67 trang 45 SBT Hình học 10
Bài tập 1.68 trang 45 SBT Hình học 10
Bài tập 1.69 trang 45 SBT Hình học 10
Bài tập 1.70 trang 45 SBT Hình học 10
Bài tập 1.71 trang 46 SBT Hình học 10
Bài tập 1.72 trang 46 SBT Hình học 10
Bài tập 1.73 trang 46 SBT Hình học 10
Bài tập 1.74 trang 46 SBT Hình học 10
Bài tập 1.75 trang 46 SBT Hình học 10
Bài tập 1.76 trang 46 SBT Hình học 10
Bài tập 1.77 trang 46 SBT Hình học 10
Bài tập 1.78 trang 46 SBT Hình học 10
Bài tập 1.79 trang 47 SBT Hình học 10
Bài tập 1.80 trang 47 SBT Hình học 10
Bài tập 1.81 trang 47 SBT Hình học 10
Bài tập 1.82 trang 47 SBT Hình học 10
Bài tập 1.83 trang 47 SBT Hình học 10
Bài tập 1.84 trang 48 SBT Hình học 10
Bài tập 1.85 trang 47 SBT Hình học 10
Bài tập 1.86 trang 48 SBT Hình học 10
Bài tập 1.87 trang 48 SBT Hình học 10
Bài tập 1.88 trang 48 SBT Hình học 10
Bài tập 1.89 trang 49 SBT Hình học 10
Bài tập 1.90 trang 49 SBT Hình học 10
Bài tập 1.91 trang 49 SBT Hình học 10
Bài tập 1.92 trang 49 SBT Hình học 10
Bài tập 1.93 trang 49 SBT Hình học 10
Bài tập 1.95 trang 49 SBT Hình học 10
Bài tập 1.96 trang 49 SBT Hình học 10
Bài tập 1.97 trang 50 SBT Hình học 10
Bài tập 1.98 trang 50 SBT Hình học 10
Bài tập 1.99 trang 50 SBT Hình học 10
Bài tập 1.100 trang 50 SBT Hình học 10
Bài tập 1 trang 34 SGK Hình học 10 NC
Bài tập 2 trang 34 SGK Hình học 10 NC
Bài tập 3 trang 34 SGK Hình học 10 NC
Bài tập 4 trang 34 SGK Hình học 12 NC
Bài tập 5 trang 35 SGK Hình học 12 NC
Bài tập 6 trang 35 SGK Hình học 12 NC
Bài tập 7 trang 36 SGK Hình học 10 NC
Bài tập 8 trang 36 SGK Hình học10 NC
Bài tập 9 trang 36 SGK Hình học 10 NC
Bài tập 10 trang 36 SGK Hình học 10 NC
Bài tập 11 trang 36 SGK Hình học 10 NC
Bài tập 12 trang 37 SGK Hình học 10 NC
Bài tập 13 trang 37 SGK Hình học 10 NC
Bài tập 14 trang 37 SGK Hình học 10 NC
Bài tập 15 trang 37 SGK Hình học 10 NC
Bài tập 16 trang 37 SGK Hình học 10 NC
Bài tập 17 trang 37 SGK Hình học 10 NC
Bài tập 18 trang 37 SGK Hình học 10 NC
Bài tập 19 trang 38 SGK Hình học 10 NC
Bài tập 20 trang 38 SGK Hình học 10 NC
Bài tập 21 trang 38 SGK Hình học 10 NC