Giải bài 1.70 tr 45 SBT Hình học 10
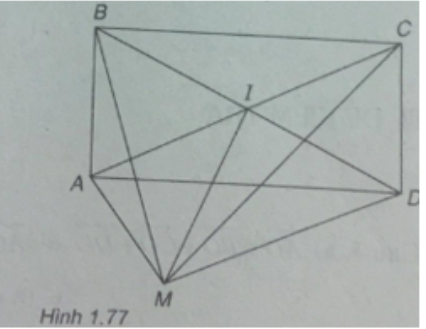
Cho hình chữ nhật ABCD. Gọi I là giao điểm của hai đường chéo AC và BD.
a) Với điểm M tùy ý, hãy chứng minh:
\(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \)
b) Chứng minh rằng \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB} - \overrightarrow {AD} } \right|\)
Hướng dẫn giải chi tiết
a) \(\left. \begin{array}{l}
\overrightarrow {MA} + \overrightarrow {MC} = 2\overrightarrow {MI} \\
\overrightarrow {MB} + \overrightarrow {MD} = 2\overrightarrow {MI}
\end{array} \right\} \Rightarrow \overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MB} + \overrightarrow {MD} \)
b) Ta có:
\(\begin{array}{l}
\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \Leftrightarrow \left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AC} } \right| = AC\\
\overrightarrow {AB} - \overrightarrow {AD} = \overrightarrow {DB} \Rightarrow \left| {\overrightarrow {AB} - \overrightarrow {AD} } \right| = DB
\end{array}\)
Vì hai đường chéo của hình chữ nhật dài bằng nhau nên \(\left| {\overrightarrow {AB} + \overrightarrow {AD} } \right| = \left| {\overrightarrow {AB} - \overrightarrow {AD} } \right|\)
-- Mod Toán 10 HỌC247
-
Chứng minh 3 điểm C,I,K thẳng hàng biết I, K là trung điểm AG và AB
bởi Nguyễn Phương Khanh
05/11/2018
Cho tam giac ABC vs trọng tâm G.Gọi I la trung diem của doan AG va K la diem tren cạnh AB sao cho AK=1/5 AB
a/ hay phan tich AI,AK,CI,CK theo vecto a= vecto CA,veto b =vecto CB
b/ c/m 3 điểm C,I,K thang hàng
Theo dõi (0) 1 Trả lời -
Cho tam giác ABC với A(2; 5), B(1; 1), C(3; 3). Tìm tọa độ điểm D để ABCD là hình bình hành. Tìm tọa độ tâm hình bình hành đó
Theo dõi (0) 1 Trả lời
