Bài tập 8 trang 36 SGK Hình học10 NC
Cho hình thang \(ABCD\) với hai cạnh đáy là \(AB = 3a\) và \(CD = 6a\). Khi đó \(\left| {\overrightarrow {AB} + \overrightarrow {CD} } \right|\) bằng bao nhiêu ?
(A) \(9a\)
(B) \(3a\)
(C) \(-3a\)
(D) \(0\).
Hướng dẫn giải chi tiết
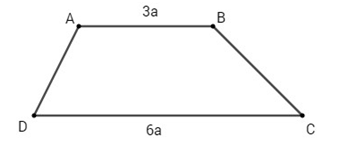
Gọi \(E\) là trung điểm \(CD\). Ta có:
\(\left| {\overrightarrow {AB} + \overrightarrow {CD} } \right| = \left| {\overrightarrow {DE} + \overrightarrow {CD} } \right|\)
\( = \left| {\overrightarrow {CD} + \overrightarrow {DE} } \right|\)
\(= \left| {\overrightarrow {CE} } \right| = CE = 3a.\)
Chọn (B).
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.
Bài tập SGK khác
Bài tập 6 trang 35 SGK Hình học 12 NC
Bài tập 7 trang 36 SGK Hình học 10 NC
Bài tập 9 trang 36 SGK Hình học 10 NC
Bài tập 10 trang 36 SGK Hình học 10 NC
Bài tập 11 trang 36 SGK Hình học 10 NC
Bài tập 12 trang 37 SGK Hình học 10 NC
Bài tập 13 trang 37 SGK Hình học 10 NC
Bài tập 14 trang 37 SGK Hình học 10 NC
Bài tập 15 trang 37 SGK Hình học 10 NC
Bài tập 16 trang 37 SGK Hình học 10 NC
Bài tập 17 trang 37 SGK Hình học 10 NC
Bài tập 18 trang 37 SGK Hình học 10 NC
Bài tập 19 trang 38 SGK Hình học 10 NC
Bài tập 20 trang 38 SGK Hình học 10 NC
Bài tập 21 trang 38 SGK Hình học 10 NC





