Giải bài 1.71 tr 46 SBT Hình học 10
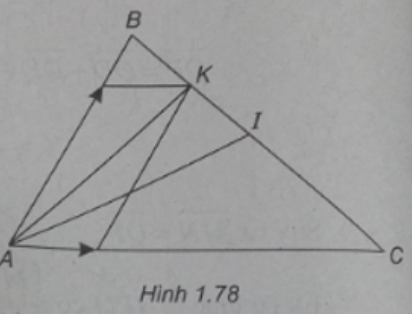
Cho tam giác ABC. Gọi I là trung điểm của BC, K là trung điểm của BI.
Chứng minh rằng:
a) \(\overrightarrow {AK} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AI} \)
b) \(\overrightarrow {AK} = \frac{3}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC} \)
Hướng dẫn giải chi tiết
a) Vì K là trung điểm của BI nên\(\overrightarrow {AK} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AI} } \right) = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AI} \) (1)
b) Vì I là trung điểm của BC nên \(\overrightarrow {AI} = \frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)\) (2)
Thay (2) vào (1) ta được:
\(\overrightarrow {AK} = \frac{3}{4}\overrightarrow {AB} + \frac{1}{4}\overrightarrow {AC} \)
-- Mod Toán 10 HỌC247
-
cho hình bình hành ABCD tâm O . 2 đ' M và N di động sao cho \(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}\) .cmr MN luôn đi qua 1 đ' cố định
Theo dõi (0) 1 Trả lời -
cho lục giác đều ABCDEF có tâm O . chứng minh rằng :
a, \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}+\overrightarrow{OE}+\overrightarrow{OF}=\overrightarrow{O}\)
b, \(\overrightarrow{OA}+\overrightarrow{OC}+\overrightarrow{OE}=\overrightarrow{O}\)
c, \(\overrightarrow{AB}+\overrightarrow{AO}+\overrightarrow{AF}=\overrightarrow{AD}\)
d, \(\overrightarrow{MA}+\overrightarrow{MC}+\overrightarrow{ME}=\overrightarrow{MB}+\overrightarrow{MD}+\overrightarrow{MF}\) (M tùy ý )
Theo dõi (0) 1 Trả lời
