Giải bài 1.58 tr 44 SBT Hình học 10
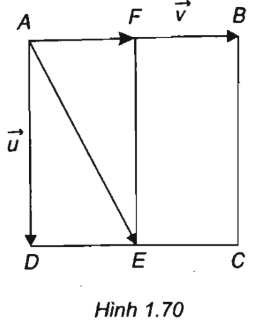
Cho hình vuông ABCD, E là trung điểm của CD. Hãy phân tích \(\overrightarrow {AE} \) theo hai vec tơ \(\overrightarrow u = \overrightarrow {AD} ,\overrightarrow v = \overrightarrow {AB} \).
Hướng dẫn giải chi tiết
Gọi F là trung điểm của cạnh AB.
Ta có: \(\overrightarrow {AE} = \overrightarrow {AD} + \overrightarrow {AF} = \overrightarrow u + \frac{1}{2}\overrightarrow v \)
Vậy \(\overrightarrow {AE} = \overrightarrow u + \frac{1}{2}\overrightarrow v \)
-- Mod Toán 10 HỌC247
-
Đề kiểm tra số 1 - Câu 1 (SBT trang 48)Cho hình bình hành ABCD có hai đường chéo cắt nhau tại O. Hãy thực hiện các phép toán sau :
a) \(\overrightarrow{AO}+\overrightarrow{BO}+\overrightarrow{CO}+\overrightarrow{DO}\)
b) \(\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AC}\)
c) \(\overrightarrow{OC}-\overrightarrow{OD}\)
Theo dõi (0) 1 Trả lời -
Bài 1.71 - Đề toán tổng hợp (SBT trang 48)Cho tam giác. Gọi I là trung điểm của BC, K là trung điểm của BI. Chứng minh rằng :
a) \(\overrightarrow{AK}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AI}\)
b) \(\overrightarrow{AK}=\dfrac{3}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}\)
Theo dõi (0) 1 Trả lời
