Giải bài 2 tr 99 sách GK Toán Hình lớp 12
Cho khối lập phương ABCD.A'B'C'D' cạnh a. Gọi E và F lần lượt là trung điểm B'C' và C'D'. Mặt phẳng (AEF) chia khối lập phương đó thành hai khối đa diện (H) và (H') trong đó (H) là khối đa diện chứa đỉnh A'. Tính thể tích của (H).
Hướng dẫn giải chi tiết bài 2
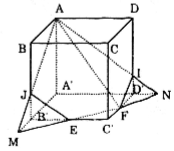
Đường thẳng EF cắt A'B' và A'D' lần lượt tại M và N.
Gọi I là giao điểm của AN và DD', J là giao điểm của AM và BB'.
Mặt phẳng (AEF) cắt hình lập phương theo thiết diện là ngũ giác AIFEJ.
Ta có \(MB'=ND'=\frac{a}{2}\)
Do đó \(\frac{ID'}{ID}=\frac{D'N}{DA}=\frac{1}{2}\Rightarrow ID'=\frac{a}{3}\)
Tương tự: \(JB'=\frac{a}{3}\)
Ta có: \(V_{J.B'ME}=V_{I.D'NF}=\frac{1}{3}.\frac{1}{2}.\frac{a^2}{4}.\frac{a}{3}=\frac{a^3}{72}\)
\(V_{A.A'MN}=\frac{1}{3}.\frac{1}{2}.\frac{9a^2}{4}.a=\frac{3a^3}{8}\)
Tử đó suy ra:
\(V_H=V_{A.A'MN}=-V_{J.B'ME}-V_{I.D'NF}=\frac{3a^3}{8}-2.\frac{a^3}{72}= \frac{25}{72}a^3\)
-- Mod Toán 12 HỌC247
-


Trong không gian với hệ tọa độ \(Oxyz\), biết rằng tập hợp tất cả các điểm \(M\left( {x;y;z} \right)\) sao cho \(\left| x \right| + \left| y \right| + \left| z \right| = 3\) là một hình đa diện. Tính thể tích V của khối đa diện đó.
bởi Truc Ly
 07/07/2022
07/07/2022
A. \(V = 72\).
B. \(V = 36\).
C. \(V = 27\).
D. \(V = 54\).
Theo dõi (0) 1 Trả lời -


Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng a. Diện tích S của mặt cầu ngoại tiếp hình lập phương đó là:
bởi Mai Hoa
 08/07/2022
08/07/2022
A. \(S = \pi {a^2}\).
B. \(S = \dfrac{{3\pi {a^2}}}{4}\).
C. \(S = 3\pi {a^2}\).
D. \(S = 12\pi {a^2}\).
Theo dõi (0) 1 Trả lời -


Trong không gian với hệ tọa độ \(Oxyz\), cho \(A\left( { - 3;0;0} \right),\,B\left( {0;0;3} \right),C\left( {0; - 3;0} \right)\). Điểm \(M\left( {a;b;c} \right)\) nằm trên mặt phẳng \(Oxy\) sao cho \(M{A^2} + M{B^2} - M{C^2}\) nhỏ nhất. Tính \({a^2} + {b^2} - {c^2}\).
bởi can chu
 08/07/2022
08/07/2022
A. 18
B. 0
C. 9
D. -9
Theo dõi (0) 1 Trả lời -


Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông tâm O cạnh a, SO vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và \(SO = a\). Khoảng cách giữa \(SC\) và \(AB\) bằng
bởi Bùi Anh Tuấn
 08/07/2022
08/07/2022
A. \(\dfrac{{a\sqrt 5 }}{5}\).
B. \(\dfrac{{a\sqrt 3 }}{{15}}\).
C. \(\dfrac{{2a\sqrt 5 }}{5}\).
D. \(\dfrac{{2a\sqrt 3 }}{{15}}\).
Theo dõi (0) 1 Trả lời -


Cho hình chóp \(O.\,ABC\) có ba cạnh \(OA,\,OB,\,OC\) đôi một vuông góc và \(OA = OB = OC = a\). Gọi \(M\) là trung điểm cạnh \(AB\). Góc hợp bởi hai véc tơ \(\overrightarrow {BC} \) và \(\overrightarrow {OM} \) bằng
bởi thúy ngọc
 08/07/2022
08/07/2022
A \(120^0\)
B. \(150^0\)
C. \(135^0\)
D. \(60^0\)
Theo dõi (0) 1 Trả lời -


Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) là tam giác vuông tại \(A\), \(AB = a\sqrt 3 \), \(BC = 2a\), đường thẳng \(AC'\) tạo với mặt phẳng \(\left( {BCC'B'} \right)\) một góc \(30^\circ \). Diện tích của mặt cầu ngoại tiếp hình lăng trụ đã cho bằng
bởi Kim Xuyen
 07/07/2022
07/07/2022
A. \(6\pi {a^2}\).
B. \(3\pi {a^2}\).
C. \(4\pi {a^2}\).
D. \(24\pi {a^2}\).
Theo dõi (0) 1 Trả lời -


Cho hình chóp \(S.\,ABC\) có \(AB = AC = 4,\,BC = 2,\,SA = 4\sqrt 3 \), . Tính thể tích khối chóp \(S.\,ABC.\)
bởi Dương Minh Tuấn
 08/07/2022
08/07/2022
A. \({V_{S.\,ABC}} = 8\).
B. \({V_{S.\,ABC}} = 6\).
C. \({V_{S.\,ABC}} = 4\).
D. \({V_{S.\,ABC}} = 12\).
Theo dõi (0) 1 Trả lời -


Cho hình chóp \(S.\,ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\) và \(\widehat {ABC} = 60^\circ \). Hình chiếu vuông góc của điểm \(S\) lên mặt phẳng \(\left( {ABCD} \right)\) trùng với trọng tâm tam giác \(ABC\). Gọi \(\varphi \) là góc giữa đường thẳng \(SB\) với mặt phẳng \(\left( {SCD} \right)\), tính \(\sin \varphi \) biết rằng \(SB = a\).
bởi Mai Đào
 07/07/2022
07/07/2022
A. \(\sin \varphi = \dfrac{1}{4}\).
B. \(\sin \varphi = \dfrac{1}{2}\).
C. \(\sin \varphi = \dfrac{{\sqrt 3 }}{2}\).
D. \(\sin \varphi = \dfrac{{\sqrt 2 }}{2}\).
Theo dõi (0) 1 Trả lời -


Cho khối nón có bán kính đáy là \(r = \sqrt 3 \) và chiều cao \(h = 4\). Tính thể tích \(V\) của khối nón đã cho.
bởi Huong Duong
 07/07/2022
07/07/2022
A. \(V = 12\pi \).
B. \(V = 4\pi \).
C. \(V = 4\).
D. \(V = 12\).
Theo dõi (0) 1 Trả lời -


Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông tại \(A\), \(SA\) vuông góc với mặt phẳng\(\left( {ABC} \right)\) và \(AB = 2,AC = 4,SA = \sqrt 5 \). Mặt cầu đi qua các đỉnh của hình chóp \(S.ABC\) có bán kính là
bởi Thuy Kim
 08/07/2022
08/07/2022
A. \(R = \dfrac{5}{2}\).
B. \(R = 5\).
C. \(R = \dfrac{{10}}{3}\).
D. \(R = \dfrac{{25}}{2}\).
Theo dõi (0) 1 Trả lời -


Cho hình chóp đều \(S.ABCD\) có cạnh \(AB = a\), góc giữa đường thẳng \(SA\) và mặt phẳng \(\left( {ABC} \right)\) bằng \(45^0\). Thể tích khối chóp \(S.\,ABCD\) là
bởi bala bala
 07/07/2022
07/07/2022
A. \(\dfrac{{{a^3}}}{3}\).
B. \(\dfrac{{{a^3}\sqrt 2 }}{6}\).
C. \(\dfrac{{{a^3}}}{6}\).
D. \(\dfrac{{{a^3}\sqrt 2 }}{3}\).
Theo dõi (0) 1 Trả lời -


Cho tứ diện \(ABCD\), gọi \({G_1},\,{G_2}\) lần lượt là trọng tâm các tam giác \(BCD\) và \(ACD\). Mệnh đề nào sau đây SAI?
bởi bach hao
 07/07/2022
07/07/2022
A. \({G_1}{G_2}//\left( {ABD} \right)\).
B. \({G_1}{G_2}//\left( {ABC} \right)\).
C. \({G_1}{G_2} = \dfrac{2}{3}AB\).
D. Ba đường thẳng \(B{G_1},\,A{G_2}\)và \(CD\) đồng quy.
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 1 trang 99 SGK Hình học 12
Bài tập 3 trang 99 SGK Hình học 12
Bài tập 4 trang 99 SGK Hình học 12
Bài tập 5 trang 99 SGK Hình học 12
Bài tập 6 trang 100 SGK Hình học 12
Bài tập 7 trang 100 SGK Hình học 12
Bài tập 8 trang 100 SGK Hình học 12
Bài tập 9 trang 100 SGK Hình học 12
Bài tập 10 trang 100 SGK Hình học 12
Bài tập 11 trang 101 SGK Hình học 12
Bài tập 12 trang 101 SGK Hình học 12
Bài tập 13 trang 101 SGK Hình học 12
Bài tập 14 trang 101 SGK Hình học 12
Bài tập 15 trang 101 SGK Hình học 12
Bài tập 16 trang 102 SGK Hình học 12
Bài tập 1 trang 122 SGK Hình học 12 NC
Bài tập 2 trang 122 SGK Hình học 12 NC
Bài tập 3 trang 122 SGK Hình học 12 NC
Bài tập 4 trang 122 SGK Hình học 12 NC
Bài tập 5 trang 122 SGK Hình học 12 NC
Bài tập 6 trang 123 SGK Hình học 12 NC
Bài tập 7 trang 123 SGK Hình học 12 NC
Bài tập 8 trang 123 SGK Hình học 12 NC
Bài tập 9 trang 123 SGK Hình học 12 NC
Bài tập 10 trang 123 SGK Hình học 12 NC
Bài tập 1 trang 127 SGK Hình học 12 NC
Bài tập 2 trang 127 SGK Hình học 12 NC
Bài tập 3 trang 127 SGK Hình học 12 NC
Bài tập 4 trang 128 SGK Hình học 12 NC
Bài tập 5 trang 128 SGK Hình học 12 NC
Bài tập 6 trang 128 SGK Hình học 12 NC
Bài tập 7 trang 128 SGK Hình học 12 NC
Bài tập 8 trang 129 SGK Hình học 12 NC
Bài tập 9 trang 129 SGK Hình học 12 NC
Bài tập 10 trang 129 SGK Hình học 12 NC
Bài tập 12 trang 129 SGK Hình học 12 NC
Bài tập 11 trang 129 SGK Hình học 12 NC
Bài tập 13 trang 129 SGK Hình học 12 NC
Bài tập 14 trang 130 SGK Hình học 12 NC
Bài tập 15 trang 130 SGK Hình học 12 NC
Bài tập 16 trang 130 SGK Hình học 12 NC
Bài tập 17 trang 130 SGK Hình học 12 NC
Bài tập 18 trang 130 SGK Hình học 12 NC
Bài tập 19 trang 131 SGK Hình học 12 NC
Bài tập 21 trang 131 SGK Hình học 12 NC
Bài tập 22 trang 131 SGK Hình học 12 NC
Bài tập 23 trang 132 SGK Hình học 12 NC
Bài tập 1 trang 168 SBT Hình học Toán 12
Bài tập 2 trang 168 SBT Hình học Toán 12
Bài tập 3 trang 169 SBT Hình học Toán 12
Bài tập 4 trang 169 SBT Hình học Toán 12
Bài tập 5 trang 169 SBT Hình học Toán 12
Bài tập 6 trang 169 SBT Hình học Toán 12
Bài tập 7 trang 169 SBT Hình học Toán 12
Bài tập 8 trang 169 SBT Hình học Toán 12
Bài tập 9 trang 170 SBT Hình học Toán 12
Bài tập 10 trang 170 SBT Hình học Toán 12
Bài tập 1 trang 170 SBT Hình học Toán 12
Bài tập 2 trang 170 SBT Hình học Toán 12
Bài tập 3 trang 170 SBT Hình học Toán 12
Bài tập 4 trang 171 SBT Hình học Toán 12
Bài tập 5 trang 171 SBT Hình học Toán 12
Bài tập 6 trang 171 SBT Hình học Toán 12
Bài tập 7 trang 171 SBT Hình học Toán 12
Bài tập 8 trang 171 SBT Hình học Toán 12
Bài tập 9 trang 171 SBT Hình học Toán 12
Bài tập 10 trang 172 SBT Hình học Toán 12
Bài tập 11 trang 172 SBT Hình học Toán 12
Bài tập 12 trang 172 SBT Hình học Toán 12
Bài tập 13 trang 172 SBT Hình học Toán 12
Bài tập 14 trang 172 SBT Hình học Toán 12
Bài tập 15 trang 172 SBT Hình học Toán 12
Bài tập 16 trang 173 SBT Hình học Toán 12
Bài tập 17 trang 173 SBT Hình học Toán 12
Bài tập 18 trang 173 SBT Hình học Toán 12
Bài tập 19 trang 173 SBT Hình học Toán 12
Bài tập 20 trang 173 SBT Hình học Toán 12
Bài tập 21 trang 173 SBT Hình học Toán 12
Bài tập 22 trang 174 SBT Hình học Toán 12





