-
Bài tập 1 trang 99 SGK Hình học 12
Cho lăng trụ lục giác đều ABCDEF.A′B′C′D′E′F′, O và O′ là tâm đường tròn ngoại tiếp hai đáy, mặt phẳng (P) đi qua trung điểm của OO′ và cắt các cạnh bên cúa lăng trụ. Chứng minh rằng (P) chia lăng trụ đã cho thành hai đa diện có thể tích bằng nhau.
-
Bài tập 2 trang 99 SGK Hình học 12
Cho khối lập phương ABCD.A'B'C'D' cạnh a. Gọi E và F lần lượt là trung điểm B'C' và C'D'. Mặt phẳng (AEF) chia khối lập phương đó thành hai khối đa diện (H) và (H') trong đó (H) là khối đa diện chứa đỉnh A'. Tính thể tích của (H).
-
Bài tập 3 trang 99 SGK Hình học 12
Cho mặt cầu (S) tâm O bán kính r. Hình nón có đường tròn đáy (C) và đỉnh I đều thuộc (S) được gọi là hình nón nội tiếp mặt cầu (S). Gọi h là chiều cao của hình nón đó.
a) Tính thể tích của hình nón theo r và h.
b) Xác định h để thể tích của hình nón là lớn nhất.
-
Bài tập 4 trang 99 SGK Hình học 12
Trong không gian Oxyz, cho hai điểm A(1;2;-1); B(7;-2;3) và đường thẳng d có phương trình \(\left\{\begin{matrix} x=-1+3t\\ y=2-2t\\ z=2+2t \end{matrix}\right.\)
a) Chứng minh rằng hai đường thẳng d và AB cùng nằm trong một mặt phẳng.
b) Tìm điểm I trên d sao cho AI + BI nhỏ nhất.
-
Bài tập 5 trang 99 SGK Hình học 12
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC). Biết rằng AC = AD = 4cm, AB = 3cm, BC = 5 cm.
a) Tính thể tích tứ diện ABCD.
b) Tính khoảng cách từ điểm A tới mặt phẳng (BCD).
-
Bài tập 6 trang 100 SGK Hình học 12
Trong không gian Oxyz cho mặt cầu (S) có phương trình \(x^2+y^2+z^2=a^2 (a>0)\)
a) Tính diện tích của mặt cầu (S) và thể tích của khối cầu tương ứng.
b) Mặt cầu (S) cắt mặt phẳng (Oxy) theo một đường tròn (C). Xác định tâm và bán kính của (C).
c) Tính diện tích xung quanh của hình trụ nhận (C) làm đáy và có chiều cao là \(a\sqrt{3}\). Tính thể tích của khối trụ tương ứng.
-
Bài tập 7 trang 100 SGK Hình học 12
Trong không gian cho hai đường thẳng d1 và d2 có phương trình
\(d_1:\left\{\begin{matrix} x=1-t\\ y=t\\ z=-t \end{matrix}\right.d_2:\left\{\begin{matrix} x=2t'\\ y=-1+t'\\ z=t' \end{matrix}\right.\)
a) Chứng minh rằng hai đường thẳng d1 và d2 chéo nhau.
b) Viết phương trình của mặt phẳng \((\alpha )\) chứa d1 và song song với d2.
-
Bài tập 8 trang 100 SGK Hình học 12
Trong không gian Oxyz cho các điểm A(1; 0; -1), B(3; 4; -2), C(4;-1;1), D(3; 0 ;3)
a) Chứng minh rằng A, B, C, D không đồng phẳng.
b) Viết phương trình mặt phẳng (ABC) và tính khoảng cách từ D đến mặt phẳng (ABC).
c) Viết phương trình mặt cầu ngoại tiếp tứ diện ABCD.
d) Tính thể tích tứ diện ABCD.
-
Bài tập 9 trang 100 SGK Hình học 12
Trong không gian Oxyz cho bốn điểm A(2; 4; -1), B(1; 4; -1), C(2; 4; 3), D(2; 2; -1).
a) Chứng mỉnh rằng các đường thẳng AB, AC, AD vuông góc với nhau từng đôi một. Tính thể tích tứ diện ABCD.
b) Viết phương tình mặt cầu (S) đi qua bốn điểm A, B, C, D.
c) Viết phương trình mặt phẳng \((\alpha )\) tiếp xúc với mặt cầu (S) và song song mặt phẳng (ABD).
-
Bài tập 10 trang 100 SGK Hình học 12
Trong không gian Oxyz cho đường thẳng \((d):\left\{\begin{matrix} x=1-2t\\ y=2+t\\ z=3-t \end{matrix}\right.\) và mặt phẳng \((\alpha ):2x+y+z=0\)
a) Tìm toạ độ giao điểm A của (d) và \((\alpha )\).
b) Viết phương trình mặt phẳng \((\beta )\) qua A và vuông góc với (d).
-
Bài tập 11 trang 101 SGK Hình học 12
Trong không gian Oxyz cho các điểm A(-1;2;0), B(-3;0;2), C(1;2;3), D(0;3;-2)
a) Viết phương trình mặt phẳng (ABC) và phương trình tham số của đường thẳng AD.
b) Viết phương trình mặt phẳng \((\alpha )\) chứa AD và song song với BC.
-
Bài tập 12 trang 101 SGK Hình học 12
Trong không gian Oxyz cho bốn điểm A(3; -2; -2), B(3; 2; 0), C(0; 2; 1) và D(-1;1;2)
a) Viết phương trình mặt phẳng (BCD). Suy ra ABCD là một tứ diện.
b) Viết phương trình mặt cầu (S) tâm A và tiếp xúc với mặt phẳng (BCD).
c) Tìm toạ độ tiếp điểm của (S) và mặt phẳng (BCD).
-
Bài tập 13 trang 101 SGK Hình học 12
Trong không gian Oxyz, cho hai đường thẳng:
\(d_1:\left\{\begin{matrix} x=-1+3t\\ y=1+2t\\ z=3-2t \end{matrix}\right.d_2:\left\{\begin{matrix} x=t'\\ y=1+t'\\ z=-3+2t' \end{matrix}\right.\)
a) Chứng minh d1 và d2 cùng thuộc một mặt phẳng.
b) Viết phương trình mặt phẳng đó.
-
Bài tập 14 trang 101 SGK Hình học 12
Trong không gian cho ba điểm A,B,C
a) Xác định điểm G sao cho \(\overrightarrow{GA}+2\overrightarrow{GB}-2\overrightarrow{GC}=\vec{0}\)
b) Tìm tập hợp các điểm M sao cho MA2 + 2MB2 - 2MC2 = k2, với k là hằng số.
-
Bài tập 15 trang 101 SGK Hình học 12
Cho hai đường thẳng chéo nhau:
\(d:\left\{\begin{matrix} x=2-t\\ y=-1+t\\ z=1-t \end{matrix}\right.; d':\left\{\begin{matrix} x=2+2t'\\ y=t'\\ z=1+t' \end{matrix}\right.\)
a) Viết phương trình các mặt phẳng \((\alpha )\) và \((\beta )\) song song với nhau và lần lượt chứa d và d'.
b) Lấy hai điểm M(2; -1; 1) và M'(2; 0; 1) lần lượt trên d và d'. Tính khoảng cách từ M đến mặt phẳng \((\beta )\) và khoảng cách từ M' đến mặt phẳng \((\alpha )\). So sánh hai khoảng cách đó.
-
Bài tập 16 trang 102 SGK Hình học 12
Trong không gian Oxyz cho mặt phẳng \((\alpha )\) có phương trình 4x + y + 2z + 1 =0 và mặt phẳng \((\beta )\) có phương trình 2x – 2y + z + 3 = 0
a) Chứng minh rằng \((\alpha )\) cắt \((\beta )\).
b) Viết phương trình tham số của đường thẳng d là giao của (α) và \((\beta )\).
c) Tìm điểm M' là ảnh của M(4; 2; 1) qua phép đối xứng qua mặt phẳng \((\alpha )\).
d) Tìm điểm N' là ảnh của N(0; 2; 4) quá phép đối xứng qua đường thẳng d.
-
Bài tập 1 trang 122 SGK Hình học 12 NC
Cho hình lăng trụ ABC.A’B’C’ với cạnh bên không vuông góc với mặt đáy. Gọi (α) là mặt phẳng vuông góc với các cạnh bên của hình lăng trụ và cắt chúng tại P, Q, R. Phép tịnh tiến theo vectơ \(\overrightarrow {AA'}\) biến tam giác PQR thành tam giác P’Q’R’.
a) Chứng minh rằng thể tích V của hình lăng trụ đã cho bằng thể tích của hình lăng trụ PQR.P’Q’R’.
b) Chứng minh rằng V = SPQR.AA′, trong đó SPQR là diện tích tam giác PQR.
-
Bài tập 2 trang 122 SGK Hình học 12 NC
Cho tứ diện ABCD có thể tích V. Hãy tính thể tích hình tứ diện có đỉnh là trọng tâm các mặt của tứ diện đã cho.
-
Bài tập 3 trang 122 SGK Hình học 12 NC
Cho hình hộp ABCD.A’B’C’D’ có thể tích V. Hãy tính thể tích của tứ diện ACB’D’.
-
Bài tập 4 trang 122 SGK Hình học 12 NC
Chứng minh rằng trung điểm các cạnh của một hình tứ diện đều là các đỉnh của một hình tám mặt đều. Hãy so sánh thể tích của tứ diện đều đã cho và thể tích của hình tám mặt đều đó.
-
Bài tập 5 trang 122 SGK Hình học 12 NC
Cho hình vuông ABCD nội tiếp đường tròn (O; R). Gọi H là hình gồm các điểm của hình tròn (O; R) nhưng không nằm trong hình vuông. Tính thể tích hình tròn xoay sinh bởi hình H khi quay quanh đường thẳng chứa một đường chéo của hình vuông.
-
Bài tập 6 trang 123 SGK Hình học 12 NC
Cho hình lục giác đều ABCDEF cạnh a.
a) Tính thể tích hình tròn xoay sinh bởi lục giác đó khi quay quanh đường thẳng AD.
b) Tính thế tích hình tròn xoay sinh bởi lục giác đó khi quay quanh đường thẳng đi qua trung điểm của các cạnh AB và DE.
-
Bài tập 7 trang 123 SGK Hình học 12 NC
Cho hình trụ có bán kính R và đường cao \(R\sqrt 2 \). Gọi AB và CD là hai đường kính thay đổi của hai đường tròn đáy mà AB vuông góc với CD.
a) Chứng minh ABCD là tứ diện đều.
b) Chứng minh rằng các đường thẳng AC, AD, BC, BD luôn tiếp xúc với một mặt trụ cố định (tức là khoảng cách giữa mỗi đường thẳng đó và trục của mặt trụ bằng bán kính mặt trụ).
-
Bài tập 8 trang 123 SGK Hình học 12 NC
Trong không gian tọa độ Oxyz cho các điểm A(1; 5; 3), B(4; 2; -5), C(5; 5; -1) và D(1; 2; 4).
a) Chứng tỏ rằng bốn điểm A, B, C, D không đồng phẳng.
b) Viết phương trình mặt cầu (S) đi qua bốn điểm A, B, C, D . Xác định tâm và bán kính của mặt cầu đó.
c) Viết phương trình mặt phẳng đi qua A, B, C và tìm khoảng cách từu điểm D tới mặt phẳng đó.
d) Viết phương trình mặt phẳng vuông góc với CD và tiếp xúc với mặt cầu (S).
e) Tìm bán kính các đường tròn giao tuyến của mặt cầu (S) và các mặt phẳng tọa độ.
-
Bài tập 9 trang 123 SGK Hình học 12 NC
Trong không gian tọa độ Oxyz cho đường thẳng Δ có phương trình \(\frac{{x - 1}}{2} = \frac{{y + 1}}{{ - 1}} = \frac{z}{3}.\)
a) Viết phương trình hình chiếu của Δ trên các mặt phẳng tọa độ.
b) Chứng minh rằng mặt phẳng \(x + 5y + z + 4 = 0\) đi qua đường thẳng Δ
c) Tính khoảng cách giữa đường thẳng Δ và các trục tọa độ.
d) Viết phương trình đường vuông góc chung của hai đường thẳng Δ và \({\rm{\Delta '}}:x = y = z.\)
e) Viết phương trình đường thẳng song song với Oz, cắt cả Δ và Δ′
-
Bài tập 10 trang 123 SGK Hình học 12 NC
Trong không gian tọa độ Oxyz, cho hai điểm A(1; -1; 2), B(2; 0; 1).
a) Tìm quỹ tích các điểm M sao cho \(M{A^2} - M{B^2} = 2.\)
b) Tìm quỹ tích các điểm N sao cho \(N{A^2} + N{B^2} = 3.\)
c) Tìm quỹ tích các điểm cách đều hai mặt phẳng (OAB) và (Oxy).
-
Bài tập 1 trang 127 SGK Hình học 12 NC
Cho H là hình chóp tứ giác đều S.ABCD. Xét các mặt phẳng (SAC), (SAB), (SBD), (ABC), (SOI), trong đó I là trung điểm của AB, O là tâm hình vuông ABCD. Trong các mặt phẳng đó, có bao nhiêu mặt phẳng là mặt phẳng đối xứng của H ?
(A) 1
(B) 2
(C) 3
(D) 4
-
Bài tập 2 trang 127 SGK Hình học 12 NC
Gọi H là lăng trụ lục giác đều ABCDEF.A’B’C’D’E’F’. Xét các mặt: mp(AA’D), mp(ACA’), mp(ABB’), mặt phẳng trung trực của DD’, mặt phẳng trung trực của AB. Trong các mặt phẳng đó, có bao nhiêu mặt phẳng là mặt phẳng đối xứng của H ?
(A) 1
(B) 2
(C) 3
(D) 4
-
Bài tập 3 trang 127 SGK Hình học 12 NC
Cho khối lăng trụ tam giác ABC.A’B’C’, M là trung điểm của cạnh AB. Trong các đẳng thức sau đây, đẳng thức nào sai ?
(A) \({V_{A'B'C'C}} = {V_{MA'B'C'}}\)
(B) \({V_{ABCC'}} = {V_{A'BCC'}}\)
(C) \({V_{MA'B'C'}} = {V_{A'ABC}}\)
(D) \({V_{MA\prime B\prime C\prime }} = \frac{1}{2}{V_{AA\prime B\prime C\prime }}\)
-
Bài tập 4 trang 128 SGK Hình học 12 NC
Cho khối lăng trụ tam giác ABC.A’B’C’ . Trong các đẳng thức sau đây, đẳng thức nào sai ?
(A) \({V_{A'BCC'}} = \frac{1}{3}{V_{ABC.A'B'C'}};\)
(B) \({V_{A.BB'C'C}} = \frac{1}{2}{V_{ABC.A'B'C'}};\)
(C) \({V_{A'.BCC'B'}} = 2{V_{AA'BC}};\)
(D) \({V_{C.ABB\prime A\prime }} = {V_{C\prime .ABB\prime A\prime }}.\)
-
Bài tập 5 trang 128 SGK Hình học 12 NC
Cho khối chóp tứ giác S.ABCD và các điểm A’, B’, C’, D’ lần lượt nằm trên các đường thẳng SA, SB, SC, SD nhưng không trùng với S.
Trong các mệnh đề sau đây, mệnh đề nào đúng ?
(A) \(\frac{{{V_{S.ABC}}}}{{{V_{S.A'B'C'}}}} = \frac{{SA}}{{SA'}}.\frac{{SB}}{{SB'}}.\frac{{SC}}{{SC'}};\)
(B) \(\frac{{{V_{S.ABCD}}}}{{{V_{S.A'B'C'D'}}}} = \frac{{SA}}{{SA'}}.\frac{{SB}}{{SB'}}.\frac{{SC}}{{SC'}}.\frac{{SD}}{{SD'}};\)
(C) \(\frac{{{V_{S.ABCD}}}}{{{V_{S.A'B'C'D'}}}} = \frac{{SA}}{{SA'}}.\frac{{SC}}{{SC'}} + \frac{{SB}}{{SB'}}.\frac{{SD}}{{SD'}};\)
(D) \(\frac{{{V_{S.ABCD}}}}{{{V_{S.A'B'C'D'}}}} = \frac{{SA}}{{SA'}} + \frac{{SB}}{{SB'}} + \frac{{SC}}{{SC'}} + \frac{{SD}}{{SD'}}.\)
-
Bài tập 6 trang 128 SGK Hình học 12 NC
Trong các mênh đề sau đây, mệnh đề nào đúng ?
(A) Hình lăng trụ nội tiếp một mặt cầu nếu đáy của nó là đa giác nội tiếp;
(B) Hình lăng trụ nội tiếp một mặt cầu nếu tất cả các mặt của nó đều là đa giác nội tiếp ;
(C) Hình lăng trụ nội tiếp một mặt cầu nếu có mặt bên vuông góc với mặt đáy ;
(D) Đa diện nội tiếp một mặt cầu nếu các mặt của nó đều là đa giác nội tiếp.
-
Bài tập 7 trang 128 SGK Hình học 12 NC
Trong các mệnh đề sau, mệnh đề nào đúng ?
(A) Đường tròn đi qua ba điểm phân biệt nằm trên mặt cầu thì nằm hoàn toàn trên mặt cầu ;
(B) Có duy nhất một mặt cầu đi qua 4 đỉnh của một hình thang cân cho trước ;
(C) Hình chóp có đáy là hình thang vuông luôn luôn nội tiếp một mặt cầu ;
(D) Cả ba mệnh đề trên đều sai.
-
Bài tập 8 trang 129 SGK Hình học 12 NC
Cho khối trụ có bán kính \(a\sqrt 3 \) và chiều cao \(2a\sqrt 3 \). Thể tích của nó là:
(A) \(4\pi {a^3}\sqrt 2 ;\)
(B) \(9{a^3}\sqrt 3 ;\)
(C) \(6\pi {a^3}\sqrt 3 ;\)
(D) \(6\pi {a^2}\sqrt 3 .\)
-
Bài tập 9 trang 129 SGK Hình học 12 NC
Đáy của một hình chóp là hình vuông có diện tích bằng 4. Các mặt bên của nó là những tam giác đều. Diện tích toàn phần của hình chóp là
(A) \(4 + 4\sqrt 3 \)
(B) 8
(C) 16
(D) \(4 + 4\sqrt 2 \)
-
Bài tập 10 trang 129 SGK Hình học 12 NC
Một hình nón có đường sinh bằng l và bằng đường kính đáy. Bán kính hình cầu ngoại tiếp hình nón là:
(A) \(\frac{1}{3}\)l
(B) \(\frac{{\sqrt 3 }}{6}\)l
(C) \(\frac{{\sqrt 2 }}{6}\)l
(D) \(\frac{3}{4}\)l.
-
Bài tập 12 trang 129 SGK Hình học 12 NC
Cho hình chữ nhật có hai đỉnh A(−2;3;0), B(2;3;0) và một cạnh nằm trên trục Ox. Khối tròn xoay sinh bởi hình chữ nhật đó khi quay quanh trục Oy có thể tích là:
(A) \(6{\pi ^2}\)
(B) 12
(C) \(12\pi \)
(D) \(\frac{{4\pi }}{3}.\)
-
Bài tập 11 trang 129 SGK Hình học 12 NC
Một hình cầu có thể tích bằng \(\frac{{4\pi }}{3}\), nội tiếp một hình lập phương. Thể tích của hình lập phương đó bằng
(A) 8
(B) \(4\pi \)
(C) 1
(D) \(2\pi \sqrt 3 \)
-
Bài tập 13 trang 129 SGK Hình học 12 NC
Cho hai vectơ \(\vec u=\left( {1;0;2} \right)\) và \(\vec v = \left( {0; - 1;1} \right)\).
Trong các vectơ sau, vectơ nào cùng phương với \(\left[ {\vec u,\vec v} \right]\)
(A) \(\vec a = \left( {1;1;1} \right)\)
(B) \(\vec b = \left( { - 2;1;1} \right)\)
(C) \(\vec c = \left( {0;1; - 1} \right)\)
(D) \(\vec d = \left( {2;2; - 1} \right).\)
-
Bài tập 14 trang 130 SGK Hình học 12 NC
Cho tam giác ABC có diện tích bằng 6 nằm trong mặt phẳng (α) có phương trình \(2x - 2y + z + 5 = 0\) Thể tích hình chóp S.ABC với S(1;1;1) bằng:
(A) \(3\sqrt 6 \)
(B) \(12\sqrt 2 \)
(C) 8
(D) 4
-
Bài tập 15 trang 130 SGK Hình học 12 NC
Mặt cầu tâm I(6; 3; -4) tiếp xúc với trục Ox có bán kính là:
(A) 5
(B) \(2\sqrt 3 \)
(C) \(4\sqrt 3 \)
(D) 4
-
Bài tập 16 trang 130 SGK Hình học 12 NC
Cho hai đường thẳng d có phương trình
\(\left\{ {\begin{array}{*{20}{c}}
{x = 1 + 2t}\\
{y = 2 - t}\\
{z = 3 + t}
\end{array}} \right.\)(A) \(\left\{ {\begin{array}{*{20}{c}}
{x = 1 + t}\\
{y = 2 - t}\\
{z = 3 + t}
\end{array}} \right.\)(B) \(\left\{ {\begin{array}{*{20}{c}}
{x = 3 + 4t}\\
{y = 1 - 2t}\\
{z = 4 + 2t}
\end{array}} \right.\)(C) \(\left\{ {\begin{array}{*{20}{c}}
{x = 2t}\\
{y = 1 - t}\\
{z = 2 + t}
\end{array}} \right.\)(D) \(\left\{ {\begin{array}{*{20}{c}}
{x = 1 + 2t}\\
{y = 2 + t}\\
{z = 3 - t}
\end{array}} \right.\) -
Bài tập 17 trang 130 SGK Hình học 12 NC
Cho hai đường thẳng
\(d:\left\{ {\begin{array}{*{20}{c}}
{x = 1 + t}\\
{y = 2 + t}\\
{z = 3 - t}
\end{array}} \right.\) và \(d':\left\{ \begin{array}{l}
x = 1 + 2t'\\
y = - 1 + 2t'\\
z = 2 - 2t'
\end{array} \right.\)Khi đó:
(A) d cắt d’
(B) d trùng d’
(C) d và d’ chéo nhau
(D) d song song với d’
-
Bài tập 18 trang 130 SGK Hình học 12 NC
Cho mặt phẳng (P) và mặt cầu (S) có phương trình
\(\begin{array}{l}
\left( P \right):3x + 4z + 12 = 0\\
\left( S \right):{x^2} + {y^2} + {\left( {z - 2} \right)^2} = 1
\end{array}\)Khi đó:
(A) mp(P) đi qua tâm cầu (S) ;
(B) mp(P) tiếp xúc với mặt cầu (S);
(C) mp(P) cắt (S) theo một đường tròn;
(D) mp(P) không cắt (S).
-
Bài tập 19 trang 131 SGK Hình học 12 NC
Tọa độ hình chiếu vuông góc của điểm M(2; 0; 1) trên đường thẳng \({\rm{\Delta }}:\frac{{x - 1}}{1} = \frac{y}{2} = \frac{{z - 2}}{1}\) là
(A) (1; 0; 2)
(B) (2; 2; 3)
(C) (0; -2 ; 1)
(D) (-1; 4; 0)
-
Bài tập 21 trang 131 SGK Hình học 12 NC
Cho hai đường thẳng
\(d:\left\{ \matrix{
x = 1 + t \hfill \cr
y = 0 \hfill \cr
z = - 5 + t \hfill \cr} \right.\) và \(d':\left\{ \begin{array}{l}x = 0\\y = 4 - 2t'\\z = 5 + 3t'\end{array} \right.\)Phương trình đường vuông góc chung của d và d’ là:
(A)
\(\left\{ \matrix{
x = 4 + 2t \hfill \cr
y = 3t \hfill \cr
z = - 2 + 2t \hfill \cr} \right.\)(B)
\(\left\{ \matrix{
x = 4 - t \hfill \cr
y = 3t \hfill \cr
z = - 2 + t; \hfill \cr} \right.\)(C) \({{x - 4} \over { - 2}} = {y \over 3} = {{z - 2} \over 2};\)
(D) \({{x - 4} \over { - 2}} = {y \over 3} = {{z + 2} \over 2}.\)
-
Bài tập 22 trang 131 SGK Hình học 12 NC
Cho mặt phẳng (P): \(mx + y + \left( {n - 2} \right)z + m + 2 = 0\)
Với mọi m, n , mặt phẳng (P) luôn đi qua điểm cố định có tọa độ là:
(A) (1; 2; 0)
(B) (2; 1; 0)
(C) (0; 1; -2)
(D) (-1; -2; 0)
-
Bài tập 23 trang 132 SGK Hình học 12 NC
Cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 2x - 4y - 4z = 0\)
Mặt phẳng tiếp xúc với (S) tại A(3; 4; 3) có phương trình:
(A) \(4x + 4y - 2z - 17 = 0\)
(B) \(2x + 2y + z - 17 = 0\)
(C) \(2x + 4y + z - 17 = 0\)
(D) \(x + y + z - 17 = 0\)
-
Bài tập 1 trang 168 SBT Hình học Toán 12
Cho lăng trụ ABC.A'B'C'
a) Tính tỉ số \(\frac{{{V_{ACA'B'}}}}{{{V_{ABC.A'B'C'}}}}\)
b) Tính VACA'B' biết rằng tam giác ABC là tam giác đều cạnh bằng a, AA' = b và AA' tạo với (ABC) một góc bằng 60o
-
Bài tập 2 trang 168 SBT Hình học Toán 12
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Gọi M, N lần lượt là trung điểm của AB và AD, H là giao điểm của MD và NC. Biết rằng SH là đường cao của hình chóp đã cho và cạnh SC tạo với đáy hình chóp đó một góc bằng 60o
a) Thể tích hình chóp S.CDNM
b) Tính khoảng cách giữa DM và SC.
-
Bài tập 3 trang 169 SBT Hình học Toán 12
Cho tứ diện ABCD có AD = BC = a, BD = CA = b, CD = AB = c.
a) Chứng minh rằng các đường vuông góc chung của các cặp cạnh đối diện đồng quy và đôi một vuông góc với nhau;
b) Tính VABCD theo a, b, c;
c) Chứng minh rằng tâm các mặt cầu nội tiếp và ngoại tiếp của tứ diện ABCD trùng nhau. Tính bán kính của các mặt cầu đó theo a, b, c.
-
Bài tập 4 trang 169 SBT Hình học Toán 12
Cho hình nón tròn xoay (H) đỉnh S, đáy là hình tròn bán kính R, chiều cao bằng h.
Gọi (H') là hình trụ tròn xoay có đáy là hình tròn bán kính r (0 < r < R) nội tiếp (H).
a) Tính tỉ số thể tích của (H') và (H);
b) Xác định r để (H') có thể tích lớn nhất.
-
Bài tập 5 trang 169 SBT Hình học Toán 12
Cho ba điểm A(1; 2; 1), B(2; -1; 1), C(0; 3; 1) và đường thẳng d: \(\frac{x}{{ - 3}} = \frac{y}{{ - 1}} = \frac{z}{2}\)
a) Viết phương trình mặt phẳng (P) đi qua A, song song với d, sao cho khoảng cách từ B đến (P) bằng khoảng cách từ C đến (P).
b) Tìm tập hợp những điểm cách đều ba điểm A, B, C.
-
Bài tập 6 trang 169 SBT Hình học Toán 12
Cho hai đường thẳng \(d:\left\{ \begin{array}{l}x = 3 + t\\y = 1 - t\\z = 2t\end{array} \right.,d':\left\{ \begin{array}{l}x = 1 + t'\\y = 2t'\\z = - 1 + t'\end{array} \right.\) và M(2; -1; 0)
a) Chứng minh rằng d và d' chéo nhau.
b) Tìm tọa độ điểm A trên d và điểm B trên d' để M, A, B thẳng hàng.
-
Bài tập 7 trang 169 SBT Hình học Toán 12
Trong không gian Oxyz, cho mặt phẳng (P): x + 2y - z + 5 = 0 và hai điểm A(-2; -1; 1), B(6; 6; 5). Trong các đường thẳng qua A và song song với (P), hãy viết phương trình đường thẳng mà khoảng cách từ B đến đường thẳng đó là nhỏ nhất.
-
Bài tập 8 trang 169 SBT Hình học Toán 12
Trong không gian Oxyz, cho mặt cầu (S): \({x^2} + {y^2} + {z^2} - 2x + 4y + 2z - 19 = 0\) và mặt phẳng (P): x - 2y + 2z - 12 = 0
a) Chứng minh rằng (P) cắt (S) theo một đường tròn.
b) Tìm tọa độ tâm và bán kính của đường tròn đó.
-
Bài tập 9 trang 170 SBT Hình học Toán 12
Trong không gian Oxyz cho hình lập phương ABCD.A’B’C’D’ với A(0;0;0), B(1;0;0), D(0;1;0), A’(0;0;1)
a) Hãy tìm tọa độ các đỉnh còn lại.
b) Chứng minh A'C ⊥ (BC'D)
c) Tìm tọa độ của chân đường vuông góc chung của B'D' và BC'.
-
Bài tập 10 trang 170 SBT Hình học Toán 12
Trong không gian Oxyz, cho S(0; 0; 2), A(0; 0; 0), B(1; 2; 0), C(0; 2; 0)
a) Viết phương trình của mặt phẳng (P) qua A và vuông góc với SB;
b) Tìm tọa độ của các điểm B' là gia của (P) với đường thẳng SB, C' là giao của (P) với đường thẳng SC;
c) Tính thể tích tứ diện SAB'C';
d) Tìm điểm đối xứng với B qua mặt phẳng (P);
e) Chứng minh các điểm A, B, C, B', C' cùng thuộc một mặt cầu. Viết phương trình của mặt cầu đó và phương trình của mặt phẳng tiếp xúc với mặt cầu đó tại C'.
-
Bài tập 1 trang 170 SBT Hình học Toán 12
Cho hình chóp ngũ giác S.ABCDE. Gọi A', B', C', D', E' lần lượt là trung điểm của SA, SB, SC, SD, SE. Khi đó \(\frac{{{V_{S.A'B'C'D'E'}}}}{{{V_{S.ABCDE}}}}\) bằng
A. 1/2 B. 1/5
C. 1/8 D. 1/32
-
Bài tập 2 trang 170 SBT Hình học Toán 12
Thể tích hình nón tròn xoay ngoại tiếp tứ diện đều cạnh a bằng:
\(\begin{array}{l}
A.\frac{{\pi {a^3}}}{9}\\
B.\frac{{\pi \sqrt 2 {a^3}}}{{18}}\\
C.\frac{{\pi \sqrt 3 {a^3}}}{{18}}\\
D.\frac{{\pi \sqrt 6 {a^3}}}{{27}}
\end{array}\) -
Bài tập 3 trang 170 SBT Hình học Toán 12
Cho hình lập phương ABCD.A'B'C'D' cạnh bằng a. Khi đó thể tích hình chóp A.A'BCD' bằng:
A. a3/2 B. a3/3
C. a3/4 D. a3/6
-
Bài tập 4 trang 171 SBT Hình học Toán 12
Cho hình lập phương ABCD.A'B'C'D'. Gọi (H) là hình nón tròn xoay nội tiếp hình lập phương đó. Khi đó: \(\frac{{{V_{\left( H \right)}}}}{{{V_{ABCD.A'B'C'D'}}}}\) bằng
A. 1/3 B. π/6
C. π/8 D. π/12
-
Bài tập 5 trang 171 SBT Hình học Toán 12
Cho hình lập phương ABCD.A'B'C'D'. Gọi (H) là hình trụ tròn xoay ngoại tiếp hình lập phương đó. Khi đó: \(\frac{{{V_{\left( H \right)}}}}{{{V_{ABCD.A'B'C'D'}}}}\) bằng
A. 3/2 B. π/2
C. π/3 D. π/(√3)
-
Bài tập 6 trang 171 SBT Hình học Toán 12
Cho hình lập phương ABCD.A'B'C'D'. Gọi (H) là hình cầu nội tiếp hình lập phương đó. Khi đó: \(\frac{{{V_{\left( H \right)}}}}{{{V_{ABCD.A'B'C'D'}}}}\) bằng
A. π/6 B. π/4
C. π/3 D. π/(√3)
-
Bài tập 7 trang 171 SBT Hình học Toán 12
Cho một mặt cầu có diện tích S, thể tích khối cầu đó là V. Bán kính R của mặt cầu là:
A. R = 4V/S B. R = S/3V
C. R = 3V/S D. R = V/3S
-
Bài tập 8 trang 171 SBT Hình học Toán 12
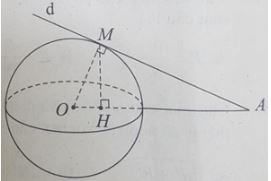
Cho mặt cầu S(O;R) và điểm A cố định với OA = d > R. Qua A kẻ đường thẳng Δ tiếp xúc với mặt cầu S(O;R) tại M. Độ dài đoạn thẳng AM là:
\(\begin{array}{l}
A.\sqrt {{d^2} + {R^2}} \\
B.\sqrt {2{R^2} - {d^2}} \\
C.\sqrt {{R^2} - 2{d^2}} \\
D.\sqrt {{d^2} - {R^2}}
\end{array}\) -
Bài tập 9 trang 171 SBT Hình học Toán 12
Gọi (S) là mặt cầu đi qua 8 đỉnh của hình hộp chữ nhật. Tâm của mặt cầu (S) là:
A. Tâm của hình hộp chữ nhật
B. Tâm của một mặt bên của hình hộp chữ nhật
C. Trung điểm của một cạnh của hình hộp chữ nhật
D. Một đỉnh bất kì của hình hộp chữ nhật
-
Bài tập 10 trang 172 SBT Hình học Toán 12
Cho mặt cầu S(O;R) và đường thẳng Δ. Biết khoảng cách từ O tới Δ bằng d. Với điều kiện nào sau đây thì đường thẳng Δ tiếp xúc với mặt cầu S(O;R)?
A. d = R B. d > R
C. d < R D. d ≠ R
-
Bài tập 11 trang 172 SBT Hình học Toán 12
Cho đường tròn (C) và điểm A nằm ngoài mặt phẳng chứa (C). Có tất cả bao nhiêu mặt cầu chứa đường tròn (C) và đi qua A?
A. 0 B. 1
C. 2 D. Vô số
-
Bài tập 12 trang 172 SBT Hình học Toán 12
Cho hai điểm A, B phân biệt. Tập hợp tâm những mặt cầu đi qua A và B là
A. Mặt phẳng trung trực của đoạn thẳng AB
B. Đường trung trực của AB
C. Mặt phẳng song song với đường thẳng AB
D. Trung điểm của đoạn AB
-
Bài tập 13 trang 172 SBT Hình học Toán 12
Từ điểm M nằm ngoài mặt cầu S(O;R) có thể kẻ được bao nhiêu tiếp tuyến với mặt cầu?
A. 0 B. 1
C. 2 D. Vô số
-
Bài tập 14 trang 172 SBT Hình học Toán 12
Một đường thẳng d thay đổi qua A và tiếp xúc với mặt cầu S(O;R) tại M. Gọi H là hình chiếu của M lên đường thẳng OA. M thuộc mặt phẳng nào trong những mặt phẳng sau đây?
A. Mặt phẳng qua H và vuông góc với OA
B. Mặt phẳng trung trực của OA
C. Mặt phẳng qua O và vuông góc với AM
D. Mặt phẳng qua A và vuông góc với OM.
-
Bài tập 15 trang 172 SBT Hình học Toán 12
Một khinh khí cầu có một mặt cầu có đường kính 11m. Nếu làm tròn kết quả đến chữ số thập phân thứ hai, thì diện tích bề mặt khinh khí cầu là:
A. 379,94 (m2) B. 697,19 (m2)
C. 190,14 (m2) D. 95,07 (m2)
-
Bài tập 16 trang 173 SBT Hình học Toán 12
Cho hình nón có thiết diện qua trục là một tam giác đều cạnh 2a và thể tích là V1 và hình cầu có đường kính bằng chiều cao hình nón, có thể tích là V2.
Tỉ số thể tích V1/V2 là:
\(\begin{array}{l}
A.\frac{{{V_1}}}{{{V_2}}} = \frac{1}{3}\\
B.\frac{{{V_1}}}{{{V_2}}} = 1\\
C.\frac{{{V_1}}}{{{V_2}}} = \frac{1}{2}\\
D.\frac{{{V_1}}}{{{V_2}}} = \frac{2}{3}
\end{array}\) -
Bài tập 17 trang 173 SBT Hình học Toán 12
Diện tích xung quanh của hình trụ có bán kính đáy a và đường cao a√3 là:
A. 2πa2√3 B. 2πa2
C. πa2 D. πa2√3
-
Bài tập 18 trang 173 SBT Hình học Toán 12
Một hình nón có đường kính đáy là 2a√3, góc ở đỉnh 120o. Thể tích của khối nón đó theo a là:
A. 2√3πa3 B. 3πa3
C. πa3 D. πa3√3
-
Bài tập 19 trang 173 SBT Hình học Toán 12
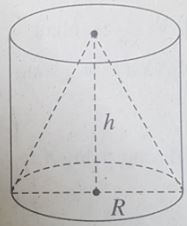
Cho một hình trụ có bán kính đáy R, chiều cao h, thể tích V1 và một hình nón có đáy trùng với đáy của một hình trụ, có đỉnh trùng với tâm đáy còn lại của hình trụ (xem hình) và thể tích V2. Hệ thức giữa V1 và V2 là:
A. V1 = 2V2 B. V1 = 3V2
C. V2 = 3V1 D. V2 = V1
-
Bài tập 20 trang 173 SBT Hình học Toán 12
Một khối trụ có chu vi đáy bằng 6π cm và thiết diện đi qua là một hình chữ nhật có độ dài đường chéo bằng 10 cm. Thể tích khối trụ là:
A. 72π (cm3) B. 24π (cm3)
C. 48π (cm3) D. 18π√(34) (cm3)
-
Bài tập 21 trang 173 SBT Hình học Toán 12
Cho A(0; 0; a), B(b; 0; 0), C(0; c; 0). Phương trình mặt phẳng (ABC) là:
\(\begin{array}{l}
A.\frac{x}{a} + \frac{y}{b} + \frac{z}{c} = 1\\
B.\frac{x}{a} + \frac{y}{c} + \frac{z}{b} = 1\\
C.\frac{x}{b} + \frac{y}{c} + \frac{z}{a} = 1\\
D.\frac{x}{c} + \frac{y}{b} + \frac{z}{a} = 1
\end{array}\) -
Bài tập 22 trang 174 SBT Hình học Toán 12
Cho ba mặt phẳng:
(P): 2x + y + z + 3 = 0
(Q): x - y - z - 1 = 0
(R): y - z + 2 = 0
Khẳng định nào sau đây là sai?
A. Không có điểm nào cùng thuộc ba mặt phẳng trên
B. (P) ⊥ (Q)
C. (P) ⊥ (R)
D. (Q) ⊥ (R)
-
Bài tập 23 trang 174 SBT Hình học Toán 12
Cho hai đường thẳng \({d_1}:\left\{ \begin{array}{l}x = t\\y = 1 - t\\z = 1 + 2t\end{array} \right.\) và \({d_2}:\left\{ \begin{array}{l}x = 1 - 2t'\\y = 2t'\\z = 3 - 4t'\end{array} \right.\)
Khẳng định nào sau đây là đúng?
A. d1 và d2 cắt nhau
B. d1 và d2 chéo nhau
C. d1 và d2 song song
D. d1 và d2 trùng nhau
-
Bài tập 24 trang 174 SBT Hình học Toán 12
Cho đường thẳng \(d:\left\{ \begin{array}{l}x = 1\\y = 1 + t\\z = - 1 + t\end{array} \right.\) và hai mặt phẳng: (P): x - y + z + 1 = 0 và (Q): 2x + y - z - 4 = 0
Khẳng định nào sau đây là đúng?
A. d // (P)
B. d // (Q)
C. d = (P) ∩ (Q)
D. d ⊥ (P).