Bài tập 1 trang 99 SGK Hình học 12
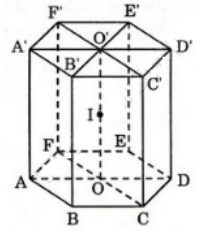
Cho lăng trụ lục giác đều ABCDEF.A′B′C′D′E′F′, O và O′ là tâm đường tròn ngoại tiếp hai đáy, mặt phẳng (P) đi qua trung điểm của OO′ và cắt các cạnh bên cúa lăng trụ. Chứng minh rằng (P) chia lăng trụ đã cho thành hai đa diện có thể tích bằng nhau.
Hướng dẫn giải chi tiết
Gọi I là trung điểm của OO′ thì I là tâm đối xứng của lăng trụ. Giả sử mặt phẳng (P) đi qua I và chia khối lăng trụ thành hai phần (H1) và (H2).
Lấy điểm M bất kì thuộc (H1) thì điểm M′ đối xứng với M cũng nằm trong hình lăng trụ, và do đó M′∈ (H2) và ngược lại, một điểm N∈(H2), lấy đối xứng qua I sẽ được N′∈(H1).
Do đó hai hình (H1) và (H2) đối xứng nhau qua tâm I.
Vì vậy thể tích (H1) bằng thể tích (H2).
Nhận xét: Trong một hình bất kì trong không gian mà có tâm đối xứng, thì mặt phẳng đi qua tâm sẽ chia hình không gian đó thành hai phần có thể tích bằng nhau.
-- Mod Toán 12 HỌC247
-


Cho hình thang cân ABCD (AB
bởi Nguyen Viet anh
 07/09/2024
07/09/2024
Cho hình thang cân ABCD (AB <CD) cạnh đáy CD và DBC = 90 Kẻ đường cao AH và BK của hình thang a) chứng minh ABKH là hình chữ nhật b) Cho, AB= 8cm BD= 10cm. Tính các cạnh và các góc của hình thang ABCD
Theo dõi (0) 0 Trả lời -


Số giao điểm của đồ thị hàm số với trục hoành
bởi Trần Mai
 18/05/2023
18/05/2023
y = x4 - x2 -22020 với trục hoành
Theo dõi (0) 0 Trả lời -


Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Hai điểm \(M,N\) thuộc các cạnh \(AB\) và \(AD\) (M, N không trùng với A, B, D). sao cho \(\dfrac{{AB}}{{AM}} + 2.\dfrac{{AD}}{{AN}} = 4\). Kí hiệu \(V,\,{V_1}\) lần lượt là thể tích của các khối chóp \(S.ABCD\) và \(S.MBCDN\). Tìm giá trị lớn nhất của tỉ số \(\dfrac{{{V_1}}}{V}\).
bởi Xuan Xuan
 08/07/2022
08/07/2022
A. \(\dfrac{2}{3}\).
B. \(\dfrac{3}{4}\)
C. \(\dfrac{1}{6}\).
D. \(\dfrac{{14}}{{17}}\).
Theo dõi (0) 2 Trả lời -


Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 4x + 2y + 6z - 1 = 0\). Tâm của mặt cầu là
bởi Lê Nhật Minh
 08/07/2022
08/07/2022
A. \(I\left( {2; - 1;3} \right)\).
B. \(I\left( { - 2;1;3} \right)\).
C. \(I\left( {2; - 1; - 3} \right)\).
D. \(I\left( {2;1; - 3} \right)\).
Theo dõi (0) 2 Trả lời -


A. \(\dfrac{{{a^3}}}{3}\).
B. \(\dfrac{{{a^3}}}{2}\).
C. \({a^3}\).
D. \(\dfrac{{{a^3}}}{6}\).
Theo dõi (0) 2 Trả lời -


Cho hình bình hành ABCD với \(A\left( { - 2;3;1} \right),B\left( {3;0; - 1} \right),\,C\left( {6;5;0} \right)\). Tọa độ đỉnh D là
bởi Hoang Viet
 08/07/2022
08/07/2022
A. \(D\left( {1;8; - 2} \right)\).
B. \(D\left( {11;2;2} \right)\).
C. \(D\left( {1;8;2} \right)\).
D. \(D\left( {11;2; - 2} \right)\).
Theo dõi (0) 1 Trả lời -


Hãy tính thể tích V của khối nón có bán kính đáy \(r = \sqrt 3 \) và chiều cao \(h = 4\).
bởi Bao Nhi
 07/07/2022
07/07/2022
A. \(V = 4\pi \).
B. \(V = 12\pi \).
C. \(V = 16\pi \sqrt 3 \).
D. \(V = 4\).
Theo dõi (0) 1 Trả lời -


Cho hai mặt phẳng \(\left( P \right)\) và \(\left( Q \right)\) song song với nhau và một điểm M không thuộc \(\left( P \right)\) và \(\left( Q \right)\). Qua M có bao nhiêu mặt phẳng vuông góc với \(\left( P \right)\) và \(\left( Q \right)\)?
bởi Lê Tấn Thanh
 07/07/2022
07/07/2022
A. 1
B. 3
C. 2
D. Vô số
Theo dõi (0) 1 Trả lời -


Khối hộp có 6 mặt đều là các hình thoi cạnh a, các góc nhọn của các mặt đều bằng \({60^0}\) có thể tích là
bởi Hương Tràm
 07/07/2022
07/07/2022
A. \(\dfrac{{{a^3}\sqrt 2 }}{3}\).
B. \(\dfrac{{{a^3}\sqrt 3 }}{6}\)
C. \(\dfrac{{{a^3}\sqrt 3 }}{3}\).
D. \(\dfrac{{{a^3}\sqrt 2 }}{2}\).
Theo dõi (0) 1 Trả lời -


Một hình trụ có chiều cao h và bán kính đáy R. Hình nón có đỉnh là tâm đáy trên của hình trụ và đáy là hình tròn đáy dưới của hình trụ. Gọi \({V_1}\) là thể tích của hình trụ, \({V_2}\) là thể tích của hình nón. Tính tỉ số \(\dfrac{{{V_1}}}{{{V_2}}}\).
bởi Bao Nhi
 07/07/2022
07/07/2022
A. 2.
B. \(2\sqrt 2 \).
C. 3.
D. \(\dfrac{1}{3}\).
Theo dõi (0) 1 Trả lời -


Tìm tọa độ điểm M trên trục Ox cách đều hai điểm \(A\left( {1;2; - 1} \right)\) và điểm \(B\left( {2;1;2} \right)\) .
bởi Anh Linh
 08/07/2022
08/07/2022
A. \(M\left( {\dfrac{1}{2};0;0} \right)\).
B. \(M\left( {\dfrac{3}{2};0;0} \right)\).
C. \(M\left( {\dfrac{2}{3};0;0} \right)\).
D. \(M\left( {\dfrac{1}{3};0;0} \right)\).
Theo dõi (0) 1 Trả lời -


Một hình trụ có thiết diện qua trục là hình vuông, diện tích xung quanh là bằng \(4\pi \). Thể tích khối trụ là
bởi Mai Hoa
 08/07/2022
08/07/2022
A \(\dfrac{2}{3}\pi \).
B \(2\pi \).
C \(4\pi \).
D \(\dfrac{4}{3}\pi \).
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 2 trang 99 SGK Hình học 12
Bài tập 3 trang 99 SGK Hình học 12
Bài tập 4 trang 99 SGK Hình học 12
Bài tập 5 trang 99 SGK Hình học 12
Bài tập 6 trang 100 SGK Hình học 12
Bài tập 7 trang 100 SGK Hình học 12
Bài tập 8 trang 100 SGK Hình học 12
Bài tập 9 trang 100 SGK Hình học 12
Bài tập 10 trang 100 SGK Hình học 12
Bài tập 11 trang 101 SGK Hình học 12
Bài tập 12 trang 101 SGK Hình học 12
Bài tập 13 trang 101 SGK Hình học 12
Bài tập 14 trang 101 SGK Hình học 12
Bài tập 15 trang 101 SGK Hình học 12
Bài tập 16 trang 102 SGK Hình học 12
Bài tập 1 trang 122 SGK Hình học 12 NC
Bài tập 2 trang 122 SGK Hình học 12 NC
Bài tập 3 trang 122 SGK Hình học 12 NC
Bài tập 4 trang 122 SGK Hình học 12 NC
Bài tập 5 trang 122 SGK Hình học 12 NC
Bài tập 6 trang 123 SGK Hình học 12 NC
Bài tập 7 trang 123 SGK Hình học 12 NC
Bài tập 8 trang 123 SGK Hình học 12 NC
Bài tập 9 trang 123 SGK Hình học 12 NC
Bài tập 10 trang 123 SGK Hình học 12 NC
Bài tập 1 trang 127 SGK Hình học 12 NC
Bài tập 2 trang 127 SGK Hình học 12 NC
Bài tập 3 trang 127 SGK Hình học 12 NC
Bài tập 4 trang 128 SGK Hình học 12 NC
Bài tập 5 trang 128 SGK Hình học 12 NC
Bài tập 6 trang 128 SGK Hình học 12 NC
Bài tập 7 trang 128 SGK Hình học 12 NC
Bài tập 8 trang 129 SGK Hình học 12 NC
Bài tập 9 trang 129 SGK Hình học 12 NC
Bài tập 10 trang 129 SGK Hình học 12 NC
Bài tập 12 trang 129 SGK Hình học 12 NC
Bài tập 11 trang 129 SGK Hình học 12 NC
Bài tập 13 trang 129 SGK Hình học 12 NC
Bài tập 14 trang 130 SGK Hình học 12 NC
Bài tập 15 trang 130 SGK Hình học 12 NC
Bài tập 16 trang 130 SGK Hình học 12 NC
Bài tập 17 trang 130 SGK Hình học 12 NC
Bài tập 18 trang 130 SGK Hình học 12 NC
Bài tập 19 trang 131 SGK Hình học 12 NC
Bài tập 21 trang 131 SGK Hình học 12 NC
Bài tập 22 trang 131 SGK Hình học 12 NC
Bài tập 23 trang 132 SGK Hình học 12 NC
Bài tập 1 trang 168 SBT Hình học Toán 12
Bài tập 2 trang 168 SBT Hình học Toán 12
Bài tập 3 trang 169 SBT Hình học Toán 12
Bài tập 4 trang 169 SBT Hình học Toán 12
Bài tập 5 trang 169 SBT Hình học Toán 12
Bài tập 6 trang 169 SBT Hình học Toán 12
Bài tập 7 trang 169 SBT Hình học Toán 12
Bài tập 8 trang 169 SBT Hình học Toán 12
Bài tập 9 trang 170 SBT Hình học Toán 12
Bài tập 10 trang 170 SBT Hình học Toán 12
Bài tập 1 trang 170 SBT Hình học Toán 12
Bài tập 2 trang 170 SBT Hình học Toán 12
Bài tập 3 trang 170 SBT Hình học Toán 12
Bài tập 4 trang 171 SBT Hình học Toán 12
Bài tập 5 trang 171 SBT Hình học Toán 12
Bài tập 6 trang 171 SBT Hình học Toán 12
Bài tập 7 trang 171 SBT Hình học Toán 12
Bài tập 8 trang 171 SBT Hình học Toán 12
Bài tập 9 trang 171 SBT Hình học Toán 12
Bài tập 10 trang 172 SBT Hình học Toán 12
Bài tập 11 trang 172 SBT Hình học Toán 12
Bài tập 12 trang 172 SBT Hình học Toán 12
Bài tập 13 trang 172 SBT Hình học Toán 12
Bài tập 14 trang 172 SBT Hình học Toán 12
Bài tập 15 trang 172 SBT Hình học Toán 12
Bài tập 16 trang 173 SBT Hình học Toán 12
Bài tập 17 trang 173 SBT Hình học Toán 12
Bài tập 18 trang 173 SBT Hình học Toán 12
Bài tập 19 trang 173 SBT Hình học Toán 12
Bài tập 20 trang 173 SBT Hình học Toán 12
Bài tập 21 trang 173 SBT Hình học Toán 12
Bài tập 22 trang 174 SBT Hình học Toán 12