Bài tập 13 trang 172 SBT Hình học Toán 12
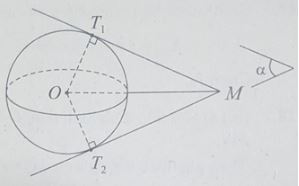
Từ điểm M nằm ngoài mặt cầu S(O;R) có thể kẻ được bao nhiêu tiếp tuyến với mặt cầu?
A. 0 B. 1
C. 2 D. Vô số
Hướng dẫn giải chi tiết Bài tập 13 trang 172
Gọi (α) là mặt phẳng chứa đường thẳng MO
Ta có: (α) cắt mặt cầu S(O;R) theo giao tuyến là đường tròn (C) có tâm O, bán kính R.
Trong mặt phẳng (α), từ điểm M nằm ngoài (C) ta luôn kẻ được hai tiếp tuyến MT1, MT2 với đường tròn (C). Đây cũng là hai tiếp tuyến với mặt cầu S(O;R).
Nhận xét: Do có vô số mặt phẳng (α) chứa đường thẳng MO. Những mặt phẳng này cắt mặt cầu S(O;R) theo các giao tuyến là đường tròn khác nhau nên cũng có vô số tiếp tuyến với mặt cầu được kẻ từ điểm M nằm ngoài mặt cầu.
Chọn D.
-- Mod Toán 12 HỌC247
-


Cho biết hình lập phương có bao nhiêu mặt phẳng đối xứng?
bởi Vu Thy
 06/05/2021
06/05/2021
A. 6
B. 7
C. 8
D. 9
Theo dõi (0) 1 Trả lời -


Hãy tính diện tích của mặt cầu ngoại tiếp hình lăng trụ tam giác đều có tất cả các cạnh bằng a.
bởi Lê Trung Phuong
 06/05/2021
06/05/2021
A. \({\rm{S}} = \frac{{7\pi {a^2}}}{3}\)
B. \({\rm{S}} = \frac{{\pi {a^3}}}{8}\)
C. \({\rm{S}} = \pi {a^2}\)
D. \({\rm{S}} = \frac{{7\pi {a^2}}}{9}\)
Theo dõi (0) 1 Trả lời -


Tứ diện ABCD, trên các cạnh BC, BD, AC lần lượt lấy các điểm M, N, P sao cho \(BC = 3BM,BD = \frac{3}{2}BN,\) \(AC = 2AP\). Mặt phẳng \(\left( {MNP} \right)\) chia khối tứ diện ABCD thành hai khối đa diện có thể tích là \({V_1},{V_2}\), trong đó khối đa diện chứa cạnh CD có thể tích là \({V_2}\). Hãy tính tỉ số \(\frac{{{V_1}}}{{{V_2}}}\).
bởi thủy tiên
 07/05/2021
07/05/2021
A. \(\frac{{{V_1}}}{{{V_2}}} = \frac{{26}}{{19}}\)
B. \(\frac{{{V_1}}}{{{V_2}}} = \frac{{26}}{{13}}\)
C. \(\frac{{{V_1}}}{{{V_2}}} = \frac{{15}}{{19}}\)
D. \(\frac{{{V_1}}}{{{V_2}}} = \frac{3}{{19}}\)
Theo dõi (0) 1 Trả lời -


Không gian \({\rm{Oxyz}}\), cho điểm \(A\left( {2; - 1; - 3} \right)\) và mặt phẳng \(\left( P \right):3{\rm{x}} - 2y + 4{\rm{z}} - 5 = 0\). Mặt phẳng \(\left( Q \right)\) đi qua A và song song với mặt phẳng \(\left( P \right)\) có phương trình là:
bởi An Vũ
 07/05/2021
07/05/2021
A. \(\left( Q \right):3{\rm{x}} - 2y + 4z - 4 = 0\)
B. \(\left( Q \right):3{\rm{x}} - 2y + 4z + 4 = 0\)
C. \(\left( Q \right):3{\rm{x}} - 2y + 4z + 5 = 0\)
D. \(\left( Q \right):3{\rm{x + }}2y + 4z + 8 = 0\)
Theo dõi (0) 1 Trả lời -


Không gian Oxyz, cho \(A\left( {0;0;2} \right),{\mkern 1mu} {\mkern 1mu} B\left( {1;1;0} \right)\) và mặt cầu \(\left( S \right):{\mkern 1mu} {\mkern 1mu} {x^2} + {y^2} + {\left( {z - 1} \right)^2} = \dfrac{1}{4}\). Xét điểm \(M\) thay đổi thuộc \(\left( S \right)\). Giá trị nhỏ nhất của biểu thức \(M{A^2} + 2M{B^2}\) bằng bao nhiêu?
bởi na na
 07/05/2021
07/05/2021
A. \(\dfrac{1}{2}\)
B. \(\dfrac{3}{4}\)
C. \(\dfrac{{21}}{4}\)
D. \(\dfrac{{19}}{4}\)
Theo dõi (0) 1 Trả lời -


Không gian Oxyz phương trình đường thẳng đi qua hai điểm \(A\left( { - 3;1;2} \right)\), \(B\left( {1; - 1;0} \right)\) có dạng:
bởi Lê Bảo An
 07/05/2021
07/05/2021
A. \(\dfrac{{x + 3}}{2} = \dfrac{{y - 1}}{1} = \dfrac{{z - 2}}{{ - 1}}\)
B. \(\dfrac{{x - 1}}{{ - 2}} = \dfrac{{y + 1}}{{ - 1}} = \dfrac{z}{1}\)
C. \(\dfrac{{x - 1}}{2} = \dfrac{{y + 1}}{{ - 1}} = \dfrac{z}{{ - 1}}\)
D. \(\dfrac{{x + 3}}{2} = \dfrac{{y - 1}}{{ - 1}} = \dfrac{{z - 2}}{{ - 1}}\)
Theo dõi (0) 1 Trả lời -


Số tự nhiên \(n\) thỏa mãn \(C_n^0 + C_n^1 + C_n^2 = 11.\) Cho biết số hạng chứa \({x^7}\) trong khai triển của \({\left( {{x^3} - \dfrac{1}{{{x^2}}}} \right)^n}\) bằng:
bởi Dương Minh Tuấn
 06/05/2021
06/05/2021
A. \( - 4\)
B. (9{x^2}
C. \( - 4{x^7}\)
D. \( - 12{x^7}\)
Theo dõi (0) 1 Trả lời -


Một khối lập phương biết rằng khi tăng độ dài cạnh của khối lập phương thêm \(2{\mkern 1mu} {\mkern 1mu} cm\) thì thể tích của nó tăng thêm \(98{\mkern 1mu} {\mkern 1mu} c{m^3}\). Cạnh của khối lập phương đã cho bằng:
bởi Nguyễn Trọng Nhân
 07/05/2021
07/05/2021
A. \(3{\mkern 1mu} {\mkern 1mu} cm\)
B. \(4{\mkern 1mu} {\mkern 1mu} cm\)
C. \(6{\mkern 1mu} {\mkern 1mu} cm\)
D. \(5{\mkern 1mu} {\mkern 1mu} cm\)
Theo dõi (0) 1 Trả lời -


Cho biết có bao nhiêu giá trị nguyên của \(m\) để hàm số \(y = \dfrac{{mx + 4}}{{x + m}}\) nghịch biến trên khoảng \(\left( { - 1;{\mkern 1mu} {\mkern 1mu} 1} \right)?\)
bởi Anh Nguyễn
 07/05/2021
07/05/2021
A. \(4\)
B. \(2\)
C. \(5\)
D. \(0\)
Theo dõi (0) 1 Trả lời -


Hai đường thẳng song song \({d_1},{\mkern 1mu} {d_2}\). Trên \({d_1}\) có 6 điểm phân biệt được tô màu đỏ. Trên \({d_2}\) có 4 điểm phân biệt được tô màu xanh. Xét tất cả các tam giác được tạo thành khi nối các điểm đó với nhau. Chọn ngẫu nhiên 1 tam giác, khi đó xác suất để thu được tam giác có 2 đỉnh màu đỏ là:
bởi het roi
 07/05/2021
07/05/2021
A. \(\dfrac{5}{9}.\)
B. \(\dfrac{5}{{32}}.\)
C. \(\dfrac{5}{8}.\)
D. \(\dfrac{5}{7}.\)
Theo dõi (0) 1 Trả lời -


Trong không gian Oxyz, mặt phẳng \(\left( P \right)\) chứa hai đường thẳng \({d_1}:{\mkern 1mu} {\mkern 1mu} \dfrac{{x - 2}}{2} = \dfrac{{y + 3}}{{ - 1}} = \dfrac{{z - 5}}{{ - 3}}\) và \({d_2}:{\mkern 1mu} {\mkern 1mu} \dfrac{{x + 1}}{{ - 2}} = \dfrac{{y + 3}}{1} = \dfrac{{z - 2}}{3}.\) Cho biết phương trình mặt phẳng \(\left( P \right)\) là:
bởi Nguyễn Thủy
 07/05/2021
07/05/2021
A. \(x - 5y - z + 18 = 0\)
B. \(x - 5y + z - 22 = 0\)
C. \(x + 5y - z + 18 = 0\)
D. \(x + 3y - z + 12 = 0\)
Theo dõi (0) 1 Trả lời -


Trong không gian Oxyz, cho đường thẳng \(d:\dfrac{{x - 3}}{4} = \dfrac{{y + 1}}{{ - 2}} = \dfrac{{z + 2}}{3}\). Cho biết Vectơ nào dưới đây là một vectơ chỉ phương của d?
bởi Nguyễn Thanh Hà
 07/05/2021
07/05/2021
A. \(\overrightarrow {{u_3}} {\rm{\;}} = \left( {3; - 1; - 2} \right)\).
B. \(\overrightarrow {{u_4}} {\rm{\;}} = \left( {4;2;3} \right)\).
C. \(\overrightarrow {{u_2}} {\rm{\;}} = \left( {4; - 2;3} \right)\).
D. \(\overrightarrow {{u_1}} {\rm{\;}} = \left( {3;1;2} \right)\).
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 11 trang 172 SBT Hình học Toán 12
Bài tập 12 trang 172 SBT Hình học Toán 12
Bài tập 14 trang 172 SBT Hình học Toán 12
Bài tập 15 trang 172 SBT Hình học Toán 12
Bài tập 16 trang 173 SBT Hình học Toán 12
Bài tập 17 trang 173 SBT Hình học Toán 12
Bài tập 18 trang 173 SBT Hình học Toán 12
Bài tập 19 trang 173 SBT Hình học Toán 12
Bài tập 20 trang 173 SBT Hình học Toán 12
Bài tập 21 trang 173 SBT Hình học Toán 12
Bài tập 22 trang 174 SBT Hình học Toán 12