Bài tập 14 trang 172 SBT Hình học Toán 12
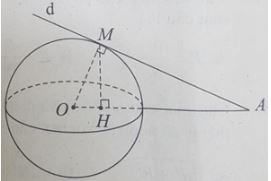
Một đường thẳng d thay đổi qua A và tiếp xúc với mặt cầu S(O;R) tại M. Gọi H là hình chiếu của M lên đường thẳng OA. M thuộc mặt phẳng nào trong những mặt phẳng sau đây?
A. Mặt phẳng qua H và vuông góc với OA
B. Mặt phẳng trung trực của OA
C. Mặt phẳng qua O và vuông góc với AM
D. Mặt phẳng qua A và vuông góc với OM.
Hướng dẫn giải chi tiết Bài tập 14 trang 172
Trong mặt phẳng (d,O), tam giác OMA vuông tại M có MH là đường cao nên:
\(O{M^2} = OH.OA\) \( \Rightarrow OH = \frac{{{R^2}}}{{OA}} = const\)
⇒ H cố định
Vậy M thuộc mặt phẳng vuông góc với OA tại H.
Chọn A.
-- Mod Toán 12 HỌC247
-


Trong không gian Oxyz, cho hai điểm \(A\left( {1;1;2} \right),B\left( {2;0;1} \right)\). Mặt phẳng đi qua A và vuông góc với đường thẳng AB có phương trình là phương án nào dưới đây?
bởi Bình Nguyen
 07/05/2021
07/05/2021
A. \(x + y - z = 0\).
B. \(x - y - z - 2 = 0\).
C. \(x + y + z - 4 = 0\).
D. \(x - y - z + 2 = 0\).
Theo dõi (0) 1 Trả lời -


Không gian Oxyz, cho mặt phẳng \(\left( P \right):2x - y + 2z + 1 = 0\) và hai điểm \(A\left( {1;0; - 2} \right),\)\(B\left( { - 1; - 1;3} \right)\). Mặt phẳng \(\left( Q \right)\) đi qua hai điểm A, B và vuông góc với mặt phẳng \(\left( P \right)\) có phương trình là đáp án nào?
bởi Duy Quang
 06/05/2021
06/05/2021
A. \(3x + 14y + 4z - 5 = 0.\)
B. \(2x - y + 2z - 2 = 0.\)
C. \(2x - y + 2z + 2 = 0.\)
D. \(3x + 14y + 4z + 5 = 0.\)
Theo dõi (0) 1 Trả lời -


Ở làng gốm truyền thống Bát Tràng dự kiến làm một bức tranh gồm hình vuông cạnh \(4{\mkern 1mu} {\mkern 1mu} \left( m \right)\), thiết kế có 4 đường parabol chung đỉnh tại tâm của hình vuông, tạo nên bốn cánh hoa (tham khảo hình vẽ). Phần diện tích cánh hoa (phần tô đậm) sẽ được tráng một lớp men đặc biệt. Chi phí tráng lớp men đó có đơn giá là 24 triệu đồng/\({m^2}\). Hãy tính số tiền phải trả để tráng men cho 4 cánh hoa.
bởi Nguyễn Tiểu Ly
 07/05/2021
07/05/2021
A. 132 triệu
B. 96 triệu
C. 32 triệu
D. 128 triệu
Theo dõi (0) 1 Trả lời -


Khối lăng trụ tứ giác đều ABCD.A’B’C’D’ có cạnh đáy bằng a và mặt phăng (DBC’) hợp với mặt đáy (ABCD) một góc \({60^0}\). Tính theo a thể tích của khối lăng trụ ABCD.A’B’C’D’.
bởi Lan Ha
 07/05/2021
07/05/2021
A. \(\dfrac{{\sqrt 6 {a^3}}}{2}\)
B. \(\sqrt 6 {a^3}\)
C. \(\dfrac{{\sqrt 6 {a^3}}}{6}\)
D. \(\dfrac{{\sqrt 6 {a^3}}}{3}\)
Theo dõi (0) 1 Trả lời -


Thể tích của khối tròn xoay khi cho hình phẳng giới hạn bởi đường thẳng \(3x - 2\) và đồ thị hàm số \(y = {x^2}\) quanh quanh trục Ox.
bởi Trinh Hung
 07/05/2021
07/05/2021
A. \(\dfrac{1}{6}\)
B. \(\dfrac{\pi }{6}\)
C. \(\dfrac{4}{5}\)
D. \(\dfrac{{4\pi }}{5}\)
Theo dõi (0) 1 Trả lời -


Họ nguyên hàm của hàm số \(f\left( x \right) = {x^2} + 2x\) là đáp án nào dưới đây?
bởi Thúy Vân
 06/05/2021
06/05/2021
A. \(\dfrac{1}{3}{x^3} + 2x + C\)
B. \(2x + 2 + C\)
C. \({x^3} + {x^2} + C\)
D. \(\dfrac{1}{3}{x^3} + {x^2} + C\)
Theo dõi (0) 1 Trả lời -


Diện tích hình phẳng giới hạn bơi đường thẳng \(y = x + 3\) và parabol \(y = 2{x^2} - x - 1\) bằng bao nhiêu?
bởi Nguyen Ngoc
 07/05/2021
07/05/2021
A. \(9\)
B. \(\dfrac{{13}}{6}\)
C. \(\dfrac{{13}}{3}\)
D. \(\dfrac{9}{2}\)
Theo dõi (0) 1 Trả lời -


Hình chóp \(S.ABCD\) có đáy là hình chữ nhật, tam giác \(SAB\) đều và nằm trong mặt phẳng vuông góc với đáy, \(AB = a;\,\,AD = a\sqrt 3 \). Thể tích khối chóp S.ABCD bằng bao nhiêu?
bởi Bảo Anh
 07/05/2021
07/05/2021
A. \(\dfrac{{3{a^2}}}{2}.\)
B. \({a^3}\)
C. \(\dfrac{{{a^3}}}{6}.\)
D. \(\dfrac{{{a^3}}}{2}\)
Theo dõi (0) 1 Trả lời -


Hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đồ thị như hình vẽ bên. Số nghiệm của phương trình \(f\left( {1 - f\left( x \right)} \right) = 2\) là đáp án nào?
bởi Tuấn Tú
 07/05/2021
07/05/2021
.jpg)
A. \(2\)
B. \(3\)
C. \(5\)
D. \(4\)
Theo dõi (0) 1 Trả lời -


Hình chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh bằng \(\sqrt 2 a\). Tam giác SAD cân tại \(S\) và mặt bên \(\left( {SAD} \right)\) vuông góc với mặt phẳng đáy. Biết thể tích khối chóp S.ABCD bằng \(\dfrac{4}{3}{a^3}\). Tính khoảng cách h từ \(B\) đến mặt phẳng \(\left( {SCD} \right)\).
bởi Mai Vi
 07/05/2021
07/05/2021
A. \(h = \dfrac{2}{3}a\)
B. \(h = \dfrac{4}{3}a\)
C. \(h = \dfrac{8}{3}a\)
D. \(h = \dfrac{3}{4}a\)
Theo dõi (0) 1 Trả lời -


Hình chóp S.ABCD có đáy là hình thoi, tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng \(\left( {ABCD} \right)\). Biết \(AC = 2a,{\mkern 1mu} {\mkern 1mu} BD = 4a\). Hãy tính theo \(a\) khoảng cách giữa hai đường thẳng AD và SC.
bởi Long lanh
 07/05/2021
07/05/2021
A. \(\dfrac{{a\sqrt {15} }}{2}\).
B. \(\dfrac{{2a\sqrt 5 }}{5}\).
C. \(\dfrac{{2{a^3}\sqrt {15} }}{3}\).
D. \(\dfrac{{4a\sqrt {1365} }}{{91}}\).
Theo dõi (0) 1 Trả lời -


Có tập nghiệm của bất phương trình \({\log _{\dfrac{1}{3}}}\dfrac{{1 - 2x}}{x} > 0\) có dạng \(\left( {a;b} \right)\). Hãy tính \(T = 3a - 2b.\)
bởi Thanh Nguyên
 06/05/2021
06/05/2021
A. \(T = 0.\)
B. \(T = {\rm{\;}} - 1.\)
C. \(T = 1.\)
D. \(T = \dfrac{{ - 2}}{3}.\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 12 trang 172 SBT Hình học Toán 12
Bài tập 13 trang 172 SBT Hình học Toán 12
Bài tập 15 trang 172 SBT Hình học Toán 12
Bài tập 16 trang 173 SBT Hình học Toán 12
Bài tập 17 trang 173 SBT Hình học Toán 12
Bài tập 18 trang 173 SBT Hình học Toán 12
Bài tập 19 trang 173 SBT Hình học Toán 12
Bài tập 20 trang 173 SBT Hình học Toán 12
Bài tập 21 trang 173 SBT Hình học Toán 12
Bài tập 22 trang 174 SBT Hình học Toán 12