Giải bài 72 tr 147 sách BT Toán lớp 7 Tập 1
Cho tam giác \(ABC\) cân tại \(A.\) Trên tia đối của tia \(BC\) lấy điểm \(D\), trên tia đối của tia \(CB\) lấy điểm \(E\) sao cho \(BD = CE.\) Chứng minh rằng \(∆ADE\) là tam giác cân.
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Tam giác có hai cạnh bằng nhau là tam giác cân.
- Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
Lời giải chi tiết
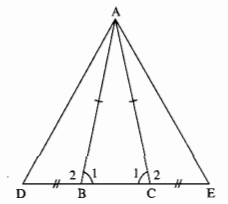
\( ∆ABC\) cân tại \(A\) nên \(\widehat {{B_1}} = \widehat {{C_1}}\) (tính chất tam giác cân)
Lại có: \(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \) (hai góc kề bù)
\(\widehat {{C_1}} + \widehat {{C_2}} = 180^\circ \) (hai góc kề bù)
\( \Rightarrow \widehat {{B_2}} = \widehat {{C_2}}\)
Xét \(∆ABD\) và \(∆ACE\) có:
\(AB = AC\) (vì \( ∆ABC\) cân tại \(A\))
\(\widehat {{B_2}} = \widehat {{C_2}}\) (chứng minh trên)
\(BD = CE\) (gt)
\( \Rightarrow ∆ABD = ∆ACE\) (c.g.c)
\( \Rightarrow AD = AE\) (hai cạnh tương ứng)
\(∆ADE\) có \(AD=AE\) nên \(∆ADE\) cân tại \(A\) (theo định nghĩa tam giác cân).
-- Mod Toán 7 HỌC247
-


Chứng minh HJ//EF biết tam giác DEF có DE=DF=5cm, EF=6cm, I là trung điểm EF
bởi Tuấn Huy
 08/04/2019
08/04/2019
Cho tam giác DEF có DE = DF = 5 cm, EF = 6 cm. Gọi I là trung điểm của EF
a) Chứng minh tam giác DEI = tam giác DFI
b) Tính độ dài đoạn DI
c) Kẻ IH vuông góc với DE (H thuộc DE). Kẻ IJ vuông góc với DF (J thuộc DF). Chứng minh tam giác IHJ là tam giác cân
d) Chứng minh HJ // EF
Theo dõi (0) 1 Trả lời -


cho tam giá ABC cân tại A.tia đối của tia BC lấy điểm D trên tia đối của tia CB lấy điểm E sao cho BD =CE .Kẻ BH vuông góc với AD tại H CK vuông góc với AE tại K.Hai đường thẳng HB và KC cắt nhau tại I.Chứng minh:
a)tam giác ADE cân
b)tam giác BIC cân
c)IA là tia phân giác của góc BIC
Theo dõi (0) 1 Trả lời -


Bài 1 cho tam giác ABC cân tại A biết góc C bằng70 độ
a) tính góc B và góc C
b) so sánh các canh của tam giác ABC
Theo dõi (0) 1 Trả lời -


Bài 1: Cho △ABC có AB=AC. Trên cạnh AB lấy điểm E, trên cạnh AC lấy điểm D sao cho AE=AD, gọi I là giao điểm của BD và CE, F là trung điểm của BC. Chứng minh:
a, BD=CE
b, △CEB=△BDC
c, △BIE=△CID
d, Ba điểm A, I, F thẳng hàng
Bài 2: Cho góc nhọn xOy, A∈ Ox, B∈ Oy, OA=OB. Qua điểm A kẻ đường thẳng vuông góc với Ox cắt Oy tại M. Qua B kẻ 1 đường thẳng vuông góc với Oy cắt Ox tại N. Gọi H là giao điểm của AM và BN. I là trung điểm của MN. Chứng minh rằng:
a, ON=OM và AN=BM
b, Tia OH là tia phân giác của góc xOy.
c, Ba điểm O, H, I thẳng hàng
AI GIÚP EM GIẢI CHI TIẾT 2 BÀI TRÊN RA, ĐẶC BIỆT LÀ PHẦN c MỖI BÀI RA VỚI!!!ĐỀ THI NGÀY MAI CỦA TỤI EM CÓ DẠNG NHƯ TRÊN. EM ĐANG RẤT CẦN. HỨA LÀ EM SẼ TICK CHO NHÉ!!
Theo dõi (0) 1 Trả lời -


Chứng minh ND là phân giác góc MNC biết tam giác ABC cân tại A có phân giác AD
bởi Phạm Phú Lộc Nữ
 09/04/2019
09/04/2019
Cho tam giác ABC cân tại A , đường phân giác AD . Từ D vẽ DM // AC ( M thuộc AB ) .
a) CMR : M là trung điểm của AB .
b) Gọi G là giao điểm của AD và CM . CMR : GD = 1/2 GA
c) TRên tia AC lấy điểm N sao cho \(\widehat{DMB}=\widehat{DMN}\)
CMR : ND là phân giác \(\widehat{MNC}\)
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ADE cân tại A biết tam giác ABC cân tại A có phân giác góc B, C
bởi minh dương
 08/04/2019
08/04/2019
Cho \(\Delta ABC\) cân tại A. Tia phân giác \(\widehat{B},\widehat{C}\) lần lượt cắt AC, AB ở D và E. CMR:
a) \(\Delta ADE\) cân tại A.
b) DE//BC.
c) BE=DE=CD.
Theo dõi (0) 1 Trả lời -


cho đoạn thẳng AB và điểm M nằm giữa A và B (MA<MB). Vẽ tia Mx vuông góc vs AB, trên đó lấy 2 điểm C và D, sao cho MA=MC, MD=MB. Tia AC cắt BD ở E. Chứng minh rằng:
a, AE vuông góc vs BD
b, Chứng minh D là trực tâm của tam giác ABC
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC , M là trung điểm của BC và AM là tia phân giác của góc A . Chứng minh tam giác ABC cân .
Theo dõi (0) 1 Trả lời -


Tính các góc nhọn tam giác vuông có đường cao ứng với cạnh huyền bằng 2cm
bởi Lê Nhật Minh
 08/04/2019
08/04/2019
trong một tam giác vuông đường cao ứng với cạnh huyền bằng 2 cm, một cạnh góc vuông bằng 4cm. Tính các góc nhọn của tam giác vuông đó
Ai giỏi toán giải giùm mk bài này nhá!!!Cần gấp lắm lun í
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh AE//HC biết tam giác ABC vuông tại A có BD là phân giác của góc B
bởi Dương Quá
 08/04/2019
08/04/2019
Tam giác ABC vuông tại a, BD là tia phân giác của góc B, trên tia BC lấy điểm E sao cho BA=BE. Gọi H là trung điểm của AB và DE.
a. chứng minh DE vuông góc với BỀ b.chứng minh BD là đường trung trực của AE c.Chứng minh AE//HC
Theo dõi (0) 1 Trả lời -


cho tam giác abc có ab=ac trên tia đối tia bc lấy d trên tia đối tia ba lấy e sao cho ed=eb
a)CMR ed song song ac
gọi h là trung điểm của db i là trung điểm bc CMR eh song song ai
Theo dõi (0) 1 Trả lời -


Cho \(\Delta ABC\) . Tia phân giác của góc B cắt AC ở D, trên tia đối của tia BA lấy E sao cho BE = BC. Chứng minh rằng: BD // EC
Theo dõi (0) 1 Trả lời -


Tính chu vi tam giác cân ABC biết AB=7cm, AC=13cm
bởi Hoa Lan
 09/04/2019
09/04/2019
Bài 1:Chu vi của 1 tam giác cân là 62cm.1 cạnh dài 25cm.Tính các cạnh của tam giác cân đó
Bài 2: Tính chu vi của 1 tam giác cân biết:
a) AB=7cm;AC=13cm
b)AB=5cm;AC=12cm
Theo dõi (0) 1 Trả lời -


Chứng minh HK song song BC biết tam giác ABC cân tại A có BH, CK vuông góc với AD, AE
bởi Thanh Nguyên
 08/04/2019
08/04/2019
Cho \(\Delta ABC\) cân tại A. Trên tia đối của tia BC và CB lấy theo thứ tự lần lượt là D và E sao cho BD=CE
a) CM: \(\Delta ADE\) cân
b) GỌi M là trung điểm của BC. CMR: AM là tia phân giác của \(\widehat{DAE}\) và \(AM\perp DE\)
c) Từ B và C kẻ BH và CK theo thứ tự vuông góc với AD và AE. CMR: BH=CK
d) CM: HK//BC
e) Cho HB cắt CK ở N. CM: A,M,N thẳng hàng.
Theo dõi (0) 2 Trả lời -


cho ΔABC nhọn có đường cao AH.Kẻ HM⊥AB ở M rồi kéo dài lấy MI=MH.Kẻ HN⊥AC ở N rồi kéo dài lấy NK=NH. Chứng minh:AI=AK giúp mik nke!!!!
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABM đều biết tam giác ABC có đường cao AH và trung tuyến AM
bởi Ban Mai
 08/04/2019
08/04/2019
Chương II: Tam giác
Một số bài nâng cao
Bài 1. Tam giác ABC có đường cao AH và trung tuyến AM chia góc A thành ba góc bằng nhau. Chứng minh rằng ∆ABC là tam giác vuông và ∆ABM là tam giác đều.
Bài 2. Cho tam giác ABC (AB < AC). Từ trung điểm M của BC kẻ đường vuông góc với tia phân giác của góc A cắt tia này tại H, cắt AB, AC lần lượt tại D và E. Chứng minh rằng: BD = CE.
Bài 3. Cho tam giác ABC cân tại A, có góc A = 20o. Trên cạnh AB lấy điểm D sao cho AD = BC. Chứng minh rằng góc DCA = 1/2 góc A.
Gợi ý:
- Vẽ ∆BEC đều (Điểm E ở cùng một nửa mặt phẳng bờ BC với điểm A).
- Chứng minh góc DCA = góc EAC.
Bài 4. Cho ∆ABC vuông tại A, có góc C = 15o. Trên tia BA lấy điểm O sao cho BO = 2AC. Chứng minh rằng ∆OBC cân.
Gợi ý:
- Vẽ ∆DBC đều (D và A thuộc cùng một nửa mặt phẳng bờ BC)
- Chứng minh góc BDC = 2 góc BOC
⇒ góc BOC = 30o ⇒ góc OCB = 75o.
Bài 5. Cho ∆ABC cân tại A có góc A = 108o. Gọi O là một điểm nằm trên tia phân giác của góc C sao cho góc CBO = 12o. Vẽ tam giác đều BOM (M và A cùng thuộc một nửa mặt phẳng bờ BO). Chứng minh rằng:
a/ Ba điểm C, A, M thẳng hàng
b/ Tam giác AOB cân
Theo dõi (0) 1 Trả lời -


1) Cho \(\Delta ABC\)vuông góc tại A . Đường phân giác CH của góc c cắt AB tại H . Vẽ HK vuông góc vs BC tại K ( K \(\in\)BC)
a) C/m \(\Delta AHC=\Delta KHC\)
b) C/m \(\Delta AHC\)cân
2) Cho \(\Delta DEP\)có DE = 10cm ; DF = 24cm;EF = 26cm . C/m \(\Delta DEF\)là tam giác vuông
*3) Cho \(\Delta ABC\)có góc A = 900 ; AB < AC . Đường phân giác BE ( E \(\in\)AC ) lấy điểm H thuộc cạnh BC sao cho BH = BA .
a) C/m EH \(\perp\)BC
b) C/m BE là đường trung trực của AH
c) Đường thẳng EM cắt đường thẳng AB ở K . C/m EK = EC
d) C/m AH // KC
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác MNF=tam giác MPE biết tam giác MNP cân tại M
bởi Phạm Hoàng Thị Trà Giang
 25/02/2019
25/02/2019
Bài 2: Cho tam giác ABC có AB=AC=5cm, BC=8cm. Kẻ AH vuông góc với BC (H thuộc BC)
a, Chứng minh: HB=HC và BAH=CAH
b, Tính độ dài AH
c, Kẻ HD vuông góc với AB (D thuộc AB) , kẻ HE vuông góc với AC (E thuộc AC). Chứng minh tam giác HDE là tam giác cân
Bài 3: Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của CB lấy N sao cho BM=CN
a, Chứng minh: tam giác ABM = tam giác ACN
b, Kẻ BH vuông góc với AM, CK vuông góc với AN( H thuộc AM,K thuộc AN). Chứng minh : AH=AK
c, Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì? Vì sao?
Bài 4: Cho tam giác ABC, kẻ BE vuông góc với AC và CF vuông góc với AB. Biết BE=CF=8 cm. Độ dài các đoạn thẳng BF và BC tỉ lệ với 3 và 5.
a, Chứng minh tam giác ABC là tam giác cân
b, Tính độ dài cạnh đáy BC
c, BE và CF cắt nhau tại O. Nối OA và EF. Chứng minh đường thẳng OA là trung trực của đoạn thẳng EF
Bài 5 : Cho tam giác ABC vuông tại A, BD là tia phân giác của góc ABC (D thuộc AC). Từ D kẻ DE vuông góc với BC tại E. Gọi I là giao điểm của AE và BD. Chứng minh:
a, Tam giác ADB= tam giác EDB
b, BD là đường trung trực của AE
c, Tam giác EDC vuông cân
d, Lấy F thuộc tia đối của tia AB sao cho AF=EC.Chứng minh 3 điểm E, D, F thẳng hàng
Bài 6: Cho tam giác MNP cân tại M. Trên cạnh MN lấy điểm E, trên cạnh MP lấy điểm F sao cho ME=MF. Gọi S là giao điểm của NF và PE. Chứng minh
a, Tam giác MNF= tam giác MPE
b, Tam giác NSE= tam giác PSE
c, EF // NP
d, Lấy K là trung điểm của NP. Chứng minh ba điểm M, S, K thẳng hàng
Bài 7: Cho tam giác ABC vuông tại A. Trên BC lấy E sao cho BE=AB. Qua E kẻ đường thẳng vuông góc với BC cắt AC tại D
a, Chứng minh AD=AE và góc ABD= góc EBD
b, Lấy điểm F thuộc tia đối của tia AB sao cho AF=EC. Chứng minh tam giác DFC cân
c, Gọi O là giao điểm của BD và AE. Chứng minh BD là đường trung trực của AE
d, Chứng minh 3 điểm F, D,E thẳng hàng
Mình đang cần gấp
Theo dõi (0) 1 Trả lời -


1)Cho tam giác ABC vuông tại A có AB=6cm,AC=8cm.
a)Tính độ dài cạnh BC
b)Trên tia BA lấy điểm D sao cho BD=BC.Nối D và C,vẽ đường cao DE của tam giác BDC.CM:tam giác BAC=BED
c)Cm:ABE là Tam giác cân và AE//DC
d)Gọi M là trung điểm của AC.Hai đường thẳng AE và BM cắt nhau tại H.CM: tam giác ACH là tam giác vuông
Theo dõi (1) 1 Trả lời -


cho tam giác ABC có AB =BC, trên cạnh AB lấy điểm M, trên cạnh AC lấy điểm N sao cho AM= AN. Gọi H là trung điểm của BC.
a/ Chứng minh: ^ABH = ^ACH
b/ Gọi E là giao điểm của AH và NM. Chứng minh: ^AME = ^ANE
c/ Chứng minh: MN // BC
(^ Là tam giác)
Theo dõi (0) 1 Trả lời -


Tính góc CMN biết tam giác ABC có góc A=80 độ, AC > AB, D thuộc AC sao cho DC=AB
bởi Nguyễn Hạ Lan
 09/04/2019
09/04/2019
Cho tam giác ABC có Â = 80*, AC > AB. D thuộc AC sao cho DC = AB. M, N là trung điểm AD và BC. Tính góc CMN.
Theo dõi (0) 1 Trả lời -


Chứng minh DE+DF=BH biết tam giác ABC cân tại A có BH vuông góc AC
bởi Phạm Hoàng Thị Trà Giang
 08/04/2019
08/04/2019
1,Cho tam giác ABC cân tại A,kẻ BH vuông góc AC.Gọi D là 1 điểm thuộc cạnh đáy BC.Kẻ DE vuông góc AC; DF vuông góc AB.CMR:DE+DF=BH
2,Cho tam giác ABC có AB>AC.Vẽ AH vuông góc BC.CMR:AB^2-AC^2=HB^2-HC^2
Giúp mk vs ạk.Mấy bài này khó quá
Theo dõi (0) 1 Trả lời -


Chứng minh BE=ED=DC biết tam giác ABC cân tại A có các tia phân giác BD và CE
bởi Naru to
 08/04/2019
08/04/2019
Cho tam giác ABC cân tại A có góc A=80độ
A tính góc B và c
B các tia phân giác BD và CE cắt nhau ở O .CMR :BE=ED=DC
C CMR tam giác OAE =tam giác OAD
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A. Trên cạnh AB, AC lấy D và E sao cho BD = CE. Kẻ DH vuông góc với BC, EK vuông góc với BC. Chứng minh:
a/ Tam giác BDH= tam giác CEK
b/ Tam giác AHK cân
c/ DE//BC
d/ Kẻ AI vuông góc với DE, gọi M là trung điểm của BC. Chứng minh A,I,M thẳng hàng
e/ Trên tia đối tai MA lấy N sao cho MA= MN. Để góc ANC = 30 độ thì tam giác ABC cần điều kiện gì?
Theo dõi (0) 1 Trả lời -


Chứng minh DC vuông góc với BC tại C biết tam giác ABC cân tại A và AB=AD
bởi Nguyễn Sơn Ca
 25/02/2019
25/02/2019
cho tam giác abc cân tại a trên tia đối của tia ba lấy điểm d sao cho AB=AD. CMR DC vuông góc với BC tại C
Theo dõi (0) 1 Trả lời -


Chứng minh A, O, I thẳng hàng biết tam giác ABC cân tại A có góc A < 90 độ
bởi Nguyễn Thủy Tiên
 08/04/2019
08/04/2019
cho tam giác ABC cân tại A có góc A <90o . kẻ BH vuông góc với AC, CK vuông góc với AC. gọi O là giao điểm của BH và CK
a) tam giác ABH= tam giác ACH
b) tam giác BOC cân
c) tam giác OBK=tam giác OCK
d) trên nửa mặt phẳng bờ BC ko chứa điểm A lấy I sao cho IB=IC c/m A,O,I thẳng hàng
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC nhọn. Trên tia đối của tia AB lấy AD=AC, trên tia đối của tia AC lấy AE= AB.
a) Tam giác ACD và tam giác ACE là tam giác gì?
b) Chứng minh CD//BE.
c)Gọi M là trung điểm của BE. Chứng minh AM⊥BE.
d) Kéo dài MA cắt CD ở N. Tính số đo ANC.
Theo dõi (0) 1 Trả lời -


cho tam giác ABC cân tại A ( AB = AC ) D thuộc AB; E thuộc AC sao cho AD= AE. Gọi M là trung điểm của BC
a,Chứng minh DE//BC b, tam giác MBD= tam giác MCE c, tam giác AMD= tam giác AMETheo dõi (0) 1 Trả lời -


Chứng minh tam giác BIC cân biết tam giác ABC cân tại A có BH vuông góc AC
bởi Đặng Ngọc Trâm
 09/04/2019
09/04/2019
Cho tam giác ABC cân tại A(Â<90 độ). Vẽ BH ⊥ AC (H ϵ AC), CK ⊥ AB (K ϵ AB).
a) CM: AH=AK
b) Gọi I là giao điểm BH và CK. CM: tam giác BIC cân
Theo dõi (0) 1 Trả lời -


Cho \(\Delta ABC\) cân tại A \(\left(\widehat{A}< 90^o\right)\).Kẻ \(BD\perp AC\) \(\left(D\in AC\right)\),\(CE\perp AB\left(E\in AB\right)\), BD và CE cắt nhau tại H
a) C/m BD=CE
b)C/m \(\Delta BHC\) cân
c)C/m AH là đường trung trực của BC
d)Trên tia BD lấy điểm K sao cho D là trung điểm của BK. C/m \(\widehat{ECB}=\widehat{DKC}\)
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác IBM cân biết tam giác ABC cân tại A có BP vuông góc AC
bởi Nguyễn Ngọc Sơn
 09/04/2019
09/04/2019
cho \(\Delta\) ABC cân tại A . Gọi M là trung điểm của BC
a. Cm : \(\Delta\) ABM = \(\Delta\) ACM
b. Từ M kẻ MH \(\perp\) AB ( H \(\in\) AB ) và MK \(\perp\) AC ( K \(\in\) AC )
Cm : BH = CK
c. Từ B kẻ BP \(\perp\) AC ( P \(\in\) AC ) biết BP cắt MH tại I
Cm : \(\Delta\) IBM cân
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác CAB cân biết góc xOy < 90 độ và Ot là tia phân giác
bởi Nguyễn Thanh Thảo
 25/02/2019
25/02/2019
Vẽ xOy < 90 độ và tia phân giác Ot. Lấy điểm A thuộc Ox và B thuộc Oy sao cho OA=OB. C là điểm bất kì trên Ot.
a) Chứng minh tam giác CAB cân.
b) OC cắt AB ở D. Tính ADO.
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác AMK cân biết tam giác ABC cân tại A và DM, EK vuông góc BC
bởi Truc Ly
 09/04/2019
09/04/2019
Cho tam giác ABC cân tại A. Trên tia đối BA lấy D trên tia đối của tia CA lấy E sao cho BD=CE vẽ DM và EK cùng vuông góc với BC
a) CM: BM= CK
b) CM: tam giác AMK cân
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABF cân biết tam giác ABC có góc B=60 độ, phân giác BD
bởi Nguyễn Minh Minh
 09/04/2019
09/04/2019
Cho tam giác ABC có góc B= 60 độ, vẽ phân giác BD. từ A kẻ đường thẳng vuồng góc vs BD, cắt BD tại H và cắt BD tại E:
a, Tính số đo góc BAH. Chứng minh tam giác ABE là tam giác đều
b, tam giác DBA= tam giác DBE
c,Từ A kẻ đường tahwngr song song vs BD cắt đường thẳng BC tại F. Chứng minh tam giác ABF là tam giác cânTheo dõi (0) 1 Trả lời -


Ai giúp em với em cần gấp mai phải nộp rồi
Cho tam giác cân ABC có góc a = 100 độ . Tia phân giác của góc B cắt AC tại D . Qua A kẻ đường thẳng vuông góc với BD cắt BC ở I .
a) Chứng minh BA =BI
b) Trên tia đối của tia DB lấy điểm K sao cho DK = DA . Chứng minh tam giác AIK là tam giác đều
c) Tính các góc của tam giác BCK
Mong có người giúp
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC nhọn. Trên tia đối của tia AB, lấy AD=AC, trên tia đối của tia AC lấy AE=AB.
a) So sánh BC và DE. b) Tam giác ACD và tam giác ABE là tam giác gì? c) Gọi M là trung điểm của BE. Chứng minh AM vuông góc BE.Theo dõi (0) 1 Trả lời -


Chứng minh AM//CN biết tam giác ABC vuông tại A có phân giác BH, HM vuông góc BC
bởi Choco Choco
 09/04/2019
09/04/2019
1. Cho tam giác ABC có Â = \(90^0\), AB = 8cm, AC = 6cm.
a, BC = ?
b, Trên cạnh AC lấy điểm E sao cho AE = 2cm, trên tia đối của tia AB lấy điểm D sao cho AB = AD. CM: Tam giác BEC = tam giác DEC.
c, CM: DE đi qua trung điểm cạnh BC.
2. Cho tam giác ABC vuông tại A. Kẻ đường phân giác BH ( H thuộc AC ), kẻ HM vuông góc với BC ( M thuộc BC ). Gọi N là giao điểm của AB và MH. CMR:
a, Tam giác ABH = tam giác MBH
b, BH vuông góc với AM
c, AM // CN
3. Cho tam giác ABC vuông tại A. Đường phân giác BE, kẻ AH vuông góc với BC ( H thuộc BC ). Gọi K là giao điểm của AB và HE. CMR:
a, EA = EH
b, EK = EC
c, BE vuông góc với KC.
Theo dõi (0) 1 Trả lời -


Chứng minh OM vuông góc DE biết M là một điểm thuộc tia phân giác của góc xOy
bởi Van Tho
 09/04/2019
09/04/2019
Cho góc nhọn xOy. Gọi M là một điểm thuộc tia phân giác của góc xOy, kẻ MA vuông góc Ox (A thuộc Ox) ; kẻ MB vuông góc Oy (B thuộc Oy).
a) Chứng minh tam giác OAB cân tại B
b) Đường thẳng BM cắt Ox tại D, đường thẳng AM cắt Oy tại E. Chứng minh rằng: MD = ME
c) Chứng minh: OM vuông góc DE
GIÚP MÌNH VỚI MÌNH SẮP THI RỒI !!!!
Theo dõi (0) 1 Trả lời -


Chứng minh A, D, E thẳng hàng biết 3 tam giác cân ABC, DBC, EBC chung đáy BC
bởi Nguyễn Vân
 09/04/2019
09/04/2019
Cho 3 tam giác cân ABC DBC EBC chung đáy BC.CMR: A,D,E thằng hàng
Theo dõi (0) 1 Trả lời -


Chứng minh BA=BI biết tam giác ABC có AB=AC, góc A=100 độ
bởi A La
 25/02/2019
25/02/2019
Cho tam giác ABC có AB = AC, góc A = 100 độ. Kẻ phân giác BD, kẻ đường vuông góc vs BD từ A cắt BC ở I
a) Chứng minh BA = BI
b) Điểm thuộc tia đối của tia DB sao cho DK = DA. Chứng minh tam giác AIK đều
c) Tính các góc của tam giác BCK
Theo dõi (0) 1 Trả lời -


Tìm điều kiện cho tam giác ABC để tam giác AMC vuông cân biết tam giác ABC vuông tại A
bởi Hương Lan
 09/04/2019
09/04/2019
Cho \(\Delta ABC\) vuông tại A có AB = 8cm, AC = 6cm
a/ Tính BC
b/ Gọi M là trung điểm cạnh BC. Tính độ dài đoạn thẳng AM.
c/ Thêm điều kiện gì cho \(\Delta ABC\) để \(\Delta AMC\) là tam giác vuông cân
Mong các bạn giúp mình câu c và mong các bạn giải chi tiết để cho mình hiểu. Cảm ơn các bạn!
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABD cân và BE vuông góc AD biết tam giác ABC vuông tại A
bởi Nguyễn Trung Thành
 09/04/2019
09/04/2019
Cho tam giác ABC vuông tại A (AB < AC).Có BE là đường phân giác,trên cạnh BC lấy điểm D sao cho BD=BA
a) Chứng minh:tam giác ABD cân và BE ⊥ AD
b) Chứng minh : tam giác BAE=tam giác BDE và EA=ED
c) Trên tia BA lấy điểm F sao cho AF=DC.Chứng minh:EF=EC
d) Chứng minh:F,E,D thẳng hàng
Theo dõi (0) 1 Trả lời -


cho tam giác ABC cân tại A, Â = 100*. Trên tia đối của tia BA lấy điểm E sao cho AE = BC. Tính góc AEC
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABC cân biết trên tia BA lấy D, trên tia đối của tia CA lấy E
bởi Sasu ka
 09/04/2019
09/04/2019
Cho tam giác ABC, trên tia BA lấy D, trên tia đối tia CA lấy E sao cho BD=CE. Qua D kẻ đường thẳng song song AC cắt BC tại F.Gọi I là giao điểm của DE và BC. biết ID=IE. Chứng minh tam giác ABC cân.
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A, tia phân giác góc B cắt AC tại M. Tia phân giác góc C cắt AB tại N.
a) Chứng minh: tam giác AMN cân và MN // BC.
b) Gọi I là trung điểm BC. CM cắt BN tại E. Chứng minh: 3 điểm A,I,E thẳng hàng
Theo dõi (0) 1 Trả lời -


cho tam giác ABC có góc B=2C vẽ AH vuông góc vs BC. gọi M là trung điểm của AC. đường thẳng MH cắt đường thẳng AB tại N. CMR: BN=BH giúp mk nha bài này khó quá
Theo dõi (0) 1 Trả lời -


Chứng minh PC=PA và CM//MN biết tam giác MNP cân tại P và MA vuông PN
bởi Nguyễn Trà Long
 25/02/2019
25/02/2019
Cho \(\Delta MNP\) cân tạị P ( P < 90 độ ), vẽ \(MA\perp PN\) tại A, \(NC\perp PM\) tại C. Chứng minh:
a) PC = PA và CM // MN.
b) Gọi I là giao điểm của MA và NC. Chứng minh: \(\Delta IMN\) cân.
c) Tia PI cắt MN tại K. Chứng minh K là trung điểm của MN.Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N sao cho BM=CN.
a, So sánh Các góc ABM và ACN
b, Chứng minh tam giác AMN cân
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác PIM=tam giác PIN biết tam giác MNP cân tại P, IE vuông PM
bởi truc lam
 25/02/2019
25/02/2019
Cho \(\Delta MNP\) cân tại P. Tia phân giác của góc P cắt MN tại I. Qua I vẽ \(IE\perp PM\) tại E và \(IF\perp PN\) tại F.
a) Chứng minh: \(\Delta PIM=\Delta PIN\)
b) Chứng minh: IE = IF
c) IE cắt PN tại H, IF cắt PM tại K. Chứng minh: \(\Delta PHK\) cân
d) Chứng minh: EF // HKTheo dõi (0) 1 Trả lời -


Tam giác ABC có A= 90 độ. Gọi M là trung điểm của BC. Trên tia đối MA lấy D sao cho MA=MD.
a) CMR: AB song song CD
b) AM=\(\dfrac{1}{2}BC\)
Giúp mk vs mk tik nhanh cho!
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 70 trang 147 SBT Toán 7 Tập 1
Bài tập 71 trang 147 SBT Toán 7 Tập 1
Bài tập 73 trang 147 SBT Toán 7 Tập 1
Bài tập 74 trang 147 SBT Toán 7 Tập 1
Bài tập 75 trang 147 SBT Toán 7 Tập 1
Bài tập 76 trang 147 SBT Toán 7 Tập 1
Bài tập 77 trang 148 SBT Toán 7 Tập 1
Bài tập 78 trang 148 SBT Toán 7 Tập 1
Bài tập 79 trang 148 SBT Toán 7 Tập 1






