Giải bài 41 tr 142 sách BT Toán lớp 7 Tập 1
Hai đoạn thẳng \(AB\) và \(CD\) cắt nhau tại trung điểm \(O\) của mỗi đoạn thẳng. Chứng minh rằng \(AC // BD.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Nếu hai cạnh và góc xen giữa của tam giác này bằng hai cạnh và góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
- Nếu đường thẳng \(c\) cắt hai đường thẳng \(a, b\) và trong các góc tạo thành có một cặp góc so le trong bằng nhau (hoặc cặp góc đồng vị bằng nhau, hoặc cặp góc trong cùng phía bù nhau) thì \(a\) và \(b\) song song với nhau.
Lời giải chi tiết
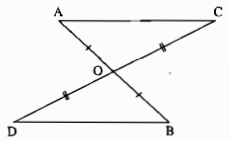
Xét \(∆AOC\) và \(∆BOD\), ta có:
\(OA = OB\) (vì \(O\) là trung điểm của \(AB\))
\(\widehat {AOC} = \widehat {BO{\rm{D}}}\) (đối đỉnh)
\(OC = OD\) (vì \(O\) là trung điểm của \(DC\))
\( \Rightarrow ∆AOC = ∆BOD\) (c.g.c)
\( \Rightarrow \widehat A = \widehat B\) (hai góc tương ứng)
Mà \(\widehat A ;\; \widehat B\) ở vị trí so le trong nên \(AC // BD\) (dấu hiệu nhận biết hai đường thẳng song song).
-- Mod Toán 7 HỌC247
-


Chứng minh OB=OC biết điểm A nằm trong góc nhọn xOy, AH vuông góc với Ox
bởi Đào Lê Hương Quỳnh
 25/04/2019
25/04/2019
Cho điểm A nằm trong góc nhọn xOy. Vẽ AH vuông góc với Ox, trên tia đối của tia HA lấy điểm B sao cho HB=HA. Vẽ AK vuông góc với oy, trên tia đối của KA lấy điểm C sao cho KC=KA.
a/ CM:OB=OC
b/Biết góc xOy=t. Tính góc BOC theo t
c/Tìm số đo của t để O là trung điểm của BC
VẼ HÌNH VÀ GHI LỜI GIẢI RA GIÙM MIK, MIK CẦN GẤP THANKS TRC NHA
Theo dõi (0) 1 Trả lời -


Chứng minh CP//AB và CP=1/2AB biết tam giác ABC có M, N là trung điểm của AB, AC
bởi Lê Nhi
 25/04/2019
25/04/2019
17.Cho tam giác ABC. Gọi M, N thứ tự là trung điểm của AB và AC. Lấy P sao cho N là trung điểm của MP.
CMR:
a)CP//AB và CP=1/2AB
b)Tam giác BMC = tam giác PCM. Từ đó suy ra MN//BC: MN = 1/2BC
Theo dõi (0) 1 Trả lời -


Chứng minh AC vuông góc DC biết tam giác ABC có góc A=90 độ, M là trung điểm BC
bởi sap sua
 25/04/2019
25/04/2019
cho \(\Delta ABC\left(\widehat{A}=90^o\right)\) , M là trung điểm BC , trên tia đối MA lấy D sao cho M là trung điểm AD . C/m
a) \(\Delta AMB=\Delta DMC\)
b) \(DC\perp AC\)
c) AM = \(\frac{1}{2}BC\)
Theo dõi (0) 1 Trả lời -


Chứng minh AC//BE biết tam giác ABC có M là trung điểm BC, trên tia đối của tia MA lấy điểm E
bởi May May
 26/04/2019
26/04/2019
Cho tam giác ABC , M là trung điểm của BC . trên tia đối của tia MA lấy điểm E sao cho ME =MA . CMR:
a, AC= EC và AC // BE
b, Gọi T là 1 điểm trên AC , K là 1 điểm trên EB sao cho AI = EK . CHứng minh ba điểm I, M , K thẳng hàng
c,Từ E kẻ EH vuông góc BC(H thuộc BC).Biết K la trung điêm cua BE.
Làm giúp mk với.Mk đang cần gấp.

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh AC=BD và AC//BD biết 2 đoạn thẳng AB và AD cắt nhau tại trung điểm O của mỗi đoạn
bởi Nguyễn Tiểu Ly
 26/04/2019
26/04/2019
Cho 2 đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn.
a) Chứng minh: AC=BD và AC//BD
b) Chứng minh: AD=BC và AD//BC
c) Gọi M là trung điểm của AC và N là trung điểm của BD. Chứng minh: 3 điểm M, O, N thẳng hàng.
Theo dõi (0) 1 Trả lời -


Tính số đo góc AMB và AMC biết tam giác ABC cân tại A có tia phân giác góc A cắt BC tại M
bởi Nguyễn Trung Thành
 26/04/2019
26/04/2019
Cho tam giác ABC cân tại A. Tia phân giác của góc A cắt BC tại M
b) tính số đo góc AMB và AMC
Theo dõi (0) 1 Trả lời -


cho tam giác ABC vuông tại A. M là trng điểm củaAC
chứng minh rằng: a) KC =AC
b) AK //BC
Theo dõi (0) 1 Trả lời -


Chứng minh nếu tam giác vuông có một góc bằng 30 độ thì cạnh đối diện góc ấy bằng 1 nửa cạnh huyền
bởi sap sua
 26/04/2019
26/04/2019
1 : CMR :
â) Nếu tam giác vuông có một góc bằng 300 thì cạnh đối diện với góc ấy bằng một nửa cạnh huyền .
b) Nếu tam giác vuông có một cạnh góc vuông bằng nửa cạnh huyền thì góc đối diện với cạnh ấy bằng 300.
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông tại A (AB<AC). D là trung điểm BC. Trên tia đối DA lấy M sao cho DA = DM.
a. Chứng minh: Tam giác ABD = Tam giác CMD
b. Chứng minh: AC vuông góc với CM
c. Chứng minh: AC song song BMTheo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (H thuộc BC). Chứng minh rằng:
a) HB=HC
b) góc BAH=góc CAH
Theo dõi (0) 1 Trả lời -


(Ve hinh)cho goc xOy= 60 va diem A nam trong goc xoy ve diem B sao cho Ox la duong trung truc cua AB ve diem C sao cho Oy la duong trung ttuc cua AC
a/ chung minh rang OB = OC
b/ tinh so do BOC
Theo dõi (0) 1 Trả lời -


Chứng minh BE=CD biết tam giác ABC cân tại A, trên tia đối của tia AB lấy điểm D
bởi Phan Thị Trinh
 26/04/2019
26/04/2019
Cho tam giác ABC cân tạiA. Trên tia đối của tia AB lấy điểm D và tia AC lấy điểm E sao cho AD=AE. Chưng minh:
a) DE song song với BC
b) BE=CD
c) Tam giác BED= tam giác CDE
Theo dõi (0) 1 Trả lời -


bài 3: a) cho \(\Delta\)MNP vuông tại N biết MN = 20 cm, MP = 25cm. tìm độ dài cạnh NP
b) cho \(\Delta\)DEF có DE = 10cm, DF= 24cm, EF =26cm. chứng minh \(\Delta\)DEF vuông.
bài 4: cho \(\Delta\)ABC có \(\widehat{A}\)= 90 độ; AB<AC; phân giác BE, E \(\in\) AC. lấy điểm H thuộc cạnh BC sao cho BH= BA. chứng minh:
a) EH\(\perp\)BC
b) BE là đường trung trực của đoạn thẳng AH
c) đường thẳng EH cắt đường thẳng AB ở K. chứng minh EK=EC
d) AH song song với KC
e) gọi M là trung điểm của KC. chứng minh 3 điểm B, E, M thẳng hàng.
Theo dõi (0) 1 Trả lời -


Chứng minh CD=2MG biết tam giác ABC có đường trung tuyến AM và G là trọng tâm tam giác
bởi Bi do
 26/04/2019
26/04/2019
cho tam giác ABC có đg trung tuyến AM và G là trọng tâm tam giác, tia BG cắt AC tại N, trên tia đối của tai NB lấy D sao cho ND=NG.CM tam giác ANG=CND và CD=2MG
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABD=EBD biết tam giác ABC vuông tại A có tia phân giác BD cắt AC tại D
bởi Trần Thị Trang
 26/04/2019
26/04/2019
Cho \(\Delta\) ABC vuông tại A. Tia phân giác của BD cắt AC tại D. Trên cạnh BC lấy điểm E sao cho BE = BA.
a. CM: \(\Delta\) ABD = \(\Delta\) EBD.
b. CM: BD \(\perp\) AE tại H.
c. Qua A kẻ đường thẳng song song với BD cắt đường thẳng ED tại K. CM: \(\Delta\) ADK cân
d. CM: KE < 2AB.
Theo dõi (0) 1 Trả lời -


Chứng minh AM vuông góc BC biết tam giác ABC cân tại A có AB=AC=5cm, BC=3cm
bởi thanh hằng
 26/04/2019
26/04/2019
. Sách toán Vnen lớp 7
. Bài 4: ĐƯỜNG TRUNG TUYẾN CỦA TAM GIÁC. TÍNH CHẤT BA ĐƯỜNG TRUNG TUYẾN CỦA TAM GIÁC.
. C. Hoạt động luyện tập ( Câu 2 nhé )
- Bài 1: Cho tam giác ABC, Trên tia đối của tia BA lấy điểm D sao cho BD = BA. Trên cạnh BC lấy điểm E sao cho BE = \(\dfrac{1}{3}\)BC. Gọi K là giao điểm của AE và CD, Chứng minh rằng DK = KC.
- Bài 2: Cho tam giác ABC cân tại A có AB = AC = 5cm, BC = 3cm. Kẻ trung tuyến AM.
a) Chứng minh rằng AM vuông góc với BC
b) Tính độ dài AM
Help mee. Vẽ hình đầy đủ 2 bài giúp mình nhé. Sau 11h trưa mai nhé mọi người. Trả lời giúp ạ !!!!
Theo dõi (0) 1 Trả lời -


Tính góc ACB biết tam giác ABC vuông tại A có AH vuông góc BC và góc BAH=35 độ
bởi Mai Rừng
 26/04/2019
26/04/2019
Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC ( H thuộc BC ). Trên đường thẳng vuông góc với BC tại B lấy điểm D không cùng nửa mặt phẳng bờ BC với điểm A sao cho BD=AH. Chứng minh rằng:
a) Tam giác AHB bằng tam giác DBH
b) AB//DH
c) Tính góc ACB, biết số đo góc BAH là 35 độ.
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABD=ICE biết tam giác ABC cân có góc A tù, trên BC lấy điểm D
bởi Chai Chai
 26/04/2019
26/04/2019
cho tam giác ABC cân (AB=AC; góc A là góc tù) .trên BC lấy điểm D. trên tia đối của CB lấy điểm E sao cho BD =CE. Trên tia đối của CA lấy điểm I sao cho CI = CA
1/ chứng minh : a) tam giác ABD = tam giác ICE
b) AB+AC < AD+AE
Theo dõi (0) 1 Trả lời -


Chứng minh A, M, N thẳng hàng biết M là trung điểm của BQ, N là trung điểm của CP
bởi Nguyễn Thanh Trà
 26/04/2019
26/04/2019
Cho tam giác ABC có góc B và góc C nhọn. Trên tia đối của tia AB lấy điểm P sao cho AP = AB. Trên tia đối của tia AC lấy điểm Q sao cho AQ = AC.
a, CMR: BQ = CP.
b, Ax là tia bất kì nằm giữa 2 tia AB và AC. Gọi H và K lần lượt là hình chiếu của B và C trên tia Ax. CM: BH + CK nhỏ hơn hoặc bằng BC.
c, Xác định vị trí của tia Ax để tổng Bh + CK có giá trị lớn nhất.
d, Gọi M là trung điểm của BQ, N là trung điểm của CP. CMR: A, M, N thẳng hàng.
Giúp mk câu d thui nha, câu a,b,c mk biết làm rùi!!!
Cách cm câu d:
Đầu tiên CM: góc MAB = góc NAP.
Tiếp theo CM: Góc MAB + góc BAN = 180 độ
Sau đó CM: góc MAN = 180 độ.
Help me!!! Mk cần gấp!!!
Theo dõi (0) 1 Trả lời -


Chứng minh BD vuông góc với AH biết tam giác ABC vuông tại A, BD là tia phân giác của góc ABC
bởi thu hằng
 26/04/2019
26/04/2019
Cho tam giác ABC vuông tại A có AB= 3cm , BC= 5cm
1, tính AC
2, Kẻ BD là tia phân giác của góc ABC ( D thuộc AC). Từ D kẻ DH vuông góc với BC ( H thuộc BC). Chứng minh BD vuông góc với AH
3, Gọi E là giao điểm của DH và AB. Tính AE.
Theo dõi (0) 1 Trả lời -


Giúp mk vs!
CHo tg đều ABC. Trên hai cạnh AC và AC lần lượt lấy hai điểm M và N sao cho AM=CN. Gọi O là giao điểm của CM và BN. CMR:
a) CM=BN
b) Số đó của góc BOC không đổi khi M và N di động trween hai cạnh AC, AB thỏa mãn AM=CN
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ADE cân biết tam giác ABC cân tại A, trên tia đối của tia BC
bởi Long lanh
 26/04/2019
26/04/2019
tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm D , trên tia đối của tia CB lấy điểm E sao cho BD=CE.
a) CMR : tam giác ADE cân
b) Kẻ \(BH\perp AD\left(H\in AD\right),CK\perp AE\left(K\in AE\right)\). CMR BH\(\perp\)CK
c) Gọi O là giao điểm của BH và CK. Tam giác OBC là tam giác gì ? vì sao ?
Theo dõi (0) 1 Trả lời -


Chứng minh BE=CD biết tam giác ABC vuông cân tại A có các tam giác ngoài ABD, ACE đều
bởi Quynh Nhu
 26/04/2019
26/04/2019
Cho tam giác ABC vuông cân tại A. Vẽ ra ngoài tam giác hai tam giác đều ABD và ACE.
a) Chứng minh BE = CD
b) Gọi I là trung điểm BE và CD. Tính góc BIC
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác AMD=AME biết tam giác ABC cân tại A, M là trung điểm BC
bởi Nguyễn Thị Lưu
 26/04/2019
26/04/2019
Cho tam giác ABC cân tại A. Trên các cạnh AB và AC lấy hai điểm tương ứng D và E sao cho AD = AE. Gọi M là trung điểm của BC.
a) Chứng minh DE // BC
b) Chứng minh tam giác MBD = tam giác MCE
c) Chứng minh tam giác AMD = tam giác AME
Theo dõi (0) 1 Trả lời -


Chứng minh BD vuông góc AE biết tam giác ABC nhọn, tia phân giác góc ABC cắt AC tại D
bởi Tran Chau
 05/12/2019
05/12/2019
cho tam giác ABC nhọn (BC>AB). Tia phân giác của góc ABC cắt AC tại D.E thuộc BC: BE=BA
a) CMR: tam giác ABD=EBD.
b) CMR: BD vuông góc với AE
c) Trên nửa mặt phẳng bờ chứa tia AC không chứa B: Kẻ Cx sao cho góc BCA=góc ACx, Cx cắt AB tại F. CMR: góc AFD=CFD
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác AME=tam giác DMB biết tam giác ABC có D là trung điểm của BC
bởi Trần Thị Trang
 05/12/2019
05/12/2019
Cho tam giác ABC. gọi D là trung điểm của BC, M là trung điểm của AD. Trên tia đối của tia MB lấy điểm E sao cho ME = MB
a) chứng minh tam giác AME = tam giác DMB
b) c/m: AE = BD và AE // BC
c) gọi K là giao điểm của DE và AC. c/m tam giác AKE = tam giác CKD
d) trên tia đối của tia MC lấy điểm F sao cho MF = MC. c/m A là trung điểm của EF
lm hộ mk nha
Theo dõi (0) 1 Trả lời -


Chứng minh 3 điểm M, A, N thẳng hàng biết M là trung điểm BC, N trung điểm DE
bởi Lê Tường Vy
 26/04/2019
26/04/2019
cho \(\Delta ABC\) , trên tia đối AC lấy điểm D sao cho AD = AC , trên tia đối AB lấy E sao cho AE = AB nối D với E . C/m
a) \(\Delta ABC=\Delta AED\)
b) BC // DE
c) gọi M là trung điểm BC , N trung điểm DE c/m 3 điểm M , A , N thẳng hàng
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC .Gọi M là trung điểm của BC.Trên tia đối tia MA,lấy điểm D sao cho MA=MD
a)Chứng minh : Tam giác AMB=tam giác DMC
b)Chứng minh AC//BD
c)Trên nửa mp bờ AD ko chứa điểm B vẽ tia Ax//BC. Trên tia Ax lấy điểm H sao cho AH=BC. CM h,c,d thẳng hàng
Theo dõi (0) 1 Trả lời -


Tính số đo góc CDE biết tam giác ABC có góc A=90 độ, trên tia đối của tia CA lấy điểm D
bởi Sasu ka
 26/04/2019
26/04/2019
cho tam giác abc có góc a = 90 độ. trên tia đối tia ca lấy điểm d sao cho cd=ca. trên tia đối tia cb lấy điểm e sao cho ce=cb. tính số đo góc cde
Theo dõi (0) 1 Trả lời -


Chứng minh M là trung điểm của DE biết tam giác ABC có AH vuông góc BC, DE cắt AH ở M
bởi thu thủy
 26/04/2019
26/04/2019
cho ΔABC vẽ AH⊥BC,trên nửa mặt phẳng AH chứa B vẽ AD⊥AB.Sao cho AD=AB trên nửa mặt phẳng còn lại vẽ AE⊥AC,sao cho AE=AC
a)cm DC=BE
b)vẽ EI ⊥AH,DK⊥AH. CM EI=AH,EI=DK
c)DE cắt AH ở M, CM : M là trung điểm của DE
Theo dõi (0) 1 Trả lời -


Chứng minh AM là tia phân giác của góc DAE biết tam giác ABC có AB=AC và M là trung điểm BC
bởi Lê Minh Trí
 26/04/2019
26/04/2019
Cho tam giác ABC có AB=AC và M là trung điểm của BC. Trên tia đối của tia BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE
a) Chứng minh tam giác ABM= tam giác ACM từ đó suy ra AM vuông góc vs BC
b) Chứng minh tam giác ABD= tam giác ACE từ đó suy ra AM là tia phân giác của góc DAE
c) Kẻ BK vuông góc AD( K thuộc AD) trên tia đối của tia BK lấy điểm H sao cho BH=AE, trên tia đối của tia AM lấy điểm N sao cho AN=CE, Chứng minh góc MAD= góc MBH
Theo dõi (0) 1 Trả lời -


Chứng minh H là trung điểm của AB biết trên Ox lấy điểm A,trên Oy lấy điểm B sao cho OA=OB
bởi Bảo Lộc
 26/04/2019
26/04/2019
Cho góc xOy gọi Oz là tia phân giác góc xOy. Trên Ox lấy điểm A,trên Oy lấy điểm B sao cho OA=OB.Lấy điểm I trên Oz (I#0)
- CM: ΔOAI = Δ OBI?
- Đoạn thẳng AB cắt Oz tại H. CM: H là trung điểm của AB?
GIÚP VỚI TỚ ĐANG CẦN GẤP
Theo dõi (0) 1 Trả lời -


So sánh góc OAD và góc OBC biết lấy 1 điểm A trên tia Ox và 1 điểm C trên tia Oy
bởi minh dương
 26/04/2019
26/04/2019
Cho góc nhọn xOy. Ở phía ngoài của góc, vẽ Ox' \(\perp\) Ox, Oy \(\perp\) Oy. Lấy 1 điểm A trên tia Ox và 1 điểm C trên tia Oy. Lấy điểm B trên tia Ox' và điểm D trên tia Oy' sao cho OA=OB, OD=OC
a) So sánh góc AOD và góc BOC
b) CHứng minh AD=BC
c) SO sánh góc OAD và OBC
Theo dõi (0) 1 Trả lời -


Chứng minh góc AEC=góc ADB biết tam giác ABC cân ở có điểm D nằm trong tam giác
bởi Phạm Khánh Linh
 26/04/2019
26/04/2019
Cho tam giác ABC cân ở A có điểm D nằm trong tam giác sao cho góc ADB > ADC. Trên nửa mặt phẳng bờ AC không chứa B, dựng tia Ax sao cho góc CAx = BAD. Trên Ax, lấy điểm E sao cho AE=AD. Chứng minh:
a) góc AEC=ADB
b) góc CED > CDE.
c) DB<DC.
Theo dõi (0) 1 Trả lời -


Chứng minh DH đi qua trung điểm của AC biết tam giác ABC có góc B=2 góc C < 90 độ
bởi Lê Tấn Thanh
 26/04/2019
26/04/2019
Cho \(\Delta ABC\) có \(\widehat{B}=2.\widehat{C}< 90^o\) . Kẻ \(AH\perp BC\) . Trên AB lấy điểm D sao cho AD=HC . CMR : DH đi qua trung điểm của AC.
Theo dõi (0) 1 Trả lời -


Chứng minh AD vuông góc với BC biết tam giác ABC cân tại A, qua B lẻ đường vuông góc với BC
bởi Nguyễn Hạ Lan
 26/04/2019
26/04/2019
Cho tam giác ABC cân tại A. Qua B kẻ đường thẳng vuông góc với BC.Qua C kẻ đường thẳng vuông góc với AC chúng cắt nhau ở D
Chứng minh rằng : a, tam giác BDC cân
b, AD là tia phân giác của A
DA là tia phân giác của D
c, AD vuông góc với BC
Theo dõi (0) 1 Trả lời -


1) Cho tam giác ABC cân tại A . Điểm D \(\in\) AB , E \(\in\) AC sao cho AD= AE , gọi K là giao điểm của BE và CD . C/m
a) BE = CD
b) \(\Delta\)KBD = \(\Delta\) KCE
c) AK là phân giác góc A
d) \(\Delta\) KBC cân
2) Cho tam giác ABC vuông tại A.Gọi M là trung điểm AB. Kẻ MH vuông góc BC tại H . C/m CH\(^2\)= AC\(^2\) + BH\(^2\)
Theo dõi (0) 1 Trả lời -


Chứng minh MD=NE biết tam giác ABC cân tại A, trên cạnh BC lấy điểm D, trên tia đối của tia CB
bởi Hoai Hoai
 26/04/2019
26/04/2019
Cho tam giác ABC cân tại A. Trên cạnh BC lấy điểm D, trên tia đối của tia CB lấy điểm E sao cho BD=CE. Từ D kẻ đường vuông góc với BC cắt AB tại M, từ E kẻ đường vuông góc với BC cắt AC tại N. Cm:
a) MD=NE
b) MN cắt DE ở I. Cm: I là trung điểm của DE.
c) Từ C kẻ đường vuông góc với AC, từ B kẻ đường vuông góc với AB chúng cắt nhau tại O. Cm: AO là đường trung trực của BC
Theo dõi (0) 1 Trả lời -


Chứng minh F là trung điểm của AC biết tam giác ABC có E là trung điểm AB
bởi Lê Nhật Minh
 26/04/2019
26/04/2019
1) Cho \(\Delta\)ABC, \(\widehat{B}\) = 300, AC= \(\frac{BC}{2}\). CMR: \(\widehat{A}\) = 900
2) Cho \(\Delta\)ABC. Gọi E là trung điểm của AB. Qua E kẻ đường thẳng song song với BC, cắt BC tại F. CMR: F là trung điểm của AC
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC cân tại A, trên cạnh BC lần lượt lấy M và N sao cho: BM=MN=NC. H là trung điểm BC.
a, C/m AM=AN và AH vuông góc BC
b, Tính AM khi AB=5, BC=6
c, C/m góc MAN> góc BAM= góc CANTheo dõi (0) 1 Trả lời -


Chứng minh AI vuông góc với BC biết tam giác ABC cân tại A, M và M, N là trung điểm AC, AB
bởi Phan Thị Trinh
 26/04/2019
26/04/2019
Cho tam giác ABC cân tại A.Gọi M,N lần lượt là trung điểm của AC,AB
a) CM: BM=CN và góc ABM=góc ACN
b) Gọi I là giao điểm của BM và CN.Chứng minh tam giác IBC cân
c) CM: AI là tia phân giác của góc A
d) CM: AI vuông góc với BC
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABC=DBC biết tam giác ABC vuông tại A có AH vuông góc BC
bởi Sam sung
 08/05/2019
08/05/2019
Cho \(\Delta ABC\) vuông tại A kẻ \(AH\perp BC\) tại H. Trên tia đối của tia HA lấy điểm D sao cho DH = HA
a) Cho AB=8cm, BC = 10cm. Tính AC
b) Cm \(\Delta ABH=\Delta DBH\) và \(\Delta ABD\) cân
c) Cm \(\Delta ABC=\Delta DBC\)
d) Đường trung trực của BD và đường trung trực của CD cắt nhau tại M Cm M là trung điểm của BC
Theo dõi (0) 1 Trả lời -


Chứng minh AH // BD biết tam giác ABC vuông tại A có góc ABC=30 độ, tia phân giác góc C cắt AB tại E
bởi Long lanh
 08/05/2019
08/05/2019
Cho \(\Delta ABC\)vuông tại A, góc ABC = 300. Tia phân giác của góc C cắt AB tại E. Kẻ EH \(\bot\)BC (H \(\in\)BC)
a) Chứng minh CA = CH; EA = EH
b) Gọi D là giao điểm của CA và HE. Chứng minh: AD = HB
c) Tam giác EBC, AHC, DBC là tam giác gì? Vì sao?
d) Chứng minh: AH // DB
Giúp mk nha ngày 17/02/2017 mk nộp rùi!
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh AI vuông góc BC tại H biết tam giác ABC cân tại A, BC vuông góc với AC
bởi Đan Nguyên
 08/05/2019
08/05/2019
8.Cho tam giác ABC cân tại A, kẻ BC vuông góc với AC và kẻ CE vuông góc với AB, BD và CE cắt nhau tại I.
a/Chứng minh tam giác BDC=tam giác CEB.
b/So sánh góc IBE và góc ICD.
c/Đường thẳng AI cắt BC tại H. Chứng minh AI vuông góc BC tại H.
Theo dõi (0) 1 Trả lời -


cho góc nhọn xOy , gọi Ot là tia phân giác của xOy , lấy điểm M thuộc Ot . Kẻ MA vuông góc OX tại A, kẻ MB vuông góc Oy tại B
1)chứng minh:MA=MB
2)đường thẳng BM cắt tia Ox tại D và đường thẳng AM cắt tia Oy tại E
a) chứng minh:MD=ME
b)chứng minh:OM vuông góc DE
Theo dõi (0) 1 Trả lời -


cho góc nhọn x0y , 0z là tia p/g của x0y , M là điểm bất kì trên tia 0z . kẻ MH vuông góc với 0x tai H , MK vuông góc với 0y tại K
Gọi A , B lần lượt thuộc Ox và Oy sao cho MA = MB.CMR :OA = OB
Giúp mình nhe mình cảm ơn nhiều
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác ABD vuông biết tam giác ABC vuông tại A, đường trung tuyến AM
bởi thanh hằng
 08/05/2019
08/05/2019
Cho \(\triangle{ABC}\) vuông tại A, đường trung tuyến AM. Trên tia đối của tia MA, lấy điểm D sao cho MD = MA.
a) Chứng minh \(\triangle{ABD}\) vuông
b) Chứng minh \(\triangle{ABC}\) = \(\triangle{ABD}\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 39 trang 142 SBT Toán 7 Tập 1
Bài tập 40 trang 142 SBT Toán 7 Tập 1
Bài tập 42 trang 142 SBT Toán 7 Tập 1
Bài tập 43 trang 142 SBT Toán 7 Tập 1
Bài tập 44 trang 143 SBT Toán 7 Tập 1
Bài tập 45 trang 143 SBT Toán 7 Tập 1
Bài tập 46 trang 143 SBT Toán 7 Tập 1





