Phß║¦n hŲ░ß╗øng dß║½n giß║Żi b├Āi tß║Łp SGK H├¼nh hß╗Źc 7 ChŲ░ŲĪng 2 B├Āi 4 TrŲ░ß╗Øng hß╗Żp bß║▒ng nhau thß╗® hai cß╗¦a tam gi├Īc: cß║Īnh - g├│c - cß║Īnh (cgc) sß║Į gi├║p c├Īc em nß║»m ─æŲ░ß╗Żc phŲ░ŲĪng ph├Īp v├Ā r├©n luyß╗ćn k─® n─āng c├Īc dß║Īng b├Āi tß║Łp tß╗½ SGK To├Īn 7 Tß║Łp mß╗Öt.
-
B├Āi tß║Łp 24 trang 118 SGK To├Īn 7 Tß║Łp 1
Vß║Į tam gi├Īc ABC biß║┐t
= 900 AB=AC=3cm. Sau ─æ├│ ─æo c├Īc g├│c B v├Ā C.
-
B├Āi tß║Łp 25 trang 118 SGK To├Īn 7 Tß║Łp 1
Tr├¬n mß╗Śi h├¼nh sau c├│ c├Īc tam gi├Īc n├Āo bß║▒ng nhau? V├¼ sao?
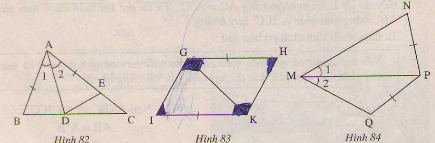
-
B├Āi tß║Łp 26 trang 118 SGK To├Īn 7 Tß║Łp 1
X├®t b├Āi to├Īn:
" Cho tam gi├Īc ABC, M l├Ā trung ─æiß╗ām cß╗¦a BC, Tr├¬n tia ─æß╗æi cß╗¦a MA lß║źy ─æiß╗ām E sao cho ME=MA. Chß╗®ng minh rß║│ng AB//CE'.
DŲ░ß╗øi ─æ├óy l├Ā h├¼nh vß║Į v├Ā giß║Ż thiß║┐t, kß║┐t luß║Łn cß╗¦a b├Āi to├Īn(h.85)
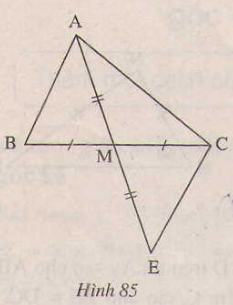

H├Ży sß║»p xß║┐p lß║Īi n─ām c├óu sau ─æ├óy mß╗Öt c├Īch hß╗Żp l├Ł ─æß╗ā giß║Żi b├Āi to├Īn tr├¬n:
1) MB = MC(gt)
=
(Hai g├│c ─æß╗æi ─æß╗ēnh)
MA= ME(Giß║Ż thiß║┐t)
2) Do ─æ├│ ŌłåAMB=ŌłåEMC(c.g.c)
3)
=
=> AB//CE(hai g├│c bß║▒ng nhau ß╗¤ vß╗ŗ tr├Ł sole trong)
4) ŌłåAMB= ŌłåEMC =>
=
(Hai g├│c tŲ░ŲĪng ß╗®ng)
5) ŌłåAMB v├Ā ŌłåEMC c├│:
-
B├Āi tß║Łp 27 trang 119 SGK To├Īn 7 Tß║Łp 1
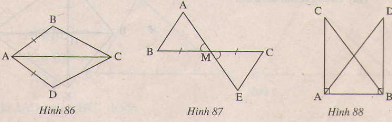
N├¬u th├¬m mß╗Öt ─æiß╗üu kiß╗ćn ─æß╗ā hai tam gi├Īc trong mß╗Śi h├¼nh vß║Į dŲ░ß╗øi ─æ├óy l├Ā hai tam gi├Īc bß║▒ng nhau theo trŲ░ß╗Øng hß╗Żp cß║Īnh-g├│c- cß║Īnh.
a) ŌłåABC= ŌłåADC (h.86);
b) ŌłåAMB= ŌłåEMC (H.87)
c) ŌłåCAB= ŌłåDBA.
-
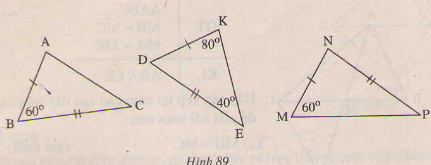
B├Āi tß║Łp 28 trang 120 SGK To├Īn 7 Tß║Łp 1
Tr├¬n h├¼nh 89 c├│ bao nhi├¬u tam gi├Īc bß║▒ng nhau.
-
B├Āi tß║Łp 29 trang 120 SGK To├Īn 7 Tß║Łp 1
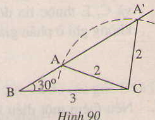
Tr├¬n h├¼nh 90, c├Īc tam gi├Īc ABC va A'B'C' c├│ cß║Īnh chung l├Ā BC=3cm.
CA= CA'= 2cm,
=
nhŲ░ng hai tam gi├Īc ─æ├│ kh├┤ng bß║▒ng nhau.
Tß║Īi sao ß╗¤ ─æ├óy kh├┤ng thß║┐ ├Īp d├╣ng trŲ░ß╗Øng hß╗Żp c.g.c ─æß╗ā kß║┐t luß║Łn hai tam gi├Īc bß║▒ng nhau.
-
B├Āi tß║Łp 30 trang 120 SGK To├Īn 7 Tß║Łp 1
Tr├¬n h├¼nh 90, c├Īc tam gi├Īc ABC v├Ā A'BC c├│ cß║Īnh chung BC= 3cm cß║Īnh chung BC = 3cm, CA=CA'= 2cm,
=
= 300nhŲ░ng hai tam gi├Īc ─æ├│ kh├┤ng bß║▒ng nhau.
Tß║Īi sao ß╗¤ ─æ├óy kh├┤ng ├Īp dß╗źng trŲ░ß╗Øng hß╗Żp cß║Īnh g├│c cß║Īnh ─æß╗ā kß║┐t luß║Łn ŌłåABC=ŌłåA'B 'C'?
-
B├Āi tß║Łp 31 trang 120 SGK To├Īn 7 Tß║Łp 1
Cho ─æß╗Ö d├Āi ─æoß║Īn thß║│ng AB, ─æiß╗ām nß║▒m tr├¬n ─æŲ░ß╗Øng trung trß╗▒c cß╗¦a AB, so s├Īnh ─æß╗Ö d├Āi c├Īc ─æoß║Īn MA,MB.
-
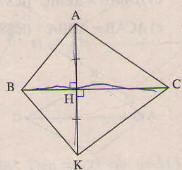
B├Āi tß║Łp 32 trang 120 SGK To├Īn 7 Tß║Łp 1
T├¼m c├Īc tia ph├ón gi├Īc tr├¬n h├¼nh 91. H├Ży chß╗®ng minh ─æiß╗üu ─æ├│.
-
B├Āi tß║Łp 36 trang 142 SBT To├Īn 7 Tß║Łp 1
Vß║Į tam gi├Īc \(ABC\) biß║┐t \(BA = BC = 2,5cm\), \(\widehat B = 90^\circ \). Sau ─æ├│ ─æo c├Īc g├│c \(A\) v├Ā \(C\) ─æß╗ā kiß╗ām tra rß║▒ng \(\widehat A = \widehat C = 45^\circ \)
-
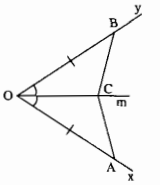
B├Āi tß║Łp 37 trang 142 SBT To├Īn 7 Tß║Łp 1
Dß╗▒a v├Āo h├¼nh \(53\), h├Ży n├¬u ─æß╗ü to├Īn chß╗®ng minh \(ŌłåAOC = ŌłåBOC\) theo trŲ░ß╗Øng hß╗Żp cß║Īnh ŌĆō g├│c ŌĆō cß║Īnh.
-
B├Āi tß║Łp 38 trang 142 SBT To├Īn 7 Tß║Łp 1
Qua trung ─æiß╗ām \(I\) cß╗¦a ─æoß║Īn thß║│ng \(AB\), kß║╗ ─æŲ░ß╗Øng vu├┤ng g├│c vß╗øi \(AB\), tr├¬n ─æŲ░ß╗Øng vu├┤ng g├│c ─æ├│ lß║źy hai ─æiß╗ām \(C\) v├Ā \(D.\) Nß╗æi \(CA, CB, DA, DB.\) T├¼m ca╠üc cß║Ęp tam gi├Īc bß║▒ng nhau trong h├¼nh vß║Į.
-
B├Āi tß║Łp 39 trang 142 SBT To├Īn 7 Tß║Łp 1
Vß║Į \( ŌłåABC\) c├│ \(\widehat A = 90^\circ \), \(AB = 3cm, AC = 1cm.\) Sau ─æ├│ ─æo g├│c \(C\) ─æß╗ā kiß╗ām tra rß║▒ng \(\widehat C \approx 72^\circ \).
-
B├Āi tß║Łp 40 trang 142 SBT To├Īn 7 Tß║Łp 1
Qua trung ─æiß╗ām \(M\) cß╗¦a ─æoß║Īn thß║│ng \(AB\), kß║╗ ─æŲ░ß╗Øng thß║│ng vu├┤ng g├│c vß╗øi \(AB.\) Tr├¬n ─æŲ░ß╗Øng thß║│ng ─æ├│ lß║źy ─æiß╗ām \(K.\) Chß╗®ng minh rß║▒ng \(KM\) l├Ā tia ph├ón gi├Īc cß╗¦a g├│c \(AKB.\)
-
B├Āi tß║Łp 41 trang 142 SBT To├Īn 7 Tß║Łp 1
Hai ─æoß║Īn thß║│ng \(AB\) v├Ā \(CD\) cß║»t nhau tß║Īi trung ─æiß╗ām \(O\) cß╗¦a mß╗Śi ─æoß║Īn thß║│ng. Chß╗®ng minh rß║▒ng \(AC // BD.\)
-
B├Āi tß║Łp 42 trang 142 SBT To├Īn 7 Tß║Łp 1
Cho tam gi├Īc \(ABC\) c├│ \(\widehat A = 90^\circ \). Tr├¬n tia ─æß╗æi cß╗¦a tia \(CA\) lß║źy ─æiß╗ām \(D\) sao cho \(CD = CA\), Tr├¬n tia ─æß╗æi cß╗¦a tia \(CB\) lß║źy ─æiß╗ām \(E\) sao cho \(CE = CB.\) T├Łnh sß╗æ ─æo g├│c \(CDE.\)
-
B├Āi tß║Łp 43 trang 142 SBT To├Īn 7 Tß║Łp 1
Cho tam gi├Īc \(ABC\) c├│ \(\widehat A = 90^\circ \), tr├¬n cß║Īnh \(BC\) lß║źy ─æiß╗ām \(E\) sao cho \(BE = BA.\) Tia ph├ón gi├Īc cß╗¦a g├│c \(B\) cß║»t \(AC\) ß╗¤ \(D.\)
a) So s├Īnh c├Īc ─æß╗Ö d├Āi \(DA\) v├Ā \(DE.\)
b) T├Łnh sß╗æ ─æo g├│c \(BED.\)
-
B├Āi tß║Łp 44 trang 143 SBT To├Īn 7 Tß║Łp 1
Cho tam gi├Īc \(AOB\) c├│ \(OA = OB.\) Tia ph├ón gi├Īc cß╗¦a g├│c \(O\) cß║»t \(AB\) ß╗¤ \(D.\) Chß╗®ng minh rß║▒ng:
a) \(DA = DB\)
b) \(O{\rm{D}} \bot\, AB\)
-
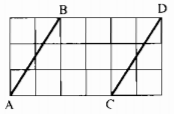
B├Āi tß║Łp 45 trang 143 SBT To├Īn 7 Tß║Łp 1
Cho c├Īc ─æoß║Īn thß║│ng AB v├Ā CD tr├¬n giß║źy kß║╗ ├┤ vu├┤ng (h├¼nh dŲ░ß╗øi). Chß╗®ng minh rß║▒ng AB = CD, AB // CD.
-
B├Āi tß║Łp 46 trang 143 SBT To├Īn 7 Tß║Łp 1
Cho tam gi├Īc \(ABC\) c├│ ba g├│c nhß╗Źn. Vß║Į ─æoß║Īn thß║│ng \(AD\) vu├┤ng g├│c vß╗øi \(AB\) v├Ā bß║▒ng \(AB\) (\(D\) kh├Īc ph├Ła \(C\) ─æß╗æi vß╗øi \( AB\)), vß║Į ─æoß║Īn thß║│ng \(AE \) vu├┤ng g├│c vß╗øi \(AC\) v├Ā bß║▒ng \(AC\) (\(E\) kh├Īc ph├Ła \(B\) ─æß╗æi vß╗øi \(AC\))
Chß╗®ng minh rß║▒ng:
a) \(DC = BE\)
b) \({\rm{D}}C \bot\, BE\)
-
B├Āi tß║Łp 47 trang 143 SBT To├Īn 7 Tß║Łp 1
Cho tam gi├Īc \(ABC\) c├│ \(\widehat B = 2\widehat C\). Tia ph├ón gi├Īc cß╗¦a g├│c \(B\) cß║»t \(AC\) ß╗¤ \(D\). Tr├¬n tia ─æß╗æi cß╗¦a tia \(BD\) lß║źy ─æiß╗ām \(E\) sao cho \(BE = AC.\) Tr├¬n tia ─æß╗æi cß╗¦a tia \(CB\) lß║źy ─æiß╗ām \(K\) sao cho \(CK = AB.\) Chß╗®ng minh rß║▒ng \(AE = AK\).
-
B├Āi tß║Łp 48 trang 143 SBT To├Īn 7 Tß║Łp 1
Cho tam gi├Īc \(ABC\), \(K\) l├Ā trung ─æiß╗ām cß╗¦a \(AB, E\) l├Ā trung ─æiß╗ām cß╗¦a \(AC.\) Tr├¬n tia ─æß╗æi cß╗¦a tia \(KC\) lß║źy ─æiß╗ām \(M\) sao cho \(KM = KC.\) Tr├¬n tia ─æß╗æi cß╗¦a tia \(EB\) lß║źy ─æiß╗ām \(N\) sao cho \(EN = EB.\) Chß╗®ng minh r─ā╠Ćng \(A\) l├Ā trung ─æiß╗ām cß╗¦a \(MN.\)






