Hình học 12 Ôn tập chương 3 Phương pháp toạ độ trong không gian

Lý thuyết10 Trắc nghiệm94 BT SGK 643 FAQ

Cùng điểm lại nội dung chương Phương pháp tọa độ trong không gian bằng sơ đồ tư duy sẽ giúp các em hệ thống lại kiến thức, ghi nhớ dễ dàng những nội dung trọng tâm. Bên cạnh đó là những bài tập tổng hợp nâng cao sẽ giúp các em rèn luyện kĩ năng làm bài tập và từng bước chinh phục được bài toán khó.

YOMEDIA

1. Tóm tắt lý thuyết

1.1. Sơ đồ các dạng toán viết phương trình đường thẳng, mặt phẳng, mặt cầu

1.2. Sơ đồ các công thức định lượng của phương pháp tọa độ trong không gian

2. Bài tập minh hoạ

3. Luyện tập Ôn tập Chương 3 Hình học 12

3.1 Trắc nghiệm

3.2 Bài tập SGK

4. Hỏi đáp về Ôn tập Chương 3 Hình học 12

Tóm tắt lý thuyết

1.1. Sơ đồ các dạng toán viết phương trình đường thẳng, mặt phẳng, mặt cầu

Sơ đồ các dạng phương trình đường và mặt trong không gian

1.2. Sơ đồ các công thức định lượng của phương pháp tọa độ trong không gian

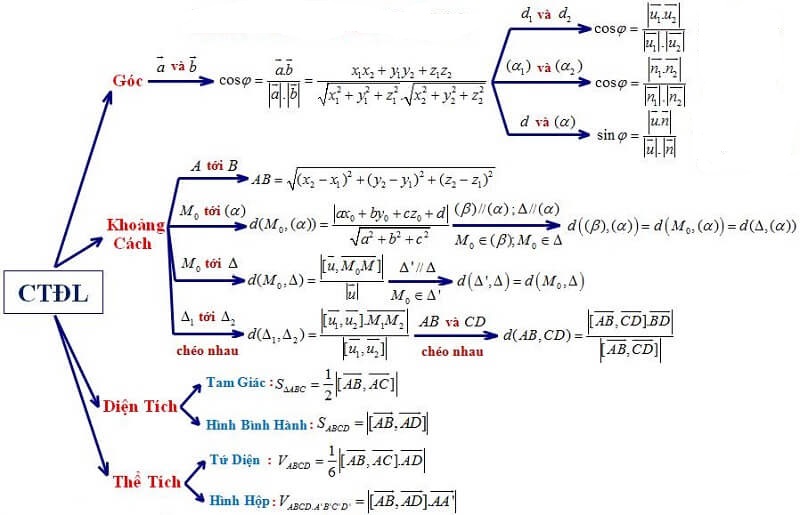
Sơ đồ các công thức tính góc, khoảng cách, diện tích, thể tích trong không gian

Bài tập minh họa

Bài tập 1:

Trong không gian với hệ tọa độ Oxyz , cho A(0;-3;-1) và B(-4;1;-3) và mặt phẳng \((P):x-2y+2z-7=0\).
a) Viết phương trình mặt phẳng (Q) đi qua gốc tọa độ, song song với AB và vuông góc với (P).
b) Lập phương trình mặt cầu nhận đoạn thẳng AB là đường kính.

Lời giải:

a) Ta có \(\overrightarrow{AB}=(-4;4;-2),\vec{n}=(1;-2;2)\) là véc tơ pháp tuyến của mặt phẳng (P).
\(\left [ \overrightarrow{AB};\vec{n} \right ]=(4;6;4)\)
(Q) là mặt phẳng đi qua gốc tọa độ O(0;0;0), (Q) song song với AB và vuông góc với mặt phẳng (P) suy ra mặt phẳng (Q) nhận \(\overrightarrow {{n_{(Q)}}} = \frac{1}{2}\left[ {\overrightarrow {AB} ;\vec n} \right] = (2;3;2)\) làm véctơ pháp tuyến.
Vậy phương trình mặt phẳng (Q) là: \(2x+3y+2z=0.\)
b. \(\overrightarrow{AB}=(-4;4;-2)\Rightarrow AB=\sqrt{16+16+4}=6\)
Trung điểm AB là I(-2;-1;-2).
Mặt cầu (S) có tâm I, bán kính \(R=\frac{AB}{2}=3\Rightarrow (S):(x+2)^2+(y+1)^2+(z+2)^2=9\).

Bài tập 2:

Cho mặt cầu \((S): x^2+y^2+z^2-2x+6y+4z-22=0\) và \((\alpha ):x+2y-2z-8=0\). CRM: \((\alpha )\) cắt (S) theo một đường tròn. Xác định tâm, bán kính đường tròn đó.

Lời giải:

Tâm đường tròn giao tuyến của mặt cầu S(I;R) và \((\alpha )\) là hình chiếu của I trên \((\alpha )\) với \(r^2+d^2(I;(\alpha ))=R^2\).

\((S): (x-1)^2+(y+3)^2+(z+2)^2=36\)

Mặt cầu (S) có tâm I(1;-3;-2), bán kính R = 6.
\(d(I;(\alpha ))=\frac{\left | 1-6+4-8 \right |}{\sqrt{1^2+2^2+(-2)^2}}=\frac{9}{3}=3\) Vậy \((\alpha )\) cắt mặt cầu theo 1 đường tròn.

Xác định tâm của H của đường tròn giao tuyến

Ta có H là hình chiếu của I trên \((\alpha )\).
Đường thẳng \(\Delta\) đi qua I và vuông góc với \((\alpha )\), tức là nhận \(\vec{n_\alpha }=(1;2;-2)\) làm một VTCP có phương trình là:
\(\Delta \left\{\begin{matrix} x=1+t\\ y=-3+2t\\ z=-2-2t \end{matrix}\right.\)
\(H =\Delta \cap (\alpha )\)
\(H\in \Delta \Rightarrow H(1+t;-3+2t;-2-2t)\)
\(H\in (\alpha ) \Rightarrow 1+t+2(-3+2t)-2(-2-2t)-8=0\)
\(\Leftrightarrow 9t-9=0\Leftrightarrow t=1\)
Suy ra tọa độ H(2;-1;-4).

Bán kính đường trình giao tuyến: \(r^2=R^2-IH^2=36-9=27.\)

Vậy \(r=3\sqrt{3}.\)

3. Luyện tập Ôn tập Chương 3 Hình học 12

3.1 Trắc nghiệm

Để củng cố bài học xin mời các em cùng làm Bài kiểm tra Trắc nghiệm Ôn tập chương III - Hình học 12 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

Câu 1:
Trong không gian với hệ tọa độ Oxyz, cho ba điểm \(A\left( {1; - 1;1} \right);B\left( {2;1; - 2} \right),C\left( {0;0;1} \right).\) Gọi \(H\left( {x;y;z} \right)\) là trực tâm của tam giác ABC. Tính giá trị của \(Q = x + y + z.\)
- A. \(Q=1\)
- B. \(Q=\frac{1}{3}\)
- C. \(Q=2\)
- D. \(Q=3\)
Câu 2:
Trong không gian với hệ trục Oxyz, cho đường thẳng \(\left( d \right):x - 1 = \frac{{y - 2}}{2} = \frac{{z - 4}}{3}\) và song song với mặt phẳng \(\left( P \right):x + 4y + 9z - 9 = 0.\) Tìm giao điểm I của (d ) và (P).
- A. I(2;4;-1)
- B. I(1;2;0)
- C. I(1;0;0)
- D. I(0;0;1)
Câu 3:
Trong không gian với hệ trục Oxyz, tìm tọa độ hình chiếu vuông góc của điểm A(0;1;2) trên mặt phẳng \(\left( P \right):x + y + z = 0.\)
- A. (-1;0;1)
- B. (-2;0;2)
- C. (-1;1;0)
- D. (-2;2;0)

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

3.2 Bài tập SGK

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Ôn tập chương III - Hình học 12 sẽ giúp các em nắm được các phương pháp giải bài tập từ SGK Hình học 12 Cơ bản và Nâng cao.

Bài tập 1 trang 91 SGK Hình học 12

Bài tập 2 trang 91 SGK Hình học 12

Bài tập 3 trang 92 SGK Hình học 12

Bài tập 4 trang 92 SGK Hình học 12

Bài tập 5 trang 92 SGK Hình học 12

Bài tập 6 trang 92 SGK Hình học 12

Bài tập 7 trang 92 SGK Hình học 12

Bài tập 8 trang 93 SGK Hình học 12

Bài tập 9 trang 93 SGK Hình học 12

Bài tập 10 trang 93 SGK Hình học 12

Bài tập 11 trang 93 SGK Hình học 12

Bài tập 12 trang 93 SGK Hình học 12