Giải bài 12 tr 93 sách GK Toán Hình lớp 12
Tìm tọa độ điểm A' đối xứng với điểm A(1; -2; -5) qua đường thẳng có phương trình:
\(\left\{\begin{matrix} x=1+2t\\ y=-1-t\\ z=2t \end{matrix}\right.\)
Hướng dẫn giải chi tiết bài 12
Phương pháp:
Để tìm điểm A' đối xứng với A qua đường thẳng \(\Delta\) ta thực hiện các bước sau:
- Tìm tọa độ hình chiếu vuông góc của A lên \(\Delta\):
- Viết phương trình mặt phẳng \(\left ( \alpha \right )\) đi qua A và vuông góc với \(\Delta\).
- Tìm giao điểm H của \(\left ( \alpha \right )\) và \(\Delta\).
- Điểm H vừa tìm được chính là trung điểm của A và A'.
Lời giải:
Ta có lời giải chi tiết bài 12 như sau:
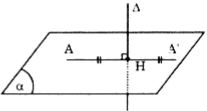
Đường thẳng \(\Delta\) có vecto chỉ phương \(\vec{a}=(2;-1;2)\)
Gọi \((\alpha )\) là mặt phẳng qua A và vuông góc với \(\Delta\) thì \((\alpha )\) có vecto pháp tuyến \(\vec{n}=\vec{a}=(2;-1;2)\) do đó phương trình mp\((\alpha )\) là:
\(2(x-1)-(y+2)+2(z+5)=0\)
\(\Leftrightarrow 2x-y+2z+6=0\) (1)
Hình chiếu H của A lên \(\Delta\) là giao điểm của \(\Delta\) và \((\alpha )\).
Thay x = 1 + 2t, y = -1 - t, z = 2t vào (1) ta được:
\(2(1+2t)-(-1-t)+4t+6=0\Leftrightarrow 9t+9=0\Leftrightarrow t=-1\)
Khi đó x = -1, y = 0; z = -2
Vậy H(-1; 0; -2)
Vì A' là điểm đối xứng của A qua \(\Delta\) nên:
\(\overrightarrow {AA'} = 2\overrightarrow {AH} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {{x_{A'}} - 1 = 2( - 1 - 1)}\\ {{y_{A'}} + 2 = 2(0 + 2)}\\ {{z_{A'}} + 5 = 2.( - 2 + 5)} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {{x_{A'}} = - 3}\\ {{y_{A'}} = 2}\\ {{z_{A'}} = 1} \end{array}} \right.\)
Vậy điểm đối xứng với A qua đường thẳng \(\Delta\) là A'(-3; 2; 1).
-- Mod Toán 12 HỌC247
-


Hãy lập phương trình mặt phẳng (P) đi qua điểm I(-1; -1; 1) và chứa đường thẳng d: \(\dfrac{{x + 2}}{{ - 1}} = \dfrac{{y - 1}}{4} = \dfrac{{z - 1}}{{ - 1}}\).
bởi Dang Tung
 25/05/2021
25/05/2021
Hãy lập phương trình mặt phẳng (P) đi qua điểm I(-1; -1; 1) và chứa đường thẳng d: \(\dfrac{{x + 2}}{{ - 1}} = \dfrac{{y - 1}}{4} = \dfrac{{z - 1}}{{ - 1}}\).
Theo dõi (0) 1 Trả lời -


Hãy lập phương trình mặt phẳng (P) chứa hai đường thẳng: \(d:\left\{ {\begin{array}{*{20}{c}}{x = - 2 - t}\\{y = 1 + 4t}\\{z = 1 - t}\end{array}} \right.\) và \(d':\left\{ {\begin{array}{*{20}{c}}{x = - 1 + t'}\\{y = - 3 + 4t'}\\{z = 2 - 3t'}\end{array}} \right.\)
bởi Nguyễn Trà Long
 24/05/2021
24/05/2021
Hãy lập phương trình mặt phẳng (P) chứa hai đường thẳng: \(d:\left\{ {\begin{array}{*{20}{c}}{x = - 2 - t}\\{y = 1 + 4t}\\{z = 1 - t}\end{array}} \right.\) và \(d':\left\{ {\begin{array}{*{20}{c}}{x = - 1 + t'}\\{y = - 3 + 4t'}\\{z = 2 - 3t'}\end{array}} \right.\)
Theo dõi (0) 1 Trả lời -


Hãy lập phương trình mặt phẳng (P) đi qua ba điểm A(-1; -3; 2), B(-2; 1; 1) và C(0; 1; -1).
bởi lê Phương
 24/05/2021
24/05/2021
Hãy lập phương trình mặt phẳng (P) đi qua ba điểm A(-1; -3; 2), B(-2; 1; 1) và C(0; 1; -1).
Theo dõi (0) 1 Trả lời -


Lập phương trình mặt phẳng (P) đi qua M(1; -3; 2) và song song với mặt phẳng \((Q): x – z = 0\).
bởi Trung Phung
 24/05/2021
24/05/2021
Lập phương trình mặt phẳng (P) đi qua M(1; -3; 2) và song song với mặt phẳng \((Q): x – z = 0\).
Theo dõi (0) 1 Trả lời -


Hãy lập phương trình mặt phẳng (P) đi qua điểm M(1; -3; 2) và vuông góc với đường thẳng d: \(\dfrac{{x - 3}}{2} = \dfrac{{y + 1}}{{ - 1}} = \dfrac{z}{3}\).
bởi het roi
 24/05/2021
24/05/2021
Hãy lập phương trình mặt phẳng (P) đi qua điểm M(1; -3; 2) và vuông góc với đường thẳng d: \(\dfrac{{x - 3}}{2} = \dfrac{{y + 1}}{{ - 1}} = \dfrac{z}{3}\).
Theo dõi (0) 1 Trả lời -


Trong không gian \(M\left( { - \dfrac{{29}}{3};\dfrac{{26}}{3}; - \dfrac{7}{3}} \right)\), cho mặt phẳng \(M\left( {\dfrac{{11}}{3};\dfrac{{14}}{3}; - \dfrac{{13}}{3}} \right)\) : \((S)\)và điểm \(I(3; - 2;1)\). Phương trình mặt cầu tâm \(I\)và tiếp xúc với mặt phẳng \((P)\) là đáp án?
bởi Xuan Xuan
 06/05/2021
06/05/2021
A.\(d(I;(P)) = 6 < R\).
B.\((P)\).
C.\((S)\).
Theo dõi (0) 1 Trả lời -


Trong không gian \(B\left( {\dfrac{1}{3}; - \dfrac{1}{3}; - \dfrac{1}{3}} \right)\), cho mặt cầu \(d(A,(P)) = 5 \ge d(B,(P)) = 1.\) có tâm \( \Rightarrow d(A,(P)) \ge d(M,(P)) \ge d(B,(P)).\) tiếp xúc với mặt phẳng \( \Rightarrow d{(M,(P))_{\min }} = 1 \Leftrightarrow M \equiv B.\). Mặt cầu \(Oxyz\) có bán kính \(2x - 2y - z + 9 = 0\) bằng:
bởi Nguyễn Thị Trang
 06/05/2021
06/05/2021
A.\(M\).
B.\((S):{(x - 3)^2} + {(y + 2)^2} + {(z - 1)^2} = 100\).
C.\((S)\).
D.\(M\).
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 10 trang 93 SGK Hình học 12
Bài tập 11 trang 93 SGK Hình học 12
Bài tập 1 trang 94 SGK Hình học 12
Bài tập 2 trang 94 SGK Hình học 12
Bài tập 3 trang 94 SGK Hình học 12
Bài tập 4 trang 94 SGK Hình học 12
Bài tập 5 trang 95 SGK Hình học 12
Bài tập 6 trang 95 SGK Hình học 12
Bài tập 7 trang 95 SGK Hình học 12
Bài tập 8 trang 95 SGK Hình học 12
Bài tập 9 trang 95 SGK Hình học 12
Bài tập 10 trang 95 SGK Hình học 12
Bài tập 11 trang 96 SGK Hình học 12
Bài tập 12 trang 96 SGK Hình học 12
Bài tập 13 trang 96 SGK Hình học 12
Bài tập 14 trang 97 SGK Hình học 12
Bài tập 15 trang 97 SGK Hình học 12
Bài tập 3.46 trang 131 SBT Hình học 12
Bài tập 3.47 trang 131 SBT Hình học 12
Bài tập 3.48 trang 131 SBT Hình học 12
Bài tập 3.49 trang 132 SBT Hình học 12
Bài tập 3.50 trang 132 SBT Hình học 12
Bài tập 3.51 trang 132 SBT Hình học 12
Bài tập 3.52 trang 132 SBT Hình học 12
Bài tập 3.53 trang 132 SBT Hình học 12
Bài tập 3.54 trang 132 SBT Hình học 12
Bài tập 3.56 trang 132 SBT Hình học 12
Bài tập 3.57 trang 132 SBT Hình học 12
Bài tập 3.58 trang 132 SBT Hình học 12
Bài tập 3.59 trang 133 SBT Toán 12
Bài tập 3.60 trang 133 SBT Toán 12
Bài tập 3.61 trang 133 SBT Toán 12
Bài tập 3.62 trang 133 SBT Toán 12
Bài tập 3.63 trang 133 SBT Toán 12
Bài tập 3.64 trang 133 SBT Toán 12
Bài tập 3.65 trang 133 SBT Toán 12
Bài tập 3.66 trang 134 SBT Toán 12
Bài tập 3.67 trang 134 SBT Toán 12
Bài tập 3.68 trang 134 SBT Toán 12
Bài tập 3.69 trang 134 SBT Toán 12
Bài tập 3.70 trang 134 SBT Toán 12
Bài tập 3.71 trang 134 SBT Toán 12
Bài tập 1 trang 114 SGK Hình học 12 NC
Bài tập 2 trang 114 SGK Hình học 12 NC
Bài tập 3 trang 114 SGK Hình học 12 NC
Bài tập 4 trang 114 SGK Hình học 12 NC
Bài tập 5 trang 114 SGK Hình học 12 NC
Bài tập 6 trang 114 SGK Hình học 12 NC
Bài tập 7 trang 114 SGK Hình học 12 NC
Bài tập 8 trang 115 SGK Hình học 12 NC
Bài tập 9 trang 115 SGK Hình học 12 NC
Bài tập 10 trang 115 SGK Hình học 12 NC
Bài tập 11 trang 115 SGK Hình học 12 NC
Bài tập 12 trang 116 SGK Hình học 12 NC
Bài tập 13 trang 116 SGK Hình học 12 NC
Bài tập 14 trang 116 SGK Hình học 12 NC
Bài tập 15 trang 116 SGK Hình học 12 NC
Bài tập 16 trang 116 SGK Hình học 12 NC
Bài tập 17 trang 117 SGK Hình học 12 NC
Bài tập 18 trang 117 SGK Hình học 12 NC
Bài tập 19 trang 117 SGK Hình học 12 NC
Bài tập 20 trang 118 SGK Hình học 12 NC
Bài tập 21 trang 118 SGK Hình học 12 NC
Bài tập 22 trang 118 SGK Hình học 12 NC
Bài tập 23 trang 118 SGK Hình học 12 NC
Bài tập 24 trang 118 SGK Hình học 12 NC
Bài tập 25 trang 119 SGK Hình học 12 NC
Bài tập 26 trang 119 SGK Hình học 12 NC
Bài tập 27 trang 119 SGK Hình học 12 NC
Bài tập 28 trang 120 SGK Hình học 12 NC
Bài tập 29 trang 120 SGK Hình học 12 NC
Bài tập 30 trang 121 SGK Hình học 12 NC
Bài tập 31 trang 121 SGK Hình học 12 NC
Bài tập 32 trang 121 SGK Hình học 12 NC
Bài tập 33 trang 121 SGK Hình học 12 NC
Bài tập 34 trang 122 SGK Hình học 12 NC
Bài tập 35 trang 122 SGK Hình học 12 NC
Bài tập 36 trang 122 SGK Hình học 12 NC
Bài tập 37 trang 123 SGK Hình học 12 NC
Bài tập 38 trang 123 SGK Hình học 12 NC
Bài tập 39 trang 123 SGK Hình học 12 NC
Bài tập 40 trang 124 SGK Hình học 12 NC





