Bài tập 36 trang 122 SGK Hình học 12 NC
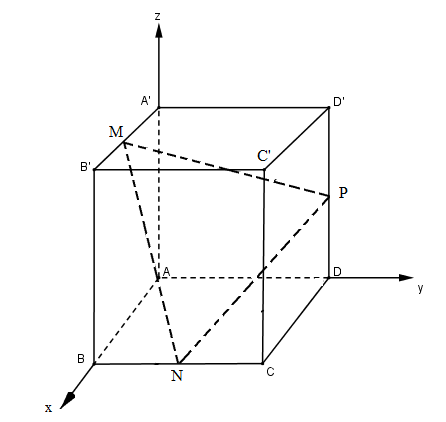
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Gọi M, N, P lần lượt là trung điểm của A’B’, BC, DD’. Chứng minh rằng \(AC' \bot \left( {MNP} \right).\)
Một học sinh làm như sau:
Bước 1: Chọn hệ trục tọa độ như hình 71;
Khi đó A(0; 0; 0), C’(1; 1; 1),
\(M = \left( {\frac{1}{2};0;1} \right),N\left( {1;\frac{1}{2};0} \right),P\left( {0;1;\frac{1}{2}} \right).\)
Bước 2:
\(\begin{array}{l}
\overrightarrow {AC'} = \left( {1;1;1} \right),\overrightarrow {MN} = \left( {\frac{1}{2};\frac{1}{2}; - 1} \right)\\
\overrightarrow {MP} = \left( { - \frac{1}{2};1; - \frac{1}{2}} \right).
\end{array}\)
Bước 3:
\(\left\{ \begin{array}{l}
\overrightarrow {AC\prime } .\overrightarrow {MN} = 0\\
\overrightarrow {AC\prime } .\overrightarrow {MP} = 0
\end{array} \right. \Rightarrow AC\prime \bot (MNP).\)
Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào?
(A) Đúng
(B) Sai ở bước 1
(C) Sai ở bước 2
(D) Sai ở bước 3
Hướng dẫn giải chi tiết
Bài toán trên giải đúng
Chọn (A).
-- Mod Toán 12 HỌC247
-
Viết phương trình mặt cầu (S) có bán kính bằng \(\frac{MN}{6}\), tâm nằm trên đường thẳng MN và (S) tiếp xúc với (P)
bởi Phan Quân
07/02/2017
Trong không gian với hệ tọa độ Oxyz, cho hai điểm M(1;-2;3), N(- 1;0;1) và mặt phẳng (P): x + y + z + 4 = 0. Viết phương trình mặt cầu (S) có bán kính bằng \(\frac{MN}{6}\), tâm nằm trên đường thẳng MN và (S) tiếp xúc với (P).
Theo dõi (0) 2 Trả lời -
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(2; 4; -1), B(1; 4; 1), C(2; 4; 1), D(2; 2; -1).
a) Viết phương trình mặt cầu (S) có tâm A(2; 4; -1) và đi qua điểm B(1; 4; 1)
b) Tính góc giữa hai véc tơ \(\overrightarrow{AB}\) và \(\overrightarrow{CD}\)
Theo dõi (0) 2 Trả lời -
Viết phương trình đường thẳng d nằm trong mặt phẳng (P) đồng thời cắt và vuông góc với đường thẳng AB
bởi Truc Ly
08/02/2017
Trong không gian hệ Oxyz, cho hai điểm A(0 ; 0; -3), B( 2; 0; -1) và mặt phẳng (P) có phương trình 3x – 4y + z – 1 =0. Tìm tọa độ giao điểm của đường thẳng AB với mặt phẳng (P). Viết phương trình đường thẳng d nằm trong mặt phẳng (P) đồng thời cắt và vuông góc với đường thẳng AB.
Theo dõi (0) 1 Trả lời -
Trong không gian với hệ trục tọa độ Oxyz, cho mặt phẳng (P): \(x+y+2z-3=0\) và hai điểm A (2;1;3); B (6; -7;8) . Tìm tọa độ điểm M thuộc mặt phẳng (P) sao cho MA + MB đạt giá trị nhỏ nhất.
Theo dõi (0) 2 Trả lời -
Tìm tọa độ điểm A thuộc d sao cho khoảng cách từ A đến (P) bằng \(2\sqrt{3}\).
bởi Co Nan
07/02/2017
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng \((P): x+y+z-3=0\) và đường thẳng \(d: \frac{x-2}{1}=\frac{y+1}{-2}=\frac{z}{-1}\). Tìm tọa độ giao điểm của (P) và d; tìm tọa độ điểm A thuộc d sao cho khoảng cách từ A đến (P) bằng \(2\sqrt{3}\).
Theo dõi (0) 1 Trả lời -
Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(4;2;2), B(0;0;7) và đường thẳng \(d: \frac{x-3}{-2}=\frac{y-6}{2}=\frac{z-1}{1}\). Chứng minh rằng hai đường thẳng d và AB cùng thuộc một mặt phẳng. Tìm điểm C thuộc đường thẳng d sao cho tam giác ABC cân đỉnh A.
Theo dõi (0) 1 Trả lời -
Viết phương trình mặt cầu (S) có tâm thuộc đường thẳng d và tiếp xúc với mặt phẳng (Oxy)
bởi Mai Thuy
08/02/2017
Trong không gian tọa độ Oxyz, cho mặt phẳng \((\alpha ):2x-y+2z+1=0\) và đường thẳng \(d: \frac{x-1}{1}=\frac{y-1}{2}=\frac{z}{-2}\) . Viết phương trình mặt cầu (S) có tâm thuộc đường thẳng d và tiếp xúc với mặt phẳng (Oxy) và mặt phẳng \((\alpha )\).
Theo dõi (0) 2 Trả lời
