YOMEDIA

Ôn tập Toán 12 Chương 3 Nguyên Hàm - Tích Phân & Ứng Dụng

HỌC247 xin gửi đến các em học sinh lớp 12 tài liệu Ôn tập Toán 12 Chương 3 về Nguyên hàm, Tích phân và Ứng dụng, nhằm giúp các em hệ thống lại kiến thức của toàn bộ các bài đã học thông qua các sơ đồ, cùng với đó là các bảng tra cứu nhanh nguyên hàm các hàm số quen thuộc sẽ giúp các em ghi nhớ bài học tốt hơn. Ngoài ra, các em có thể xem chi tiết nội dung của từng bài học và hướng dẫn giải chi tiết bài tập SGK. Tài liệu còn bổ sung phần trắc nghiệm online cùng một số đề kiểm tra 1 tiết nhằm giúp các em có thể tự luyện tập, làm quen với cấu trúc đề thi. Chúc các em ôn tập hiệu quả và đạt thành tích cao trong học tập.

YOMEDIA

Đề cương Ôn tập Toán 12 Chương 3

A. Tóm tắt lý thuyết 

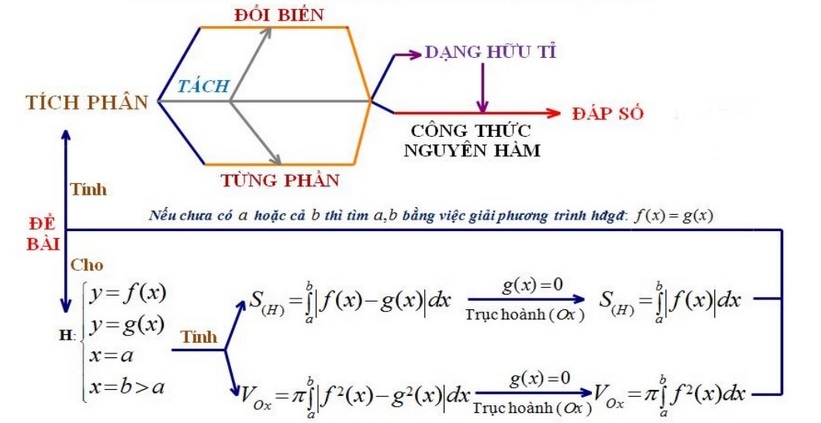
1. Sơ đồ chung các bài toán tích phân và ứng dụng

Sơ đồ tư duy các bài toán tích phân

2. Bảng công thức nguyên hàm của một số hàm số

\(\int {0dx = C;\int {dx = x + C} } \) \(\int {\frac{{dx}}{{{a^2} + {x^2}}} = \frac{1}{a}\arctan \frac{x}{a} + C\left( {a > 0} \right)} \)
\(\int {{{\left( {ax + b} \right)}^\alpha }dx = \frac{1}{a}\frac{{{{\left( {ax + b} \right)}^{\alpha  + 1}}}}{{\alpha  + 1}} + C,\alpha  \ne  - 1} \) \(\int {\frac{{dx}}{{{a^2} - {x^2}}}}  = \frac{1}{{2a}}\ln \left| {\frac{{a + x}}{{a - x}}} \right| + C\)
\(\int {\frac{1}{{ax + b}}dx = \frac{1}{a}\ln \left| {ax + b} \right| + C} \) \(\int {{\rm{cos}}\left( {ax + b} \right)dx = \frac{1}{a}\sin \left( {ax + b} \right) + C} \)
\(\int {{e^{ax + b}}dx = \frac{1}{a}{e^{ax + b}} + C} \) \(\int {\sin \left( {ax + b} \right)dx =  - \frac{1}{a}{\rm{cos}}\left( {ax + b} \right) + C} \)
\(\int {{m^{ax + b}}dx = \frac{1}{{a\ln m}}{m^{ax + b}} + C} \) \(\int {\tan \left( {ax + b} \right)dx}  =  - \frac{1}{a}\ln \left| {{\rm{cos}}\left( {ax + b} \right)} \right| + C\)
\(\int {\ln \left( {ax + b} \right)dx = \left( {x + \frac{b}{a}} \right)\ln \left( {ax + b} \right) - x + C} \) \(\int {\cot \left( {ax + b} \right)dx = \frac{1}{a}\ln \left| {\sin \left( {ax + b} \right)} \right| + C} \)
\(\int {\frac{{dx}}{{\sqrt {{a^2} - {x^2}} }} = \arcsin \frac{x}{a} + C\left( {a > 0} \right)} \) \(\int {\frac{1}{{{{\sin }^2}\left( {ax + b} \right)}}dx =  - \frac{1}{a}\cot \left( {ax + b} \right) + C} \)
\(\int {\frac{{dx}}{{\sqrt {a + {x^2}} }} = \ln \left| {x + \sqrt {{x^2} + a} } \right| + C} \) \(\int {\frac{1}{{{{\cos }^2}\left( {ax + b} \right)}}dx = \frac{1}{a}\tan \left( {ax + b} \right) + C} \)

3. Các dạng nguyên hàm từng phần và cách chọn u, dv

Nguyên hàm \(u\)

\(dv\)
\(\int P \left( x \right).\sin \left( {ax + b} \right)dx\) \(P(x)\) \(\sin \left( {ax + b} \right)dx\)
\(\int P \left( x \right).\cos \left( {ax + b} \right)dx\) \(P(x)\) \(\cos \left( {ax + b} \right)dx\)
\(\int {P\left( x \right).{m^{ax + b}}dx} \) \(P(x)\) \({m^{ax + b}}dx\)
\(\int {P\left( x \right).{{\log }_m}\left( {ax + b} \right)dx} \) \({\log _m}\left( {ax + b} \right)\) \(P(x)dx\)
\(\int {{x^k}\sin \left( {{{\log }_a}x} \right)dx} \) \(\sin \left( {{{\log }_a}x} \right)\) \({x^k}dx\)
\(\int {{x^k}\cos \left( {{{\log }_a}x} \right)dx} \) \(\cos \left( {{{\log }_a}x} \right)\) \({x^k}dx\)
\(\int {{m^{ax + b}}\sin \left( {\alpha x + \beta } \right)dx} \) \({m^{ax + b}}\) \({\sin \left( {\alpha x + \beta } \right)dx}\)
\(\int {{m^{ax + b}}\cos \left( {\alpha x + \beta } \right)} dx\) \({m^{ax + b}}\) \({\cos \left( {\alpha x + \beta } \right)} dx\)

4. Các dạng nguyên hàm vô tỉ và các phép đổi biến số lượng giác hóa

Dạng nguyên hàm Đổi biến số Điều kiện biến số
\(1.\int {f\left( {x,\sqrt {{a^2} - {x^2}} } \right)dx} \) \(x = a.\sin t\) \(t \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right]\)
\(2.\int {f\left( {x,\sqrt {{x^2} - {a^2}} } \right)dx} \) \(x = \frac{a}{{\cos t}}\) \(t \in \left[ {0;\frac{\pi }{2}} \right) \cup \left[ {\pi ;\frac{{3\pi }}{2}} \right)\)
\(3.\int {f\left( {x,\sqrt {{a^2} + {x^2}} } \right)} dx\) \(x = a.\tan t\) \(t \in \left[ {0;\frac{\pi }{2}} \right)\)
\(4.\int {f\left( {x,\sqrt {\frac{{a + x}}{{a - x}}} } \right)dx} \) \(x = a.\cos 2t\) \(t \in \left( {0;\frac{\pi }{2}} \right)\)
\(5.\int {f\left( {x,\sqrt {\left( {x - a} \right)\left( {b - x} \right)} } \right)dx} \) \(x = a + \left( {b - a} \right){\sin ^2}t\) \(t \in \left[ {0;\frac{\pi }{2}} \right]\)

B. Bài tập minh họa

Bài 1: Tìm các nguyên hàm sau:

a) \(I = \int\limits {\left( {3x + 1} \right)\left( {x - 2} \right)} \,dx\).

b) \(J = \int\limits {\left( {5{{\sin }^2}x - \sin x + 2} \right)\cos x} \,dx\).

Hướng dẫn giải

a) \(I = \int\limits {\left( {3x + 1} \right)\left( {x - 2} \right)} \,dx\)

\(I = \int\limits {\left( {3{x^2} - 5x - 2} \right)} \,dx = {x^3} - \frac{{5{x^2}}}{2} - 2x + C.\)

b) \(J = \int\limits {\left( {5{{\sin }^2}x - \sin x + 2} \right)\cos x} \,dx\)

Đặt: \(t = \sin x \Rightarrow dt = \cos xdx\) 

Khi đó: \(J = \int\limits {\left( {5{t^2} - t + 2} \right)} \,dt = \frac{{5{t^3}}}{3} - \frac{{{t^2}}}{2} + 2t + C = \frac{5}{3}{\sin ^3}x - \frac{{{{\sin }^2}x}}{2} + 2\sin x + C.\)

Bài 2: Tính các tích phân sau:

a)  \(I=\int_{1}^{3}x(3x+2lnx)dx.\)

b)  \(I=\int_{1}^{2}\frac{x^2+ln^2x}{x}dx.\)

c) \(I = \int\limits_{\frac{{\sqrt 2 }}{2}}^1 {\frac{{\sqrt {1 - {x^2}} }}{{{x^2}}}dx} .\)

Hướng dẫn giải

a) \(I=\int_{1}^{2}3x^2dx+\int_{1}^{2}2xlnxdx\)
Đặt \(I_1=\int_{1}^{2}3x^2dx; I_2=\int_{1}^{2}2xlnxdx\)
\(I_1=\int_{1}^{2}3x^2dx=x^3\bigg |^2_1=7.\)
\(I_2=\int_{1}^{2}lnxd(x^2)=(x^2lnx)\bigg|^2_1-\int_{1}^{2}xdx=4ln2- \frac{x^2}{2}\bigg|^2_1=4ln2-\frac{3}{2}.\)
Vậy \(I=I_1+I_2=4ln2-\frac{11}{2}.\)

b) Ta tách tích phân I như sau: \(I=\int_{1}^{2}\frac{x^2+ln^2x}{x}dx=\int_{1}^{2}xdx+\int_{1}^{2}\frac{ln^2x}{x}dx\)
\(I_1=\int_{1}^{2}xdx=\frac{x^2}{2}\bigg|^2_1=\frac{3}{2}\)
\(I_2=\int_{1}^{2}\frac{ln^2x}{x}dx\)
Đặt \(t=lnx\Rightarrow dt=\frac{1}{x}dx\)
Đổi cận: \(x=2\Rightarrow t=ln2;x=1\Rightarrow t=0\)
\(I_2=\int_{0}^{ln2}t^2dt=\frac{t^3}{3}\bigg |^{ln2}_0=\frac{ln^32}{3}\)
Vậy \(I=I_1+I_2=\frac{3}{2}+\frac{ln^32}{3}.\)

c) \(I = \int\limits_{\frac{{\sqrt 2 }}{2}}^1 {\frac{{\sqrt {1 - {x^2}} }}{{{x^2}}}dx} .\)

Đặt \(x = \cos t,t \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right] \Rightarrow dx = - \sin tdt\)

Đổi cận: \(\left\{ \begin{array}{l} x = \frac{{\sqrt 2 }}{2} \Rightarrow t = \frac{\pi }{4}\\ x = 1 \Rightarrow t = 0 \end{array} \right.\)

Khi đó: 

\(\begin{array}{l} I = - \int\limits_{\frac{\pi }{4}}^0 {\frac{{\sqrt {1 - {{\cos }^2}t} .\sin t}}{{{{\cos }^2}t}}dt} = \int\limits_0^{\frac{\pi }{4}} {\frac{{\left| {\sin t} \right|.\sin t}}{{{{\cos }^2}t}}dt} \\ = \int\limits_0^{\frac{\pi }{4}} {\left( {\frac{1}{{{{\cos }^2}t}} - 1} \right)dt} = \left. {\left( {\tan t - t} \right)} \right|_0^{\frac{\pi }{4}} = 1 - \frac{\pi }{4}. \end{array}\)

Bài 3: Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số y = x2 + x, trục hoành và hai đường thẳng x = 0, x = 1.

Hướng dẫn giải

Diện tích hình phẳng cần tính là: \(S=\int_{0}^{1}\left | x^2+x \right |dx\)
Với \(x\in [0;1]\Rightarrow S=\int_{0}^{1}(x^2+x)dx\)
Suy ra \(S=(\frac{x^3}{3}+\frac{x^2}{2})\bigg |^1_0=\frac{5}{6}.\)
Vậy \(S=\frac{5}{6}\).

Bài 4: Cho hình phẳng giới hạn bởi các đường \(y = \frac{1}{{1 + \sqrt {4 - 3{\rm{x}}} }},y = 0,x = 0,x = 1\) quay quanh trục Ox. Tính thể tích V của khối tròn xoay tạo thành.

Hướng dẫn giải

Thể tích cần tìm: \(V = \pi \int\limits_0^1 {\frac{{dx}}{{{{\left( {1 + \sqrt {4 - 3x} } \right)}^2}}}}\)

Đặt: \(t = \sqrt {4 - 3x} \Rightarrow dt = - \frac{3}{{2\sqrt {4 - 3x} }}dx \Leftrightarrow dx = - \frac{2}{3}tdt\left( {x = 0 \Rightarrow t = 2;x = 1 \Rightarrow t = 1} \right)\)

Khi đó: 

\(\begin{array}{l} V = \frac{{2\pi }}{3}\int\limits_1^2 {\frac{t}{{{{\left( {1 + t} \right)}^2}}}dt} = \frac{{2\pi }}{3}\int\limits_1^2 {\left( {\frac{1}{{1 + t}} - \frac{1}{{{{\left( {1 + t} \right)}^2}}}} \right)dt} \\ = \left. {\frac{{2\pi }}{3}\left( {\ln \left| {1 + t} \right| + \frac{1}{{1 + t}}} \right)} \right|_1^2 = \frac{\pi }{9}\left( {6\ln \frac{3}{2} - 1} \right). \end{array}\)

Trắc nghiệm Toán 12 Chương 3

Đề kiểm tra Toán 12 Chương 3

Đề kiểm tra trắc nghiệm online Chương 3 Toán 12 (Thi Online)

Phần này các em được làm trắc nghiệm online để kiểm tra năng lực và sau đó đối chiếu kết quả và xem đáp án chi tiết từng câu hỏi.

Đề kiểm tra Chương 3 Toán 12 (Tải File)

Phần này các em có thể xem online hoặc tải file đề thi về tham khảo gồm đầy đủ câu hỏi và đáp án làm bài.

Lý thuyết từng bài Chương 3 và hướng dẫn giải bài tập SGK

Lý thuyết các bài học Toán 12 Chương 3

Hướng dẫn giải bài tập Toán 12 Chương 3

Trên đây là tài liệu Ôn tập Toán 12 Chương 3. Hy vọng với tài liệu này, các em sẽ giúp các em ôn tập và hệ thống lại kiến thức Chương 3 thật tốt. Để thi online và tải file đề thi về máy các em vui lòng đăng nhập vào trang hoc247.net và ấn chọn chức năng "Thi Online" hoặc "Tải về". Ngoài ra, các em còn có thể chia sẻ lên Facebook để giới thiệu bạn bè cùng vào học, tích lũy thêm điểm HP và có cơ hội nhận thêm nhiều phần quà có giá trị từ HỌC247 !       

AANETWORK
 

XEM NHANH CHƯƠNG TRÌNH LỚP 12

 

ATNETWORK
ON