Phần hướng dẫn giải bài tập Ôn tập chương III - Hình học 12 Ôn tập chương III - Hình học 12 sẽ giúp các em nắm được phương pháp và rèn luyện kĩ năng các giải bài tập từ SGK Hình học 12 Cơ bản và Nâng cao.
-
Bài tập 1 trang 91 SGK Hình học 12
Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1), D(-2; 1; -1)
a) Chứng minh A, B, C, D là bốn đỉnh của một tứ diện.
b) Tìm góc giữa hai đường thẳng AB và CD
c) Tính độ dài đường cao của hình chóp A.BCD
-
Bài tập 2 trang 91 SGK Hình học 12
Cho mặt cầu (S) có đường kính là AB biết rằng A(6; 2; -5), B(-4; 0; 7)
a) Tìm tọa độ tâm I và bán kính r của mặt cầu (S).
b) Lập phương trình của mặt cầu (S).
c) Lập phương trình của mặt phẳng (\(\alpha\)) tiếp xúc với mặt cầu (S) tại điểm A.
-
Bài tập 3 trang 92 SGK Hình học 12
Cho bốn điểm A(-2; 6; 3), B(1; 0; 6), C(0; 2; -1), D(1; 4; 0)
a) Viết phương trình mặt phẳng (BCD). Suy ra ABCD là một tứ diện.
b) Tính chiều cao AH của tứ diện ABCD.
c) Viết phương trình mặt phẳng (\(\alpha\)) chứa AB và song song với CD.
-
Bài tập 4 trang 92 SGK Hình học 12
Lập phương trình tham số của đường thẳng:
a) Đi qua hai điểm A(1;0;-3), B(2;-1;0)
b) Đi qua điểm M(2;3;-5) và song song với đường thẳng \(\Delta\) có phương trình: \(\left\{\begin{matrix} x=-2+2t\\ y=3-4t\\ z=-5t \end{matrix}\right.\)
-
Bài tập 5 trang 92 SGK Hình học 12
Cho mặt cầu (S) có phương trình (x – 3)2 + (y + 2)2 + (z – 1)2 = 100 và mặt phẳng \((\alpha )\) có phương trình 2x – 2y – z + 9 = 0. Mp \((\alpha )\) cắt mặt cầu (S) theo một đường tròn (C). Hãy xác định tọa độ tâm và tính bán kính của đường tròn (C).
-
Bài tập 6 trang 92 SGK Hình học 12
Cho mặt phẳng \((\alpha )\) có phương trình 3x + 5y - z - 2 = 0 và đường thẳng d có phương trình: \(\left\{\begin{matrix} x=12+4t\\ y=9+3t\\ z=1+t \end{matrix}\right.\)
a) Tìm giao điểm M của đường thẳng d và mặt phẳng \((\alpha )\).
b) Viết phương trình mặt phẳng \((\beta )\) chứa điểm M và vuông góc với đường thẳng d.
-
Bài tập 7 trang 92 SGK Hình học 12
Cho điểm A(-1;2;-3), vecto \(\vec{a}=(6;-2;-3)\) và đường thẳng d có phương trình: \(\left\{\begin{matrix} x=1+3t\\ y=-1+2t\\ z=3-5t \end{matrix}\right.\)
a) Viết phương trình mặt phẳng (\(\alpha\)) chứa điểm A và vuông góc với \(\vec a.\)
b) Tìm giao điểm của d và (\(\alpha\)).
c) Viết phương trình đường thẳng \(\Delta\) đi qua điểm A, vuông góc với \(\vec{a}\) và cắt đường thẳng d.
-
Bài tập 8 trang 93 SGK Hình học 12
Viết phương trình mặt phẳng \((\alpha )\) tiếp xúc với mặt cầu
\((S): x^2+y^2+z^2-10x+2y+26z+170=0\)
và song song với hai đường thẳng \(d:\left\{\begin{matrix} x=-5+2t\\ y=1-3t\\ z=-13+2t \end{matrix}\right.;d':\left\{\begin{matrix} x=-7+3t\\ y=-1-2t\\ z=8 \end{matrix}\right.\)
-
Bài tập 9 trang 93 SGK Hình học 12
Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M(1; -1; 2) trên mặt phẳng \((\alpha )\): 2x – y + 2z + 11 = 0.
-
Bài tập 10 trang 93 SGK Hình học 12
Cho điểm M(2; 1; 0) và mặt phẳng \((\alpha )\): x + 3y – z – 27 = 0. Tìm tọa độ điểm M' đối xứng với M qua \((\alpha )\).
-
Bài tập 11 trang 93 SGK Hình học 12
Viết phương trình đường thẳng \(\Delta\) vuông góc với mặt phẳng toạ độ (Oxz) và cắt hai đường thẳng: \(d:\left\{\begin{matrix} x=t\\ y=-4+t\\ z=3-t \end{matrix}\right.; d':\left\{\begin{matrix} x=1-2t\\ y=-3+t\\ z=4-5t \end{matrix}\right.\)
-
Bài tập 12 trang 93 SGK Hình học 12
Tìm tọa độ điểm A' đối xứng với điểm A(1; -2; -5) qua đường thẳng có phương trình:
\(\left\{\begin{matrix} x=1+2t\\ y=-1-t\\ z=2t \end{matrix}\right.\)
-
Bài tập 1 trang 94 SGK Hình học 12
Trong không gian với hệ tọa độ Oxyz, cho ba vectơ \(\overrightarrow a = ( - 1;1;0);\overrightarrow b = \left( {1;1;0} \right);\overrightarrow c = \left( {1;1;1} \right).\)
Trong các mệnh đề sau, mệnh đề nào sai?
(A) \(\left | \vec{a} \right |=\sqrt{2}\)
(B) \(\left | \vec{c} \right |=\sqrt{3}\)
(C) \(\vec{a}\perp \vec{b}\)
(D) \(\vec{b}\perp \vec{c}\)
-
Bài tập 2 trang 94 SGK Hình học 12
Trong không gian với hệ tọa độ Oxyz, cho ba vectơ \(\overrightarrow a = ( - 1;1;0);\overrightarrow b = \left( {1;1;0} \right);\overrightarrow c = \left( {1;1;1} \right).\)
Trong các mệnh đề sau, mệnh đề nào đúng?
(A) \(\vec{a}.\vec{c}=1\)
(B) \(\vec{a},\vec{b}\) cùng phương
(C) \(cos(\vec{b},\vec{c})=\frac{2}{\sqrt{6}}\)
(D) \(\vec{a}+\vec{b}+\vec{c}=\vec{0}\)
-
Bài tập 3 trang 94 SGK Hình học 12
Trong không gian \(Oxyz\) cho ba vectơ \(\overrightarrow a = ( - 1;1;0)\), \(\overrightarrow b = (1;1;0)\) và \(\overrightarrow c = (1;1;1)\)
Cho hình bình hành \(OADB\) có \(\overrightarrow {OA} \) = \(\overrightarrow a \), \(\overrightarrow {OB} = \overrightarrow b \) (\(O\) là gốc toạ độ). Toạ độ của tâm hình bình hành \(OADB\) là:
(A) \((0 ; 1 ; 0)\)
(B) \((1 ; 0 ; 0)\)
(C) \((1 ; 0 ; 1)\)
(D) \((1 ; 1 ; 0)\).
-
Bài tập 4 trang 94 SGK Hình học 12
Trong không gian \(Oxyz\) cho bốn điểm \(A(1; 0; 0), B(0; 1; 0), C(0; 0; 1)\) và \(D(1; 1; 1)\)
Trong các mệnh đề sau, mệnh đề nào sai?
(A) Bốn điểm A, B, C, D tạo thành một tứ diện ;
(B) Tam giác ABD là tam giác đều ;
(C) \(AB ⊥ CD\) ;
(D) Tam giác \(BCD\) là tam giác vuông.
-
Bài tập 5 trang 95 SGK Hình học 12
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1;0;0); B(0;1;0); C(0;0;1); D(1;1;1).
Gọi M, N lần lượt là trung điểm của AC và CD. Toạ độ điểm G là trung điểm của MN là:
(A) \(G\left ( \frac{1}{3} ; \frac{1}{3}; \frac{1}{3}\right )\)
(B) \(G\left ( \frac{1}{4} ; \frac{1}{4}; \frac{1}{4}\right )\)
(C) \(G\left ( \frac{2}{3};\frac{2}{3};\frac{2}{3} \right )\)
(D) \(G\left ( \frac{1}{2};\frac{1}{2};\frac{1}{2} \right )\)
-
Bài tập 6 trang 95 SGK Hình học 12
Trong không gian với hệ tọa độ Oxyz, cho bốn điểm A(1;0;0); B(0;1;0); C(0;0;1); D(1;1;1).
Mặt cầu ngoại tiếp tứ diện ABCD có bán kính là:
(A) \(\frac{\sqrt{3}}{2}\)
(B) \(\sqrt{2}\)
(C) \(\sqrt{3}\)
(D) \(\frac{3}{4}\)
-
Bài tập 7 trang 95 SGK Hình học 12
Cho mặt phẳng \((\alpha )\) đi qua điểm M(0;0;-1) và song song với giá của hai vecto \(\vec{a}=(1;-2;3)\) và \(\vec{b}=(3;0;5)\).
Phương trình của mặt phẳng \((\alpha )\) là:
(A) 5x - 2y - 3z - 21 = 0
(B) -5x + 2y + 3z + 3 = 0
(C) 10x - 4y - 6z + 21 = 0
(D) 5x - 2y - 3z + 21 = 0
-
Bài tập 8 trang 95 SGK Hình học 12
Cho ba điểm A(0; 2; 1), B(3; 0; 1), C(1; 0; 0). Phương trình mặt phẳng (ABC) là:
(A) 2x – 3y – 4z + 2 = 0
(B) 2x + 3y – 4z – 2 = 0
(C) 4x + 6y – 8z + 2 = 0
(D) 2x – 3y – 4z + 1 = 0
-
Bài tập 9 trang 95 SGK Hình học 12
Gọi \((\alpha )\) là mặt phẳng cắt ba trục toạ độ tại ba điểm M(8; 0; 0), N(0; -2; 0), P(0; 0; 4). Phương trình của \((\alpha )\) là:
(A) \(\frac{x}{8}-\frac{y}{-2}+\frac{z}{4}=0\)
(B) \(\frac{x}{4}+\frac{y}{-1}+\frac{z}{2}=0\)
(C) \(x-4y+2z=0\)
(D) \(x-4y+2z-8=0\)
-
Bài tập 10 trang 95 SGK Hình học 12
Cho ba mặt phẳng
\((\alpha ): x+y+2z+1=0\)
\((\beta ): x+y-z+2=0\)
\((\gamma): x-y+5=0\)
Trong các mệnh đề sau, mệnh đề nào sai?
(A) \((\alpha )\perp (\beta )\)
(B) \((\gamma )\perp (\beta )\)
(C) \((\alpha ) // (\gamma )\)
(D) \((\alpha ) \perp (\gamma )\)
-
Bài tập 11 trang 96 SGK Hình học 12
Cho đường thẳng \(\Delta\) đi qua điểm M(2; 0; -1) và có vecto chỉ phương \(\vec{a}=(4;-6;2)\). Phương trình tham số của đường thẳng \(\Delta\) là:
(A) \(\left\{\begin{matrix} x=-2+4t\\ y=-6t\\ z=1+2t \end{matrix}\right.\)
(B) \(\left\{\begin{matrix} x=-2+2t\\ y=-3t\\ z=1+t \end{matrix}\right.\)
(C) \(\left\{\begin{matrix} x=2+2t\\ y=-3t\\ z=-1+t \end{matrix}\right.\)
(D) \(\left\{\begin{matrix} x=4+2t\\ y=-6-3t\\ z=2+t \end{matrix}\right.\)
-
Bài tập 12 trang 96 SGK Hình học 12
Cho d là đường thẳng đi qua điểm A(1;2;3) và vuông góc với mặt phẳng \((\alpha ):4x+3y-7z+1=0\)
Phương trình tham số của d là:
(A) \(\left\{\begin{matrix} x=-1+4t\\ y=-2+3t\\ z=-3-7t \end{matrix}\right.\)
(B) \(\left\{\begin{matrix} x=1+4t\\ y=2+3t\\ z=3-7t \end{matrix}\right.\)
(C) \(\left\{\begin{matrix} x=1+3t\\ y=2-4t\\ z=3-7t \end{matrix}\right.\)
(D) \(\left\{\begin{matrix} x=-1+8t\\ y=-2+6t\\ z=-3-14t \end{matrix}\right.\)
-
Bài tập 13 trang 96 SGK Hình học 12
Cho hai đường thẳng: \(d_1:\left\{\begin{matrix} x=1+2t\\ y=2+3t\\ z=3+4t \end{matrix}\right.\) và \(d_2:\left\{\begin{matrix} x=3+4t'\\ y=5+6t'\\ z=7+8t' \end{matrix}\right.\)
Trong các mệnh đề sau, mệnh đề nào đúng?
(A) \(d_1\perp d_2\)
(B) \(d_1 // d_2\)
(C) \(d_1 \equiv d_2\)
(D) \(d_1\) và \(d_2\) chéo nhau.
-
Bài tập 14 trang 97 SGK Hình học 12
Cho mặt phẳng \((\alpha ): 2x+y+3z+1=0\) và đường thẳng d có phương trình tham số: \(\left\{\begin{matrix} x=-3+t\\ y=2-2t\\ z=1 \end{matrix}\right.\). Trong các mệnh đề sau, mệnh đề nào đúng?
(A) \(d\perp (\alpha )\)
(B) \(d\) cắt \((\alpha )\)
(C) \(d\) // \((\alpha )\)
(D) \(d \subset (\alpha )\)
-
Bài tập 15 trang 97 SGK Hình học 12
Cho (S) là mặt cầu tâm I(2;1;-1) và tiếp tục với mặt phẳng \((\alpha)\) có phương trình: \(2x-2y-z+3=0\).
Bán kính của (S) là:
(A) 2
(B) \(\frac{2}{3}\)
(C) \(\frac{4}{3}\)
(D) \(\frac{2}{9}\)
-
Bài tập 3.46 trang 131 SBT Hình học 12
Lập phương trình mặt phẳng (P) đi qua điểm M(1; -3; 2) và vuông góc với đường thẳng d: \(\frac{{x - 3}}{2} = \frac{{y + 1}}{{ - 1}} = \frac{z}{3}\)
-
Bài tập 3.47 trang 131 SBT Hình học 12
Lập phương trình mặt phẳng (P) đi qua điểm M(1; -3; 2) và song song với mặt phẳng (Q): x – z = 0.
-
Bài tập 3.48 trang 131 SBT Hình học 12
Lập phương trình mặt phẳng (P) đi qua ba điểm A(-1; -3; 2), B(-2; 1; 1) và C(0; 1; -1).
-
Bài tập 3.49 trang 132 SBT Hình học 12
Lập phương trình mặt phẳng (P) chứa hai đường thẳng:
\(d:\left\{ \begin{array}{l}
x = - 2 - t\\
y = 1 + 4t\\
z = 1 - t
\end{array} \right.\) và \(d':\left\{ {\begin{array}{*{20}{c}}
{x = - 1 + t'}\\
{y = - 3 + 4t'}\\
{z = 2 - 3t'}
\end{array}} \right.\) -
Bài tập 3.50 trang 132 SBT Hình học 12
Lập phương trình mặt phẳng (P) đi qua điểm I(-1; -1; 1) và chứa đường thẳng d: \(\frac{{x + 2}}{{ - 1}} = \frac{{y - 1}}{4} = \frac{{z - 1}}{{ - 1}}\)
-
Bài tập 3.51 trang 132 SBT Hình học 12
Lập phương trình mặt phẳng (P) chứa đường thẳng d: \(\left\{ {\begin{array}{*{20}{c}}
{x = - 2 - t}\\
{y = 1 + 4t}\\
{z = 1 - t}
\end{array}} \right.\) và song song với d1: \(\frac{{x - 1}}{1} = \frac{{y - 1}}{4} = \frac{{z - 1}}{{ - 3}}\) -
Bài tập 3.52 trang 132 SBT Hình học 12
Lập phương trình mặt phẳng (P) song song và cách đều hai mặt phẳng
(P1): 2x + y + 2z +1 = 0 và (P2): 2x + y + 2z +5 = 0.
-
Bài tập 3.53 trang 132 SBT Hình học 12
Cho hai mặt phẳng:
(P1): 2x + y + 2z +1 = 0 và (P2): 4x – 2y – 4z + 7 = 0.
Lập phương trình mặt phẳng sao cho khoảng cách từ mỗi điểm của nó đến (P1) và (P2) là bằng nhau.
-
Bài tập 3.54 trang 132 SBT Hình học 12
Cho hai đường thẳng d: \(\left\{ {\begin{array}{*{20}{c}}
{x = 6}\\
{y = - 2t}\\
{z = 7 + t}
\end{array}} \right.\) và d1: \(\left\{ {\begin{array}{*{20}{c}}
{x = - 2 + t'}\\
{y = - 2}\\
{z = - 11 - t'}
\end{array}} \right.\)Lập phương trình mặt phẳng (P) sao cho khoảng cách từ d và d1 đến (P) là bằng nhau.
-
Bài tập 3.56 trang 132 SBT Hình học 12
Lập phương trình tham số của đường thẳng d đi qua hai điểm phân biệt M0(x0 ;y0; z0) và M1(x1, y1, z1).
-
Bài tập 3.57 trang 132 SBT Hình học 12
Lập phương trình tham số của đường thẳng d đi qua điểm M0(x0, y0, z0) và vuông góc với mặt phẳng (P): Ax + By + Cz + D = 0.
-
Bài tập 3.58 trang 132 SBT Hình học 12
Lập phương trình tham số của đường thẳng d đi qua điểm M0(x0, y0, z0) và song song với hai mặt phẳng cắt nhau (P) Ax + By + Cz + D = 0 và (Q): A’x + B’y + C’z + D’ = 0
-
Bài tập 3.59 trang 133 SBT Toán 12
Cho mặt phẳng (P) : x + 2y – 2z + 3 = 0 và đường thẳng d: \(\left\{ {\begin{array}{*{20}{c}}
{x = 1 + t}\\
{y = 1 + t}\\
{z = 9}
\end{array}} \right.\)Lập phương trình đường thẳng d’ là hình chiếu vuông góc của d lên mặt phẳng (P).
-
Bài tập 3.60 trang 133 SBT Toán 12
Trong không gian Oxyz, cho điểm A(-4; -2; 4) và đường thẳng d: \(\left\{ {\begin{array}{*{20}{c}}
{x = - 3 + 2t}\\
{y = 1 - t}\\
{z = - 1 + 4t}
\end{array}} \right.\)Viết phương trình đường thẳng Δ đi qua A , cắt và vuông góc với đường thẳng d.
-
Bài tập 3.61 trang 133 SBT Toán 12
Trong không gian Oxyz, cho hai điểm A(2; 0; 0), B(0; 0; 8) và điểm C sao cho \(\overrightarrow {AC} = (0;6;0)\). Tính khoảng cách từ trung điểm I của BC đến đường thẳng OA.
-
Bài tập 3.62 trang 133 SBT Toán 12
Cho hình lập phương ABCD.A1B1C1D1 có cạnh bằng 1. Gọi M, N, P lần lượt là trung điểm của các cạnh BB1, CD, A1D1. Tính khoảng cách và góc giữa hai đường thẳng MP và C1N.
-
Bài tập 3.63 trang 133 SBT Toán 12
Trong không gian Oxyz, cho ba điểm A(1; 0; 0), B(1; 1; 1), \(C\left( {\frac{1}{3};\frac{1}{3};\frac{1}{3}} \right)\)
a) Viết phương trình tổng quát của mặt phẳng (α) đi qua O và vuông góc với OC.
b) Viết phương trình mặt phẳng (β) chứa AB và vuông góc với (α).
-
Bài tập 3.64 trang 133 SBT Toán 12
Trong không gian Oxyz, cho hai mặt phẳng (β) : x + 3ky – z + 2 = 0 và (γ) : kx – y + z + 1 = 0
Tìm k để giao tuyến của (β) và (γ) vuông góc với mặt phẳng \((\alpha ):x--y--2z + 5 = 0.\)
-
Bài tập 3.65 trang 133 SBT Toán 12
Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A’B’C’D’ có A(0; 0; 0), B(a; 0; 0), D(0; a; 0), A’(0; 0; b) với a > 0 và b> 0. Gọi M là trung điểm cạnh CC’.
Xác định tỉ số \(\frac{a}{b}\) để hai mặt phẳng (A’BD) và (MBD) vuông góc với nhau.
-
Bài tập 3.66 trang 134 SBT Toán 12
Cho hình chóp S.ABCD có đáy là hình thoi ABCD, AC cắt BD tại gốc tọa độ O. Biết A(2; 0; 0), B(0; 1; 0), \(S(0;0;2\sqrt 2 )\). Gọi M là trung điểm cạnh SC.
a) Viết phương trình mặt phẳng chứa SA và song song với BM.
b) Tính khoảng cách giữa hai đường thẳng SA và BM.
-
Bài tập 3.67 trang 134 SBT Toán 12
Cho mặt phẳng (P): 2x – 3y + 4z – 5 = 0 và mặt cầu (S):
x2 + y2 + z2 + 3x + 4y – 5z + 6 = 0
a) Xác định tọa độ tâm I và bán kính r của mặt cầu (S).
b) Tính khoảng cách từ tâm I đến mặt phẳng (P). Từ đó chứng minh rằng mặt phẳng (P) cắt mặt cầu (S) theo một đường tròn mà ta kí hiệu là (C). Xác định bán kính r’ và tâm H của đường tròn (C).
-
Bài tập 3.68 trang 134 SBT Toán 12
Trong không gian Oxyz, cho bốn điểm A(6; -2; 3), B(0; 1; 6), C(2; 0 ; -1), D(4; 1; 0). Gọi (S) là mặt cầu đi qua bốn điểm A, B, C, D. Hãy viết phương trình mặt phẳng tiếp xúc với mặt cầu (S) tại điểm A.
-
Bài tập 3.69 trang 134 SBT Toán 12
Trong không gian Oxyz, cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1) và D(1; 1; 0).
a) Viết phương trình mặt cầu (S) đi qua bốn điểm A, B, C, D.
b) Xác định tọa độ tâm và bán kính của đường tròn là giao tuyến của mặt cầu (S) với mặt phẳng (ACD).
-
Bài tập 3.70 trang 134 SBT Toán 12
Cho hai đường thẳng \({{\rm{\Delta }}_1}:\frac{x}{2} = \frac{{y + 2}}{3} = \frac{z}{4}\) và \({{\rm{\Delta }}_2}:\left\{ {\begin{array}{*{20}{c}}
{x = 1 + t}\\
{y = 2 + t}\\
{z = 1 + 2t}
\end{array}} \right.\)a) Viết phương trình mặt phẳng (α) chứa Δ1 và song song với Δ2
b) Cho điểm M(2; 1; 4). Tìm tọa độ điểm H thuộc đường thẳng Δ2 sao cho đoạn thẳng MH có độ dài nhỏ nhất.
-
Bài tập 3.71 trang 134 SBT Toán 12
Trong không gian Oxyz, cho điểm D(-3; 1 ; 2) và mặt phẳng (α) đi qua ba điểm A(1; 0; 11), B(0; 1; 10), C(1; 1; 8).
a) Viết phương trình đường thẳng AC.
b) Viết phương trình tổng quát của mặt phẳng (α).
c) Viết phương trình mặt cầu (S) tâm D, bán kính r = 5. Chứng minh mặt phẳng (α) cắt mặt cầu (S).
-
Bài tập 1 trang 114 SGK Hình học 12 NC
Cho ba điểm M(2; 0; 0), N(0; - 3; 0), P(0; 0; 4). Nếu MNPQ là một hình bình hành thì tọa độ điểm Q là:
(A) (-2; -3; 4)
(B) (3; 4; 2)
(C) (2; 3; 4)
(D) (-2; -3; -4)
-
Bài tập 2 trang 114 SGK Hình học 12 NC
Cho ba điểm A(1;2;0),B(1;0;−1),C(0;−1;2). Tam giác ABC là:
(A) Tam giác cân đỉnh A;
(B) Tam giác vuông đỉnh A;
(C) Tam giác đều;
(D) Không phải như (A), (B), (C).
-
Bài tập 3 trang 114 SGK Hình học 12 NC
Cho tam giác ABC có A(1;0;1), B(0;2;3), C(2;1;0). Độ dài đường cao tam giác kẻ từ C là:
(A) \(\sqrt {26} \)
(B) \(\frac{{\sqrt {26} }}{2}\)
(C) \(\frac{{\sqrt {26} }}{3}\)
(D) 26
-
Bài tập 4 trang 114 SGK Hình học 12 NC
Ba đỉnh của một hình bình hành có tọa độ là (1;1;1); (2;3;4); (6;5;2). Diện tích hình bình hành đó bằng:
(A) \(2\sqrt {83} \)
(B) \(\sqrt {83} \)
(C) 83
(D) \(\frac{{\sqrt {83} }}{2}\)
-
Bài tập 5 trang 114 SGK Hình học 12 NC
Cho A(1;0;0); B(0;1;0); C(0;0;1) và D(−2;1;−1). Thể tích của tứ diện ABCD là:
(A) 1
(B) 2
(C) \(\frac{1}{3}\)
(D) \(\frac{1}{2}\)
-
Bài tập 6 trang 114 SGK Hình học 12 NC
Cho A(−1;−2;4); B(−4;−2;0); C(3;−2;1) và D(1;1;1). Độ dài đường cao của tứ diện ABCD kẻ từ đỉnh D là:
(A) 3
(B) 1
(C) 2
(D)
-
Bài tập 7 trang 114 SGK Hình học 12 NC
Cho bốn điểm A(1;1;1), B(1;2;1), C(1;1;2) và D(2;2;1). Tâm I mặt cầu ngoại tiếp tứ diện ABCD là:
(A) \(\left( {\frac{3}{2}, - \frac{3}{2},\frac{3}{2}} \right)\)
(B) \(\left( {\frac{3}{2},\frac{3}{2},\frac{3}{2}} \right)\)
(C) \(\left( {3;3;3} \right)\)
(D) \(\left( {3; - 3;3} \right).\)
-
Bài tập 8 trang 115 SGK Hình học 12 NC
Bán kính mặt cầu tâm I(3;3;-4) tiếp xúc với trục Oy bằng:
(A) 5
(B) 4
(C) \(\sqrt 5 \)
(D) \(\frac{5}{2}.\)
-
Bài tập 9 trang 115 SGK Hình học 12 NC
Mặt cầu tâm I(2;1;−1) tiếp xúc với mặt phẳng tọa độ (Oyz) có phương trình là:
(A) \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 1} \right)^2} = 4;\)
(B) \({\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 1} \right)^2} = 1;\)
(C) \({\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} + {\left( {z - 1} \right)^2} = 4;\)
(D) \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z + 1} \right)^2} = 2.\)
-
Bài tập 10 trang 115 SGK Hình học 12 NC
Cho ba điểm A(1;1;3), B(−1;3;2) và C(−1;2;3). Mặt phẳng (ABC) có phương trình là:
(A) \(x + 2y + 2z - 3 = 0\)
(B) \(x - 2y + 3z - 3 = 0\)
(C) \(x + 2y + 2z - 9 = 0\)
(D) \({x^2} + 2y + 2z + 9 = 0\)
-
Bài tập 11 trang 115 SGK Hình học 12 NC
Cho ba điểm \(A\left( {1;0;0} \right),\,\,B\left( {0;2;0} \right),\,\,C\left( {0;0;3} \right).\) Phương trình nào sau đây không phải là phương trình mặt phẳng (ABC)?
(A) \(x + {y \over 2} + {z \over 3} = 1;\)
(B) \(6x + 3y + 2z - 6 = 0;\)
(C) \(6x + 3y + 2z + 6 = 0;\)
(D) \(12x + 6y + 4z - 12 = 0.\)
-
Bài tập 12 trang 116 SGK Hình học 12 NC
Cho hai điểm \(A\left( {1;3; - 4} \right)\) và \(B\left( { - 1;2;2} \right)\). Phương trình mặt phẳng trung trực của đoạn AB là:
(A) \(4x + 2y - 12z - 17 = 0;\)
(B) \(4x + 2y + 12z - 17 = 0;\)
(C) \(4x - 2y - 12z - 17 = 0;\)
(D) \(4x - 2y + 12z + 17 = 0.\)
-
Bài tập 13 trang 116 SGK Hình học 12 NC
Cho A(a; 0; 0), B(0; b; 0), C(0; 0; c), a, b, c là những số dương thay đổi sao cho \(\frac{1}{a} + \frac{1}{b} + \frac{1}{c} = 2\) Mặt phẳng (ABC) luôn đi qua một điểm cố định có tọa độ là:
(A) (1; 1; 1)
(B) (2; 2; 2)
(C) \(\left( {\frac{1}{2},\frac{1}{2},\frac{1}{2}} \right)\)
(D) \(\left( { - \frac{1}{2}, - \frac{1}{2}, - \frac{1}{2}} \right)\)
-
Bài tập 14 trang 116 SGK Hình học 12 NC
Cho điểm A(−1;2;1) và hai mặt phẳng (P): 2x+4y−6z−5 = 0 và (Q) : x+2y−3z = 0. Mệnh đề nào sau đây là đúng?
(A) Mp(Q) qua A và song song với (P);
(B) Mp(Q) không qua A và song song với (P);
(C) Mp(Q) qua A và không song song với (P);
(D) Mp(Q) không qua A và không song song với (P).
-
Bài tập 15 trang 116 SGK Hình học 12 NC
Cho điểm A(1;2;−5). Gọi M, N, P là hình chiếu của A lên ba trục Ox, Oy, Oz. Phương trình mặt phẳng (MNP) là:
(A) \(x + \frac{y}{2} - \frac{z}{5} = 1;\)
(B) \(x + \frac{y}{2} + \frac{z}{5} = 1;\)
(C) \(x + \frac{y}{2} - \frac{z}{5} = 0;\)
(D) \(x + \frac{y}{2} - \frac{z}{5} + 1 = 0.\)
-
Bài tập 16 trang 116 SGK Hình học 12 NC
Cho mặt cầu \(\left( S \right):{x^2} + {y^2} + {z^2} - 2\left( {x + y + z} \right) - 22 = 0\) và mặt phẳng \(3x - 2y + 6z + 14 = 0\) Khoảng cách từ tâm I của mặt cầu (S) tới mặt phẳng (P) là:
(A 1
(B) 2
(C) 3
(D) 4.
-
Bài tập 17 trang 117 SGK Hình học 12 NC
Mặt phẳng (P) cắt ba trục Ox, Oy, Oz tại A, B, C, trọng tâm tam giác ABC là G(−1;−3;2). Phương trình mặt phẳng (P) là:
(A) \(x + y - z - 5 = 0;\)
(B) \(2x - 3y - z - 1 = 0;\)
(C) \(x + 3y - 2z + 1 = 0;\)
(D) \(6x + 2y - 3z + 18 = 0.\)
-
Bài tập 18 trang 117 SGK Hình học 12 NC
Cho hình lập phương ABCD.A’B’C’D’ cạnh bằng 1. Gọi M là trung điểm cạnh BC. Tính khoảng cách từ A tới mặt phẳng (A’MD).
Một học sinh làm như sau:
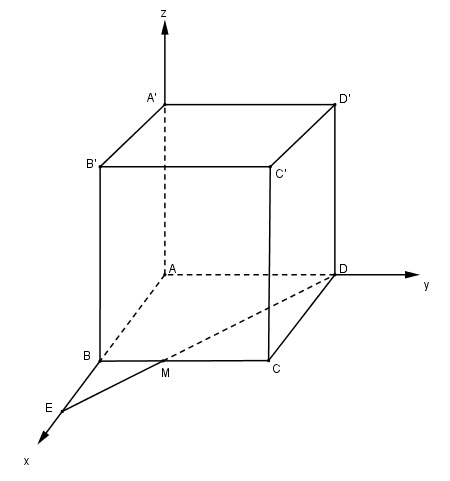
Bước 1: Chọn hệ trục tọa độ như hình vẽ. Kéo dài DM cắt AB tại E. Khi đó
A(0;0;0), E(2;0;0), D(0;1;0), A′(0;0;1)
Bước 2. Viết phương trình mặt phẳng (A’MD):
\(\frac{x}{2} + \frac{y}{1} + \frac{z}{1} = 1 \Leftrightarrow x + 2y + 2z - 2 = 0.\)
Bước 3. Khoảng cách
\(d\left( {A;\left( {A'MD} \right)} \right) = \frac{{\left| { - 2} \right|}}{{\sqrt {1 + 4 + 4} }} = \frac{2}{3}.\)
Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào?
(A) Đúng
(B) Sai ở bước 1
(C) Sai ở bước 2
(D) Sai ở bước 3.
-
Bài tập 19 trang 117 SGK Hình học 12 NC
Cho hai điểm A(1;−1;5) và B(0;0;1). Mặt phẳng (P) chứa A, B và song song với Oy có phương trình là:
(A) 4x−z+1 = 0
(B) 4x+y−z+1 = 0
(C) 2x+z−5 = 0
(D) y+4z−1 = 0
-
Bài tập 20 trang 118 SGK Hình học 12 NC
Mặt phẳng (P) chứa trục Oz và điểm A(2;−3;5) có phương trình là:
(A) 2x+3y = 0
(B) 2x−3y = 0
(C) 3x+2y = 0
(D) 3x−2y+z = 0
-
Bài tập 21 trang 118 SGK Hình học 12 NC
Cho mặt phẳng (P) có phương trình x−y−1 = 0. Điểm H(2;−1;−2) là hình chiếu vuông góc của gốc tọa độ O trên một mặt phẳng (Q). Góc giữa hai mặt phẳng (P) và (Q) là:
(A) 300
(B) 450
(C) 600
(D) 900
-
Bài tập 22 trang 118 SGK Hình học 12 NC
Cho điểm A(1; 2; 3) và đường thẳng \(d:\frac{x}{3} = \frac{{y - 1}}{4} = z + 3\). Phương trình mặt phẳng (A,d) là:
(A) 23x+17y−z+14 = 0
(B) 23x−17y−z+14 = 0
(C) 23x+17y+z−60 = 0
(D) 23x−17y+z−14 = 0
-
Bài tập 23 trang 118 SGK Hình học 12 NC
Cho hai đường thẳng
\({d_1}:\frac{{x - 1}}{1} = \frac{y}{2} = \frac{{z - 3}}{3};\,{d_2}:\left\{ {\begin{array}{*{20}{c}}
{x = 2t}\\
{y = 1 + 4t}\\
{z = 2 + 6t.}
\end{array}} \right.\)Khẳng định nào sau đây là đúng?
(A) d1, d2 cắt nhau
(B) d1, d2 trùng nhau
(C) d1 // d2
(D) d1, d2 chéo nhau.
-
Bài tập 24 trang 118 SGK Hình học 12 NC
Cho mặt phẳng \(\left( \alpha \right):x + 3y + z + 1 = 0\) và đường thẳng
\(d:\left\{ {\begin{array}{*{20}{c}}
{x = 1 + t}\\
{y = 2 - t}\\
{z = 2 - 3t}
\end{array}} \right.\)Tọa độ giao điểm A của d và \(\left( \alpha \right)\) là:
(A) A(3; 0; 4)
(B) A(3;−4;0)
(C) A(−3;0;4)
(D) A(3;0;−4)
-
Bài tập 25 trang 119 SGK Hình học 12 NC
Cho đường thẳng
\(d:\left\{ {\begin{array}{*{20}{c}}
{x = 2t}\\
{y = 1 - t}\\
{z = 2 + t.}
\end{array}} \right.\)Phương trình nào sau đây cũng là phương trình của đường thẳng d?
(A) \(\left\{ {\begin{array}{*{20}{c}}
{x = 2 - 2t}\\
{y = - t}\\
{z = 3 + t}
\end{array}} \right.\)(B) \(\left\{ {\begin{array}{*{20}{c}}
{x = 4 - 2t}\\
{y = - 1 + t}\\
{z = 4 - t}
\end{array}} \right.\)(C) \(\left\{ {\begin{array}{*{20}{c}}
{x = 4 + 2t}\\
{y = 1 - t}\\
{z = 4 + t}
\end{array}} \right.\)(D) \(\left\{ {\begin{array}{*{20}{c}}
{x = 2t}\\
{y = 1 + t}\\
{z = 2 + t}
\end{array}} \right.\) -
Bài tập 26 trang 119 SGK Hình học 12 NC
Cho hai điểm A(2;3;−1), B(1;2;4) và ba phương trình sau:
\(\begin{array}{l}
\left( I \right)\left\{ \begin{array}{l}
x = 2 - t\\
y = 3 - t\\
z = - 1 + 5t
\end{array} \right.\\
\left( {II} \right)\frac{{x - 2}}{1} = \frac{{y - 3}}{1} = \frac{{z + 1}}{{ - 5}}\\
\left( {III} \right)\left\{ \begin{array}{l}
x = 1 - t\\
y = 2 - t\\
z = 4 + 5t
\end{array} \right.
\end{array}\)Mệnh đề nào sau đây là đúng?
(A) Chỉ có (I) là phương trình của đường thẳng AB;
(B) Chỉ có (III) là phương trình của đường thẳng AB;
(C) Chỉ có (I) và (II) là phương trình của đường thẳng AB;
(D) Cả (I), (II) và (III) là phương trình của đường thẳng AB.
-
Bài tập 27 trang 119 SGK Hình học 12 NC
Cho ba điểm A(1; 3; 2), B(1; 2; 1), C(1; 1; 3). Viết phương trình đường thẳng Δ đi qua trọng tâm G của tam giác ABC và vuông góc với mp(ABC).
Một học sinh làm như sau:
Bước 1: Tọa độ trong tâm G của tam giác ABC là
\(\left\{ {\begin{array}{*{20}{c}}
{{x_G} = \frac{{1 + 1 + 1}}{3} = 1}\\
{{y_G} = \frac{{3 + 2 + 1}}{3} = 2}\\
{{z_G} = \frac{{2 + 1 + 3}}{3} = 2.}
\end{array}} \right.\)Bước 2: Vectơ pháp tuyến của mp(ABC) là
\(\vec n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( { - 3;1;0} \right).\)
Bước 3: Phương trình tham số của đường thẳng Δ là:
\(\left\{ \begin{array}{l}
x = 1 - 3t\\
y = 2 + t\\
z = 2
\end{array} \right.\)Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào?
(A) Đúng
(B) Sai ở bước 1
(C) Sai ở bước 2
(D) Sai ở bước 3.
-
Bài tập 28 trang 120 SGK Hình học 12 NC
Gọi d là đường thẳng đi qua gốc tọa độ O, vuông góc với trục Ox và vuông góc với đường thẳng
\({\rm{\Delta }}:\left\{ {\begin{array}{*{20}{c}}
{x = 1 + t}\\
{y = 2 - t}\\
{z = 1 - 3t.}
\end{array}} \right.\)Phương trình của d là:
(A) \(\left\{ {\begin{array}{*{20}{c}}
{x = t}\\
{y = 3t}\\
{z = - t}
\end{array}} \right.\)(B) \(\left\{ {\begin{array}{*{20}{c}}
{x = 1}\\
{y = - 3t}\\
{z = - t}
\end{array}} \right.\)(C) \(\frac{x}{1} = \frac{y}{3} = \frac{z}{{ - 1}}\)
(D) \(\left\{ {\begin{array}{*{20}{c}}
{x = 0}\\
{y = - 3t}\\
{z = t}
\end{array}} \right.\) -
Bài tập 29 trang 120 SGK Hình học 12 NC
Cho đường thẳng
\(d:\left\{ {\begin{array}{*{20}{c}}
{x = 3 + 4t}\\
{y = - 1 - t}\\
{z = 4 + 2t}
\end{array}} \right.\)Và mặt phẳng \(\left( P \right):x + 2y - z + 3 = 0\)
Trong các mệnh đề sau đây, mệnh đề nào đúng?
(A) d song song với (P)
(B) d cắt (P)
(C) d vuông góc với (P)
(D) d nằm trên (P)
-
Bài tập 30 trang 121 SGK Hình học 12 NC
Cho điểm A(1; 1; 1) và đường thẳng
\(d:\left\{ \matrix{
x = 6 - 4t \hfill \cr
y = - 2 - t \hfill \cr
z = - 1 + 2t\,. \hfill \cr} \right.\)Hình chiếu của A trên d có tọa độ là
(A) \(\left( {2; - 3;1} \right);\) (B) \(\left( {2; - 3; - 1} \right);\)
(C) \((2; 3; 1)\); (D) \(\left( { - 2;3;1} \right).\)
-
Bài tập 31 trang 121 SGK Hình học 12 NC
Cho tứ diện ABCD có A(1; 0; 0), B(1; 1; 0), C(0; 1; 0) và D(0; 0; 2).
Tính khoảng cách giữa hai đường thẳng AC và BD.
Một học sinh làm như sau:
Bước 1:
\(\begin{array}{l}
\overrightarrow {AC} = \left( { - 1;1;0} \right)\\
\overrightarrow {BD} = \left( { - 1; - 1;2} \right),\overrightarrow {AB} = \left( {0;1;0} \right).
\end{array}\)Bước 2: \(\left[ {\overrightarrow {AC} ,\overrightarrow {BD} } \right] = \left( {2;2;2} \right)\)
Bước 3:
\(\begin{array}{l}
d\left( {AC,BD} \right) = \frac{{\left| {\left[ {\overrightarrow {AC} ,\overrightarrow {BD} } \right].\overrightarrow {AB} } \right|}}{{\left| {\left[ {\overrightarrow {AC} ,\overrightarrow {BD} } \right]} \right|}}\\
= \frac{2}{{\sqrt {12} }} = \frac{{\sqrt 3 }}{3}.
\end{array}\)Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào?
(A) Đúng
(B) Sai ở bước 1
(C) Sai ở bước 2
(D) Sai ở bước 3
-
Bài tập 32 trang 121 SGK Hình học 12 NC
Cho \(\left| {\vec u} \right| = 2,\left| {\vec v} \right| = 1,\left( {\vec u,\vec v} \right) = \frac{\pi }{3}\)
Góc giữa vectơ \(\vec u\) và \(\vec u - \vec v\) bằng:
(A) 300
(B) 450
(C) 600
(D) 900
-
Bài tập 33 trang 121 SGK Hình học 12 NC
Cho \(\left| {\vec u} \right| = 2,\left| {\vec v} \right| = 5,\left( {\vec u,\vec v} \right) = \frac{\pi }{6}\) Độ dài vectơ \(\left[ {\vec u,\vec v} \right]\) bằng:
(A) 10
(B) 5
(C) 8
(D) \(5\sqrt 3 \)
-
Bài tập 34 trang 122 SGK Hình học 12 NC
Mặt phẳng \(2x - 3y + z - 1 = 0\) cắt các trục tọa độ tại các điểm:
(A) \(\left( {\frac{1}{2};0;0} \right),\left( {0; - \frac{1}{3};0} \right),\left( {0;0;1} \right)\)
(B) \(\left( {1;0;0} \right),\left( {0;\frac{1}{3};0} \right),\left( {0;0;1} \right)\)
(C) \(\left( {\frac{1}{2};0;0} \right),\left( {0;\frac{1}{3};0} \right),\left( {0;0;1} \right)\)
(D) \(\left( {\frac{1}{2};0;0} \right),\left( {0; - \frac{1}{3};0} \right),\left( {0;0; - 1} \right)\)
-
Bài tập 35 trang 122 SGK Hình học 12 NC
Cho đường thẳng
\(d:\left\{ {\begin{array}{*{20}{c}}
{x = - \frac{9}{5} - t}\\
{y = 5t}\\
{z = \frac{7}{5} + 3t}
\end{array}} \right.\)Và mặt phẳng \(\left( P \right):3x - 2y + 3z - 1 = 0\)
Gọi d’ là hình chiếu của d trên (P). Trong các vectơ sau, vectơ nào không phải là vectơ chỉ phương của d’ ?
(A) (5;−51;39)
(B) (10;−102;−78)
(C) (−5;51;39)
(D) (5;51;39)
-
Bài tập 36 trang 122 SGK Hình học 12 NC
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1. Gọi M, N, P lần lượt là trung điểm của A’B’, BC, DD’. Chứng minh rằng \(AC' \bot \left( {MNP} \right).\)
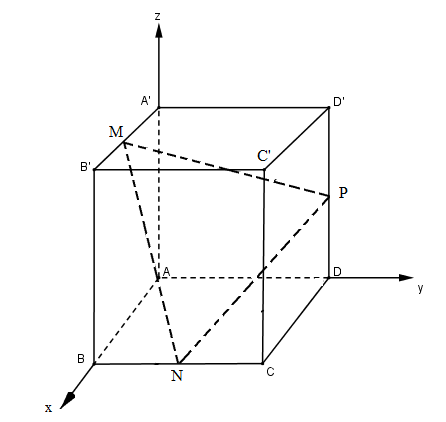
Một học sinh làm như sau:
Bước 1: Chọn hệ trục tọa độ như hình 71;
Khi đó A(0; 0; 0), C’(1; 1; 1),
\(M = \left( {\frac{1}{2};0;1} \right),N\left( {1;\frac{1}{2};0} \right),P\left( {0;1;\frac{1}{2}} \right).\)
Bước 2:
\(\begin{array}{l}
\overrightarrow {AC'} = \left( {1;1;1} \right),\overrightarrow {MN} = \left( {\frac{1}{2};\frac{1}{2}; - 1} \right)\\
\overrightarrow {MP} = \left( { - \frac{1}{2};1; - \frac{1}{2}} \right).
\end{array}\)Bước 3:
\(\left\{ \begin{array}{l}
\overrightarrow {AC\prime } .\overrightarrow {MN} = 0\\
\overrightarrow {AC\prime } .\overrightarrow {MP} = 0
\end{array} \right. \Rightarrow AC\prime \bot (MNP).\)Bài giải trên đúng hay sai? Nếu sai thì sai ở bước nào?
(A) Đúng
(B) Sai ở bước 1
(C) Sai ở bước 2
(D) Sai ở bước 3
-
Bài tập 37 trang 123 SGK Hình học 12 NC
Cho đường thẳng
\(d:\left\{ {\begin{array}{*{20}{c}}
{x = 0}\\
{y = t}\\
{z = 2 - t}
\end{array}} \right.\)Phương trình đường vuông góc chung của d và trục Ox là:
(A) \(\left\{ {\begin{array}{*{20}{c}}
{x = 1}\\
{y = t}\\
{z = t}
\end{array}} \right.\)(B) \(\left\{ {\begin{array}{*{20}{c}}
{x = 0}\\
{y = 2t}\\
{z = t}
\end{array}} \right.\)(C) \(\left\{ {\begin{array}{*{20}{c}}
{x = 0}\\
{y = 2 - t}\\
{z = t}
\end{array}} \right.\)(D) \(\left\{ {\begin{array}{*{20}{c}}
{x = 0}\\
{y = t}\\
{z = t}
\end{array}} \right.\) -
Bài tập 38 trang 123 SGK Hình học 12 NC
Cho mặt phẳng (P) : x−2y−3z+14 = 0 và điểm M(1;−1;1). Tọa độ của điểm M’ đối xứng với M qua mp(P) là
(A) (−1;3;7)
(B) (1;−3;7)
(C) (2;−3;−2)
(D) (2;−1;1).
-
Bài tập 39 trang 123 SGK Hình học 12 NC
Cho điểm A(0;−1;3) và đường thẳng
\(d:\left\{ {\begin{array}{*{20}{c}}
{x = 1 + 2t}\\
{y = 2}\\
{z = - t}
\end{array}} \right.\)Khoảng cách từ A đến d bằng:
(A) \(\sqrt 3 \)
(B) \(\sqrt {14} \)
(C) \(\sqrt 6 \)
(D) \(\sqrt 8 \)
-
Bài tập 40 trang 124 SGK Hình học 12 NC
Cho điểm M(−1;2;−3). Gọi M1, M2, M3 lần lượt là điểm đối xứng của M qua các mặt phẳng (Oxy), (Oxz), (Oyz). Phương trình mp(M1M2M3) là:
(A) 6x+2y+3z+6 = 0
(B) 6x−2y+3z+6 = 0
(C) 6x−3y+2z+6 = 0
(D) 6x−3y−2z+6 = 0
-
Bài tập 41 trang 124 SGK Hình học 12 NC
Cho mặt cầu \(\left( S \right):{\left( {x - 1} \right)^2} + {\left( {y + 3} \right)^2} + {\left( {z - 2} \right)^2} = 49\)
Phương trình nào sau đây là phương trình của mặt phẳng tiếp xúc với mặt cầu (S) ?
(A) 6x+2y+3z = 0
(B) 2x+3y+6z−5 = 0
(C) 6x+2y+3z−55 = 0
(D) x+2y+2z−7 = 0
-
Bài tập 42 trang 124 SGK Hình học 12 NC
Cho mặt cầu \({x^2} + {y^2} + {z^2} - 2x - 4y - 6z = 0\)
Trong ba điểm (0; 0; 0); (1; 2; 3), (2; -1; -1), có bao nhiêu điểm nằm trong mặt cầu (S) ?
(A) 0
(B) 1
(C) 2
(D) 3.






