Bài tập 1 trang 62 SGK Hình học 10

Định nghĩa: Với mỗi góc  \(\alpha \) \(\left( {{0^0} \le \alpha  \le {{180}^0}} \right)\) ta xác định một điểm \(M\) trên nửa đường tròn đơn vị sao cho góc \(\widehat {xOM} = \alpha \) và giả sử điểm \(M\) có tọa độ \(M({x_0};{y_0})\). Khi đó ta có định nghĩa:

sin của góc \(\alpha \) là \({y_0}\), kí hiệu là \(\sin \alpha  = {y_0}\)

cosin của góc \(\alpha \) là \({x_0}\), kí hiệu là \(\cos \alpha  = {x_0}\)

tan của góc \(\alpha \) là \(\frac{{{y_0}}}{{{x_0}}}\)  \(({x_0} \ne 0)\), kí hiệu \(\tan \alpha  = \frac{{{y_0}}}{{{x_0}}}\)

cotan cuả góc \(a\) là \(\frac{{{x_0}}}{{{y_0}}}\)  \(({y_0} \ne 0)\), ký hiệu \(\cot \alpha  = \frac{{{x_0}}}{{{y_0}}}\)

Các số \(\sin \alpha ,\cos \alpha ,\tan \alpha ,\cot \alpha \) được gọi là các giá trị lượng giác của góc \(\alpha .\)

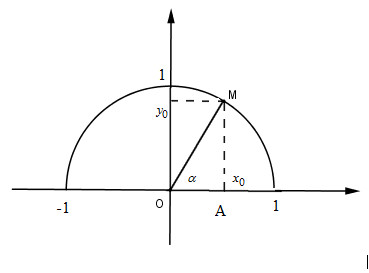
Khi \(a\) là các góc nhọn thì:

Theo định nghĩa ta có: \(\sin \alpha  = {y_0}\)

Trong tam giác OAM vuông tại \(A\), ta có: \(\sin \alpha  = \frac{{{y_0}}}{1} = {y_0}\)

Theo định nghĩa ta có: \(\cos \alpha  = {x_0}\)

Trong tam giác OAM vuông tại \(A\), ta có: \(\cos \alpha  = \frac{{OA}}{{OM}} = \frac{{{x_0}}}{1} = {x_0}\)

Theo định nghĩa ta có: \(\tan \alpha  = \frac{{{y_0}}}{{{x_0}}}({x_0} \ne 0)\)

Trong tam giác OAM vuông tại \(A\), ta có: \(\tan \alpha  = \frac{{AM}}{{OA}} = \frac{{{y_0}}}{{{x_0}}}\)

Theo định nghĩa ta có: \(\cot \alpha  = \frac{{{x_0}}}{{{y_0}}}({y_0} \ne 0)\)

Trong tam giác OAM vuông tại \(A\), ta có:  \(\cot \alpha  = \frac{{OA}}{{AM}} = \frac{{{x_0}}}{{{y_0}}}\)

-- Mod Toán 10 HỌC247