Bài tập 1.80 trang 40 SBT Toán 12

a) Với m = 1 ta được hàm số \(y = {x^4} - 2{x^2}\)

Có \(y' = 4{x^3} - 4x = 4x({x^2} - 1);\)

\(y' = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x =  - 1}\\
{x = 0}\\
{x = 1}
\end{array}} \right.\)

Bảng biến thiên:

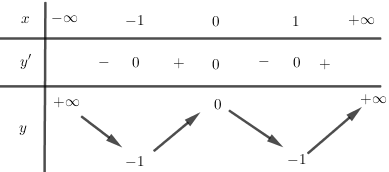
Đồ thị:

b) Để (C_m) tiếp xúc với trục hoành tại hai điểm phân biệt thì điều kiện cần và đủ là hàm số đã cho có hai điểm cực tiểu, 1 điểm cực đại và \({y_{CT}} = 0\).

Ta có: \(y' = 4{x^3} - 4mx = 4x\left( {{x^2} - m} \right);\)

\(y\prime  = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
{x^2} = m
\end{array} \right.\)

Để hàm số có hai điểm cực tiểu, một điểm cực đại thì phương trình x² = m có hai nghiệm phân biệt khác \(0 \Leftrightarrow m > 0 \Leftrightarrow m > 0\).

Khi đó hàm số có hai điểm cực tiểu là \(x = \sqrt m \) và \(x = -\sqrt m \);

\(\begin{array}{l}
 \Rightarrow {y_{CT}} = f\left( { \pm \sqrt m } \right)\\
 = {m^2} - 2{m^2} + {m^3} - {m^2} = {m^3} - 2{m^2}\\
{y_{CT}} = 0 \Leftrightarrow {m^3} - 2{m^2} = 0\\
 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{m = 0(KTM)}\\
{m = 2\left( {TM} \right)}
\end{array}} \right.
\end{array}\)

Vậy m = 2 là giá trị cần tìm.

-- Mod Toán 12 HỌC247