Bài tập 71 trang 62 SGK Toán 12 NC
Chu vi của một tam giác là 16cm, độ dài một cạnh tam giác là 6cm. Tìm độ dài hai cạnh còn lại của tam giác sao cho tam giác có diện tích lớn nhất.
Hướng dẫn: Có thể áp dụng công thức Hê-rông để tính diện tích tam giác: Nếu tam giác ABC có độ dài các cạnh là a, b, c thì diện tích của nó là: \(S = \sqrt {p(p - a)(p - b)(p - c)} \) (p là nửa chu vi của tam giác.)
Hướng dẫn giải chi tiết
Gọi x, y là độ dài hai cạnh còn lại của tam giác.
Ta có: x + y = 16 − 6 = 10, x > 0, y > 0
Diện tích tam giác
\(\begin{array}{*{20}{l}}
{S = \sqrt {p(p - a)(p - b)(p - c)} }\\
\begin{array}{l}
= \sqrt {8.2(8 - x)(8 - y)} \\
= 4\sqrt {(8 - x)(8 - y)}
\end{array}
\end{array}\)
Thay y = 10 - x, ta được:
\(\begin{array}{l}
S = 4\sqrt {(8 - x)(x - 2)} \\
= 4\sqrt { - {x^2} + 10x - 16} (0 < x < 10)
\end{array}\)
S đạt giá trị lớn nhất trên khoảng (0;10) khi và chỉ khi hàm số f(x) = −x2 + 10x − 16 đạt giá trị lớn nhất trên khoảng (0;10).
f′(x) = −2x + 10, f′(x) = 0 ⇔ x = 5, f(5) = 9
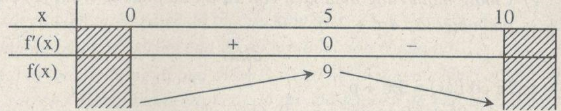
Tam giác có diện tích lớn nhất khi x = 5 (cm) và y= 5 (cm)
\(\mathop {max}\limits_{x \in (0;10)} f(x) = f(5) = 9\)
Khi đó diện tích tam giác là:
\(S = 4\sqrt 9 = 12(c{m^2})\)
-- Mod Toán 12 HỌC247
-

 Đang cần gấp
Đang cần gấp Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tính đạo hàm của hàm số y=(1-x)/2^x
bởi Trangg Anh
 16/12/2019
Tinh dao ham
16/12/2019
Tinh dao ham Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Giải phương trình 3tan^2 x+(6+căn 3)tanx+2 căn 3=0
bởi Phượng AnMi
 15/12/2019
15/12/2019
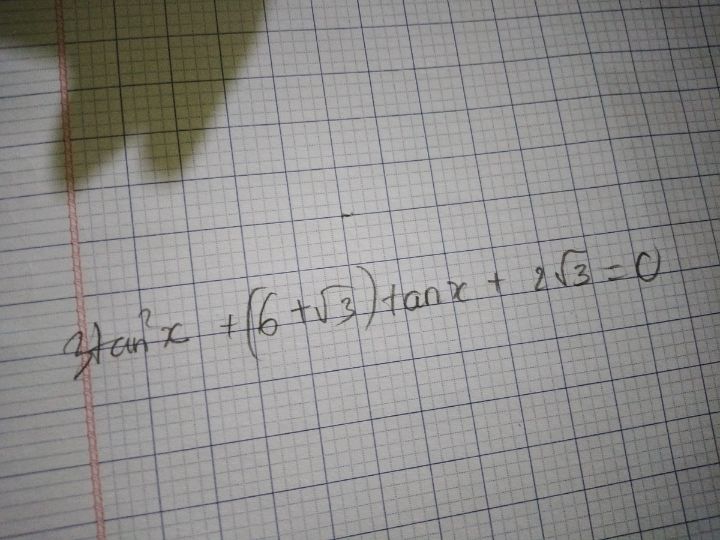 Theo dõi (0) 4 Trả lời
Theo dõi (0) 4 Trả lời -


Tính P = ab biết tiếp tuyến của (C) tại điểm M song song với đường thẳng d:y=2x−3
bởi Nguyễn Hữu Chí
 15/12/2019
Biết rằng đồ thị (C) của hàm số y=ax bx−1y=ax bx−1 cắt trục tung tại điểm M có tung độ bằng 1 và tiếp tuyến của (C) tại điểm M song song với đường thẳng d:y=2x−3d:y=2x−3. Tính P = ab.Theo dõi (0) 0 Trả lời
15/12/2019
Biết rằng đồ thị (C) của hàm số y=ax bx−1y=ax bx−1 cắt trục tung tại điểm M có tung độ bằng 1 và tiếp tuyến của (C) tại điểm M song song với đường thẳng d:y=2x−3d:y=2x−3. Tính P = ab.Theo dõi (0) 0 Trả lời -


Tổng các khoảng cách bé nhất từ điểm M thuộc (C) đến hai đường tiệm cận của đồ thị (C) là?
bởi Thịnh Trần
 13/12/2019
Câu 16 nha các bạn oie
13/12/2019
Câu 16 nha các bạn oie Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm m để đồ thị hàm số y=(x+2)/(x-1) cắt đường thẳng y=x+m tại 2 điểm phân biệt A, B
bởi Phạm Công Thiên Kym
 12/12/2019
Câu 7 ạ
12/12/2019
Câu 7 ạ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính tổng A tất cả các giá trị thực của tham số m để đồ thị hàm số y=x^4-2mx^2+1 có 3 điểm cực trị
bởi Liêu Nguyên Phan
 12/12/2019
12/12/2019
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm m nguyên để đồ thị hàm số y=(x-2)/(x^2-3mx+m) có đúng 1 tiệm cận đứng
bởi Tiên Võ Thị
 10/12/2019
.
10/12/2019
. Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời
Bài tập SGK khác
Bài tập 69 trang 61 SGK Toán 12 NC
Bài tập 70 trang 61 SGK Toán 12 NC
Bài tập 72 trang 62 SGK Toán 12 NC
Bài tập 73 trang 62 SGK Toán 12 NC
Bài tập 74 trang 62 SGK Toán 12 NC
Bài tập 75 trang 62 SGK Toán 12 NC
Bài tập 76 trang 62 SGK Toán 12 NC
Bài tập 77 trang 62 SGK Toán 12 NC
Bài tập 78 trang 62 SGK Toán 12 NC
Bài tập 79 trang 62 SGK Toán 12 NC
Bài tập 80 trang 64 SGK Toán 12 NC
Bài tập 81 trang 64 SGK Toán 12 NC
Bài tập 82 trang 64 SGK Toán 12 NC
Bài tập 83 trang 64 SGK Toán 12 NC
Bài tập 84 trang 65 SGK Toán 12 NC
Bài tập 85 trang 65 SGK Toán 12 NC
Bài tập 86 trang 65 SGK Toán 12 NC
Bài tập 87 trang 65 SGK Toán 12 NC
Bài tập 88 trang 65 SGK Toán 12 NC
Bài tập 89 trang 65 SGK Toán 12 NC
Bài tập 90 trang 65 SGK Toán 12 NC
Bài tập 91 trang 65 SGK Toán 12 NC
Bài tập 92 trang 66 SGK Toán 12 NC
Bài tập 93 trang 66 SGK Toán 12 NC
Bài tập 94 trang 66 SGK Toán 12 NC
Bài tập 95 trang 66 SGK Toán 12 NC
Bài tập 96 trang 66 SGK Toán 12 NC
Bài tập 97 trang 67 SGK Toán 12 NC
Bài tập 98 trang 67 SGK Toán 12 NC





