Bài tập 73 trang 62 SGK Toán 12 NC
Cho hàm số f(x) = x3 + px + q
a) Tìm điều kiện đối với p và q để hàm số f có một cực đại và một cực tiểu.
b) Chứng minh rằng nếu giá trị cực đại và giá trị cực tiểu trái dấu thì phương trình: x3 + px + q = 0 (1) có ba nghiệm phân biệt.
c) Chứng minh rằng điều kiện cần và đủ để phương trình (1) có ba nghiệm phân biệt là: 4p3 + 27q2 < 0
Hướng dẫn giải chi tiết
a) Ta có: \(f'\left( x \right) = 3{x^2} + p\)
\(f\prime (x) = 0 \Leftrightarrow 3{x^2} + p = 0(1)\)
Hàm số f có một cực đại và một cực tiểu khi và chỉ khi khi phương trình (1) có hai nghiệm phân biệt ⇔p < 0
Khi đó hai nghiệm của (1) là:
\(x = - \sqrt { - \frac{p}{3}} ; x = \sqrt { - \frac{p}{3}} \)
Bảng biến thiên
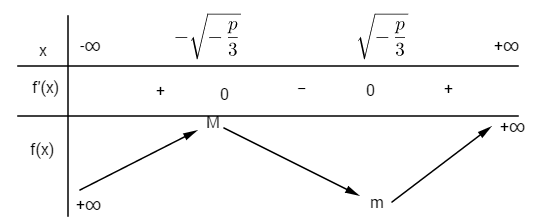
\(\begin{array}{l}
M = {\sqrt { - \left( { - \frac{p}{3}} \right)} ^3} - p\sqrt { - \frac{p}{3}} + q\\
= q - \frac{2}{3}p\sqrt { - \frac{p}{3}}
\end{array}\)
\(\begin{array}{l}
m = {\sqrt { - \left( { - \frac{p}{3}} \right)} ^3} + p\sqrt { - \frac{p}{3}} + q\\
= q + \frac{2}{3}p\sqrt { - \frac{p}{3}}
\end{array}\)
b) Nếu Mm < 0 và m < 0, khi đó, phương trình f(x) = 0 có ba nghiệm α, β, γ với
\(\alpha < - \sqrt { - \frac{p}{3}} ; - \sqrt { - \frac{p}{3}} < \beta < \sqrt { - \frac{p}{3}} \)
Và \(\gamma > \sqrt { - \frac{p}{3}} \)
c) Nếu Mm > 0 thì hai số M và m cùng dấu.
+ Nếu M < 0 và m < 0 thì phương trình (1) có nghiệm duy nhất (Lớn hơn \(\sqrt { - \frac{p}{3}} \))
+ Nếu M > 0 và m > 0 thì phương trình (1) có nghiệm duy nhất ( Nhỏ hơn \(\sqrt { - \frac{p}{3}} \))
Vậy điều kiện cần và đủ để phương trình (1) có ba nghiệm phân biệt là:
\(\begin{array}{l}
\left\{ {\begin{array}{*{20}{l}}
{p < 0}\\
{Mm = {q^2} - \frac{4}{9}{p^2}\left( { - \frac{p}{3}} \right) < 0}
\end{array}} \right.\\
\Leftrightarrow 4{p^3} + 27{q^2} < 0
\end{array}\)
-- Mod Toán 12 HỌC247
-

 tìm m để phương trình x^3 -3x = m^2 m có 3 nghiệm phân biệtTheo dõi (0) 7 Trả lời
tìm m để phương trình x^3 -3x = m^2 m có 3 nghiệm phân biệtTheo dõi (0) 7 Trả lời -


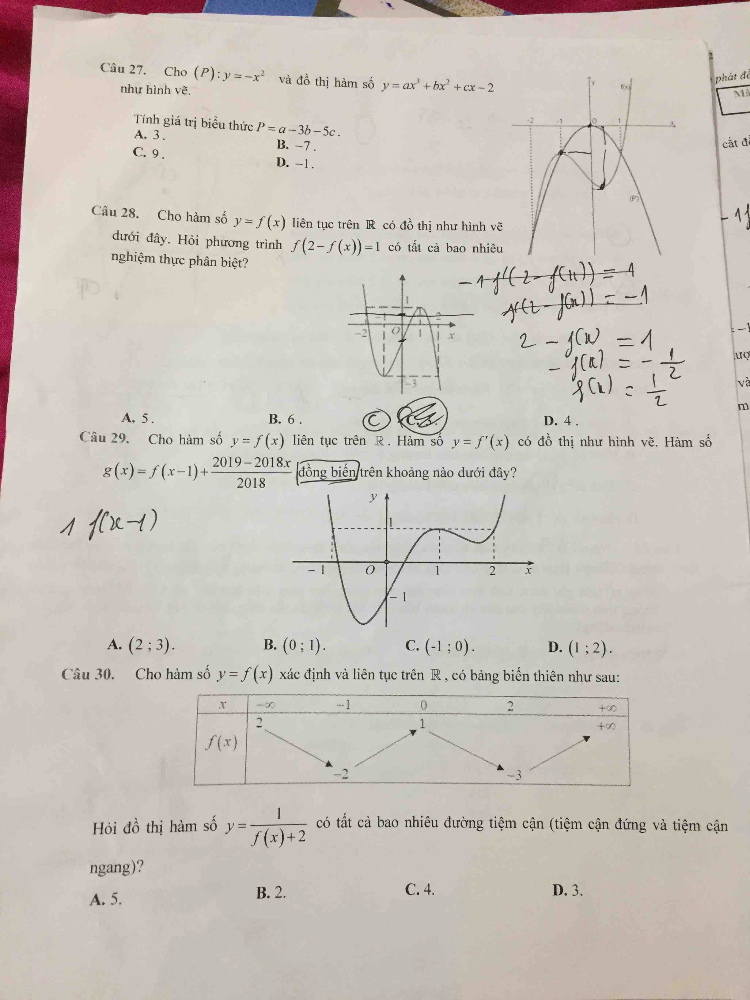
Đồ thị hàm số y=1/(f(x)+2) có bao nhiêu đường tiệm cận?
bởi Ngọc Thu
 17/10/2019
17/10/2019
 Theo dõi (0) 7 Trả lời
Theo dõi (0) 7 Trả lời -


Tìm m để đồ thị hàm số y=(x+2)/(x^2-4x+m) có 1 tiệm cận đứng và 1 tiệm cận ngang
bởi Dai Dang
 16/10/2019
Tính tổng tất cả giá trị của m
16/10/2019
Tính tổng tất cả giá trị của m Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -


Có bao nhiêu tiếp tuyến của đồ thị hàm số y=-x^3+2x^2 song song với đường thẳng y=x?
bởi Nguyễn Thùy Duyên
 16/10/2019
.
16/10/2019
. Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Tìm m để phương trình căn(x^2-4x+5)=m+4x-x^2 có đúng 2 nghiệm phân biệt
bởi Lường Thị Thanh Mai
 15/10/2019
15/10/2019
 Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -


Tìm m để hàm số y=2x^3-3(3m-1)x^2+6(2m^2-m)x+3 nghịch biến trên đoạn có độ dài bằng 4
bởi Thị Trang
 13/10/2019
Giải giúp mình câu 8 ạ:((
13/10/2019
Giải giúp mình câu 8 ạ:((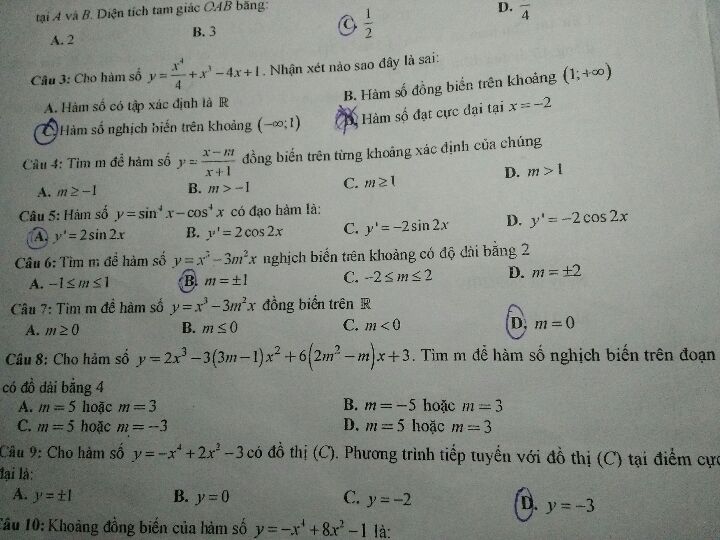 Theo dõi (0) 7 Trả lời
Theo dõi (0) 7 Trả lời -


Tìm m để đường thẳng d: y=x+m cắt đồ thị hàm số (C):y=(x-1)/(x+2) tại 2 điểm phân biệt
bởi Uyên Trần Uyên
 11/10/2019
Ai giải bài 14 giúp em với
11/10/2019
Ai giải bài 14 giúp em với Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -


Tìm m để đồ thị hàm số y=x^4-2mx^2+m^4+2m có 3 điểm cực trị tạo thành 1 tam giác trong đó có 1 góc bằng 120 độ
bởi Nguyễn Thu Hiền
 11/10/2019
11/10/2019
 Theo dõi (1) 6 Trả lời
Theo dõi (1) 6 Trả lời
Bài tập SGK khác
Bài tập 71 trang 62 SGK Toán 12 NC
Bài tập 72 trang 62 SGK Toán 12 NC
Bài tập 74 trang 62 SGK Toán 12 NC
Bài tập 75 trang 62 SGK Toán 12 NC
Bài tập 76 trang 62 SGK Toán 12 NC
Bài tập 77 trang 62 SGK Toán 12 NC
Bài tập 78 trang 62 SGK Toán 12 NC
Bài tập 79 trang 62 SGK Toán 12 NC
Bài tập 80 trang 64 SGK Toán 12 NC
Bài tập 81 trang 64 SGK Toán 12 NC
Bài tập 82 trang 64 SGK Toán 12 NC
Bài tập 83 trang 64 SGK Toán 12 NC
Bài tập 84 trang 65 SGK Toán 12 NC
Bài tập 85 trang 65 SGK Toán 12 NC
Bài tập 86 trang 65 SGK Toán 12 NC
Bài tập 87 trang 65 SGK Toán 12 NC
Bài tập 88 trang 65 SGK Toán 12 NC
Bài tập 89 trang 65 SGK Toán 12 NC
Bài tập 90 trang 65 SGK Toán 12 NC
Bài tập 91 trang 65 SGK Toán 12 NC
Bài tập 92 trang 66 SGK Toán 12 NC
Bài tập 93 trang 66 SGK Toán 12 NC
Bài tập 94 trang 66 SGK Toán 12 NC
Bài tập 95 trang 66 SGK Toán 12 NC
Bài tập 96 trang 66 SGK Toán 12 NC
Bài tập 97 trang 67 SGK Toán 12 NC
Bài tập 98 trang 67 SGK Toán 12 NC





