Bài tập 78 trang 62 SGK Toán 12 NC

71 BT SGK

a) Vẽ đồ thị (P) của hàm số y = x² − x + 1 và đồ thị (H) của hàm số \(y = \frac{1}{{x + 1}}\)

b) Tìm giao điểm của hai đường cong (P) và (H). Chứng minh rằng hia đường cong đó có tiếp tuyến chung tại giao điểm của chúng.

c) Xác định các khoảng trên đó (P) nằm phía trên hoặc phía dưới (H).

Hướng dẫn giải chi tiết

a) Đồ thị

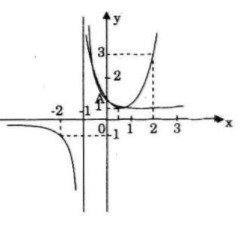
b) Hoành độ giao điể của parabol (P) và hypebol (H) là nghiệm của phương trình:

\(\begin{array}{l}
{x^2} - x + 1 = \frac{1}{{x + 1}}\\
\Leftrightarrow \left( {x + 1} \right)\left( {{x^2} - x + 1} \right) = 1
\end{array}\)

(vì x = -1 không là nghiệm của phương trình)

\( \Leftrightarrow {x^3} + 1 = 1 \Leftrightarrow x = 0;(y(0) = 1)\)

Giao điểm của (P) và (H) là A(0;1)

Đặt \(f(x) = {x^2} - x + 1;g(x) = \frac{1}{{x + 1}}\)

Ta có: \(f\prime (x) = 2x - 1;g\prime (x) = \frac{{ - 1}}{{{{(x + 1)}^2}}}\)

f′(0) = g′(x) = −1

Suy ra (P) và (H) có tiếp tuyến chung tại A nên (P) và (H) tiếp xúc nhau tại điểm A.

c) Xét hiệu \(f(x) - g(x) = {x^2} - x + 1 - \frac{1}{{x + 1}} = \frac{{{x^3}}}{{x + 1}}\)

Bảng xét dấu f(x) – g(x)

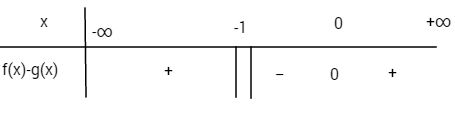
Trên các khoảng \(\left( { - \infty ; - 1} \right);\left( {0; + \infty } \right)\) (P) nằm phía trên (H). Trên khoảng (−1; 0) (P) nằm phía dưới (H).

-- Mod Toán 12 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 78 trang 62 SGK Toán 12 NC HAY thì click chia sẻ

YOMEDIA

Tìm giá trị của x và h để lượng vàng cần dùng nhỏ nhất?

bởi Phạm Khánh Ngọc 24/10/2018

Người ta muốn mạ vàng cho một cái hộp có đáy hình vuông, không nắp, thể tích hộp là 4 lít Giả sử độ dày lớp mạ tại mọi điểm trên một là như nhau.Gọi chiều cao và cạnh đáy hộp lần lượt là h và x. Giá trị của x và h để lượng vàng cần dùng nhỏ nhất

Theo dõi (0) 1 Trả lời
Chứng minh phân số a/(a-b) chưa tối giản

bởi Lê Trung Phuong 10/10/2018

Cho \(\dfrac{a}{b}\) là một phân số chưa tối giản . Chứng minh rằng các phân số sau chưa tối giản:

\(a\))\(\dfrac{a}{a-b};\)

\(b\))\(\dfrac{2a}{a-2b}\)

Các cậu giúp tôi với

Theo dõi (0) 1 Trả lời
Tìm x để hàm f(x)=-3(x-10)(x-4) có gái trị lớn nhất?

bởi Trần Phương Khanh 24/10/2018

giá trị của x sẽ là hàm f (x) = - 3 (x-10) (x-4) có giá trị lớn nhất? Tìm giá trị lớn nhất (gợi ý: viết hàm theo dạng chuẩn!)

Theo dõi (0) 1 Trả lời
Tìm mênh đề đúng, biết y=f(x) có đạo hàm f'(x)= (x^2-1)*(x+1)*(5-x)

bởi Nguyễn Trà Long 24/10/2018

giúp em với

Cho hàm số y=f(x) có đạo hàm f'(x)= (x^2-1)*(x+1)*(5-x). mệnh đề nào sau đây đúng:

A. f(1)<f(4)<f(2)

B. f(1)<f(2)<f(4)

C. f(2)<f(1)<f(4)

D. f(4)<f2<f1

Theo dõi (0) 1 Trả lời
Tìm m để pt -x^3-3x^2+4-3m=0 có 2 nghiệm phân biệt

bởi Nguyễn Tiểu Ly 24/10/2018

-X^3 - 3X^2 +4 -3m=0 tìm m để có 2 nghiệm phân biệt. giúp với ạ

Theo dõi (0) 1 Trả lời
Tìm m để (C_m) cắt trục Ox tại 3 điểm phân biệt

bởi Lê Minh Hải 24/10/2018

Anh chị em giải giúp e câu 10 trong hình với an, e cảm ơn nhiều ạ

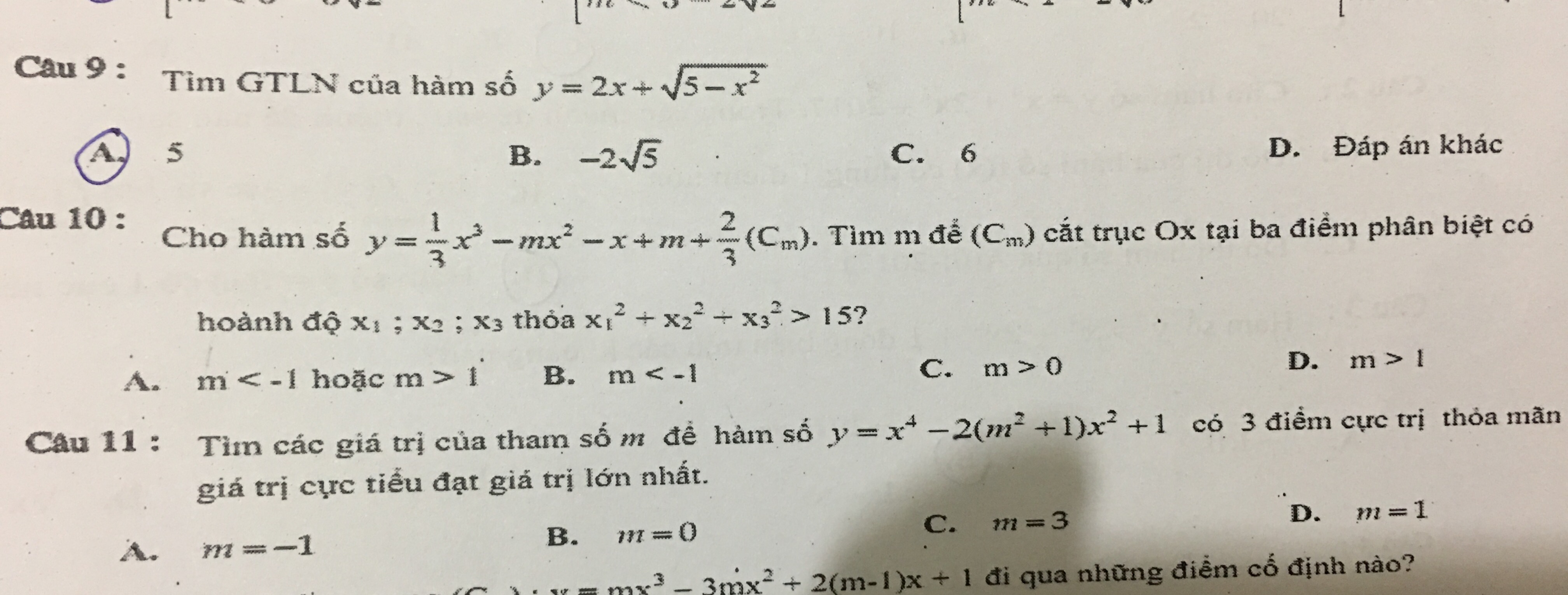Theo dõi (0) 1 Trả lời
Tìm điểm M trên (C): y=(2x+1)/(x-1) để khoảng cách từ A và B đến tiếp tuyến của (C)

bởi Nguyễn Vũ Khúc 24/10/2018

cho hàm số y=(2x+1)/(x-1) có đồ thị (C).Tìm các điểm M trên đồ thị (C) sao cho khoảng cách từ 2 điểm A(2;4) và B(-4;-2) đến tiếp tuyến của (C) tại M là bằng nhau.

Theo dõi (0) 1 Trả lời
Tìm nghiệm của pt (msinx-2)/(m-2cosx)=(mcosx-2)/(m-2sinx)

bởi Lê Minh Trí 24/10/2018

khi m≠+\(\sqrt{2}\) ≠-\(\sqrt{2}\) phương trình \(\dfrac{m\sin x-2}{m-2cosx}=\dfrac{m\cos x-2}{m-2\sin x}\) có bao nhiêu nghiệm thuộc đoạn \([20\pi;30\pi]\)

Theo dõi (0) 1 Trả lời