Bài tập 74 trang 62 SGK Toán 12 NC

a) TXĐ: D = R

\(\begin{array}{l}
f\prime (x) = 3{x^2} - 3\\
f\prime (x) = 0 \Leftrightarrow \left[ \begin{array}{l}
x = 1\\
x =  - 1
\end{array} \right.
\end{array}\)

Hàm số đồng biến trên khoảng: \(\left( { - \infty ; - 1} \right),(1; + \infty )\)

 Hàm số nghịch biến trên khoảng (−1;1)

+) Cực trị:

 Hàm số đạt cực đại tại x = −1; y(−1) = 3

 Hàm số đạt cực tiểu tại x = 1; y(1) = −1

+) Giới hạn:

\(\begin{array}{l}
\mathop {\lim}\limits_{x \to  + \infty } f(x) =  + \infty \\
\mathop {\lim}\limits_{x \to  - \infty } f(x) =  - \infty 
\end{array}\)

Bảng biến thiên 

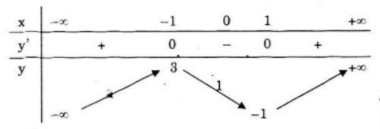
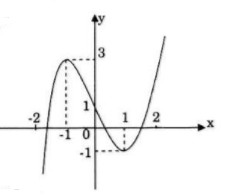
Đồ thị

Đồ thị giao trục $Oy$ tại điểm (0;1)

Hàm số đồ thị nhận I(0;1) làm tâm đối xứng

b)

\(\begin{array}{*{20}{l}}
{f\prime (x) = 3{x^2} - 3}\\
{f\prime \prime (x) = 6x,f\prime \prime (x) = 0 \Leftrightarrow x = 0}
\end{array}\)

f(0) = 0. Điểm uốn I(0;1)

Phương tiếp tuyến của (C) tại I là:

y − 1 = f′(0)(x −0) ⇔ y = −3x + 1

c) Phương trình đường thẳng (d_m) là y = mx  + 1

Hoành độ giao điểm của đường thẳng (d_m) và đường cong (C) là nghiệm của phương trình

\(\begin{array}{*{20}{l}}
\begin{array}{l}
{x^3} - 3x + 1 = mx + 1\\
 \Leftrightarrow {x^3} - (m + 3)x = 0
\end{array}\\
{ \Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 0}\\
{{x^2} = m + 3}
\end{array}} \right.}
\end{array}\)

(d_m) cắt (C) tại 3 điểm phân biệt khi và chỉ khi (1) có 3 nghiệm phân biệt, tức m + 3 > 0 ⇔ m > −3.

-- Mod Toán 12 HỌC247