Bài tập 72 trang 62 SGK Toán 12 NC
Cho hàm số: \(f\left( x \right) = {1 \over 3}{x^3} - 2{x^2} + {{17} \over 3}\)
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.
b) Chứng minh rằng phương trình f(x) = 0 có ba nghiệm phân biệt.
Hướng dẫn giải chi tiết
a)
TXĐ: \(D =\mathbb R\)
\(\eqalign{
& \mathop {\lim }\limits_{x \to + \infty } y = + \infty ;\,\mathop {\lim }\limits_{x \to - \infty } y = - \infty \cr
& f'\left( x \right) = {x^2} - 4x\cr&f'\left( x \right) = 0 \Leftrightarrow {x^2} - 4x = 0 \Leftrightarrow \left[ \matrix{
x = 0 \hfill \cr
x = 4 \hfill \cr} \right.\cr&f\left( 0 \right) = {{17} \over 3};\,f\left( 4 \right) = - 5 \cr} \)
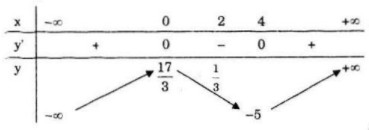
Hàm số đồng biến trên các khoảng (-∞,0) và (4; +∞)
Hàm số nghịch biến trên khoảng (0; 4)
Hàm số đạt cực đại tại x = 0; yCĐ=y(0)=17/3
Hàm số đạt cực tiểu tại x = 4, yCT=y(4)=-5
\(\eqalign{
& f''\left( x \right) = 2x - 4\cr&f''\left( x \right) = 0 \Leftrightarrow x = 2 \cr
& f\left( 2 \right) = {1 \over 3} \cr} \)
Điểm uốn \(I\left( {2;{1 \over 3}} \right)\)
Đồ thị nhận I làm tâm đối xứng.
Đồ thị:
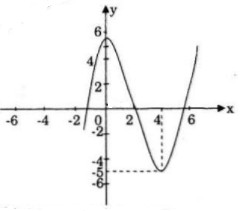
b.
Hàm số đã cho có giá trị cực đại và giá trị cực tiểu trái dấu, tức hai điểm cực đại và cực tiểu của đồ thị nằm về hai phía đối với trục hoành do đó đồ thị hàm số cắt trục hoành tại ba điểm phân biệt nên phương trình f(x) =0 có ba nghiệm phân biệt.
-- Mod Toán 12 HỌC247
-

 Các thầy cho em hỏi : Trên đồ thị hàm số y=f(x) có bao nhiêu điểm toạ độ là số dương ? Với dạng này thì em phải làm thế nào ạ ?Theo dõi (1) 0 Trả lời
Các thầy cho em hỏi : Trên đồ thị hàm số y=f(x) có bao nhiêu điểm toạ độ là số dương ? Với dạng này thì em phải làm thế nào ạ ?Theo dõi (1) 0 Trả lời -


Tìm tập xác định của y= căn(log_2(3-2x-x^2)/(x+1)))
bởi Pé Hânn
 04/12/2019
Giải hộ e vs ai
04/12/2019
Giải hộ e vs ai Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Có bao nhiêu giá trị nguyên của m để phương trình x^3-3x^2=m +3 có 3 nghiệm phân biệt ?
bởi Liu Ly
 30/11/2019
Câu 24
30/11/2019
Câu 24 Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tình GTNN của P=2 căn x+1/(căn x+1)
bởi Lương Thùy Linh
 23/11/2019
23/11/2019
Tìm giá trị nhỏ nhất của
Theo dõi (0) 3 Trả lời -


Định m để đồ thị hàm số y=x^3 -mx^2 +1 cắt trục hoành đúng 2 điểm phân biệt
bởi Nguyễn Văn Hoàng
 18/11/2019
18/11/2019
Định m để đồ thị hàm số y=x^3 -mx^2 +1 cắt trục hoành đúng 2 điểm phân biệt
Theo dõi (0) 2 Trả lời -


 Theo dõi (0) 8 Trả lời
Theo dõi (0) 8 Trả lời -


Tìm m để đồ thị hàm số y=(x^2-x+m^2)/(x-1) có các điểm cực trị A, B và AB^2=20
bởi Nguyễn Thái Phong
 18/10/2019
18/10/2019
 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời
Bài tập SGK khác
Bài tập 70 trang 61 SGK Toán 12 NC
Bài tập 71 trang 62 SGK Toán 12 NC
Bài tập 73 trang 62 SGK Toán 12 NC
Bài tập 74 trang 62 SGK Toán 12 NC
Bài tập 75 trang 62 SGK Toán 12 NC
Bài tập 76 trang 62 SGK Toán 12 NC
Bài tập 77 trang 62 SGK Toán 12 NC
Bài tập 78 trang 62 SGK Toán 12 NC
Bài tập 79 trang 62 SGK Toán 12 NC
Bài tập 80 trang 64 SGK Toán 12 NC
Bài tập 81 trang 64 SGK Toán 12 NC
Bài tập 82 trang 64 SGK Toán 12 NC
Bài tập 83 trang 64 SGK Toán 12 NC
Bài tập 84 trang 65 SGK Toán 12 NC
Bài tập 85 trang 65 SGK Toán 12 NC
Bài tập 86 trang 65 SGK Toán 12 NC
Bài tập 87 trang 65 SGK Toán 12 NC
Bài tập 88 trang 65 SGK Toán 12 NC
Bài tập 89 trang 65 SGK Toán 12 NC
Bài tập 90 trang 65 SGK Toán 12 NC
Bài tập 91 trang 65 SGK Toán 12 NC
Bài tập 92 trang 66 SGK Toán 12 NC
Bài tập 93 trang 66 SGK Toán 12 NC
Bài tập 94 trang 66 SGK Toán 12 NC
Bài tập 95 trang 66 SGK Toán 12 NC
Bài tập 96 trang 66 SGK Toán 12 NC
Bài tập 97 trang 67 SGK Toán 12 NC
Bài tập 98 trang 67 SGK Toán 12 NC





