Bài tập 1.79 trang 40 SBT Toán 12

a) TXĐ: D = R.

Chiều biến thiên:

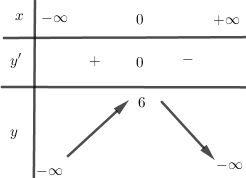
Ta có: \(y' =  - 4{x^3} - 2x =  - 2x\left( {2{x^2} + 1} \right);\)

\(y' = 0 \Leftrightarrow x = 0\)

Hàm số nghịch biến trên \(\left( {0; + \infty } \right)\) và đồng biến trên \(\left( { - \infty ;0} \right)\).

Hàm số đạt cực đại tại \(x = 0;{y_{CD}} = 6\) và không có cực tiểu.

Bảng biến thiên:

Đồ thị:

Đồ thị đi qua các điểm (1;4) và (−1;4), cắt trục hoành tại hai điểm \(\left( { \pm \sqrt 2 ;0} \right)\)

b) Ta có: \(y' =  - 4{x^3} - 2x\)

Vì tiếp tuyến vuông góc với đường thẳng \(y = \frac{1}{6}x - 1\)$\mathrm{}$ nên tiếp tuyến có hệ số góc là −6.

Ta có: \( - 4{x^3} - 2x =  - 6 \Leftrightarrow 2{x^3} + x - 3 = 0\)

\(\begin{array}{*{20}{l}}
\begin{array}{l}
 \Leftrightarrow 2({x^3} - 1) + (x - 1) = 0\\
 \Leftrightarrow \left( {x - 1} \right)\left( {2{x^2} + 2x + 3} \right) = 0
\end{array}\\
{ \Leftrightarrow x = 1{\mkern 1mu} {\mkern 1mu} \left( {2{x^2} + 2x + 3 > 0,\forall x} \right)}
\end{array}\)

Suy ra y(1) = 4.

Phương trình tiếp tuyến là: 

\(y =  - 6\left( {x - 1} \right) + 4\) hay \(y =  - 6x + 10\).

-- Mod Toán 12 HỌC247