Bài tập 69 trang 61 SGK Toán 12 NC
Xét chiều biến thiên và tìm cực trị (nếu có) của các hàm số sau:
\(\begin{array}{l}
a)y = \sqrt {3x + 1} \\
b)y = \sqrt {4x - {x^2}} \\
c)y = x + \sqrt x \\
d)y = x - \sqrt x
\end{array}\)
Hướng dẫn giải chi tiết
a) TXĐ: \(D = \left[ { - \frac{1}{3}; + \infty } \right)\)
\(y\prime = \frac{3}{{2\sqrt {3x + 1} }} > 0,\forall x > - \frac{1}{3}\)
Hàm số đồng biến trên khoảng \(\left( { - \frac{1}{3}; + \infty } \right)\), hàm số không có cực trị
b) TXĐ: D = [0;4]
\(\begin{array}{l}
y\prime = \frac{{4 - 2x}}{{2\sqrt {4x - {x^2}} }};\\
y\prime = 0 \Leftrightarrow x = 2;y(2) = 2
\end{array}\)
Bảng biến thiên
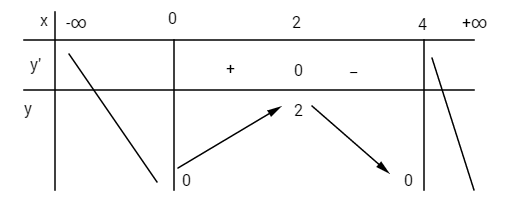
Hàm số đạt cực đại tại điểm x = 2; giá trị cực đại y(2) = 2.
c) TXĐ: \(D = [0; + \infty )\)
\(\begin{array}{l}
y\prime = 1 + \frac{1}{{2\sqrt x }} = \frac{{2\sqrt x + 1}}{{2\sqrt x }}\\
y\prime = 1 + \frac{1}{{2\sqrt x }} > 0,\forall x > 0
\end{array}\)
Hàm số đồng biến trên khoảng \((0; + \infty )\), hàm số không có cực trị.
d) TXĐ: \(D = [0; + \infty )\)
\(\begin{array}{l}
y' = 1 - \frac{1}{{2\sqrt x }}\\
y\prime = 0 \Leftrightarrow x = \frac{1}{4}
\end{array}\)
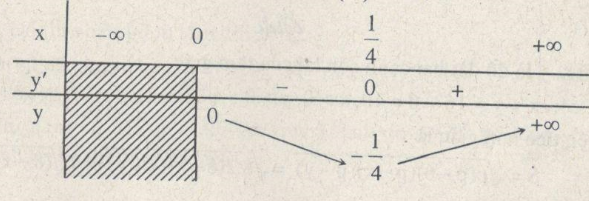
Hàm số đạt cực tiểu tại điểm \(x = \frac{1}{4}\), giá trị cực tiểu \(y\left( {\frac{1}{4}} \right) = - \frac{1}{4}\)
-- Mod Toán 12 HỌC247
-

 Ôn tập kiến thức toán
Ôn tập kiến thức toán Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tính đạo hàm của hàm số y=(x^4-3x^2-1)^3/7
bởi Dũng Văn
 16/02/2020
Giải giúp em cau 10 ạ
16/02/2020
Giải giúp em cau 10 ạ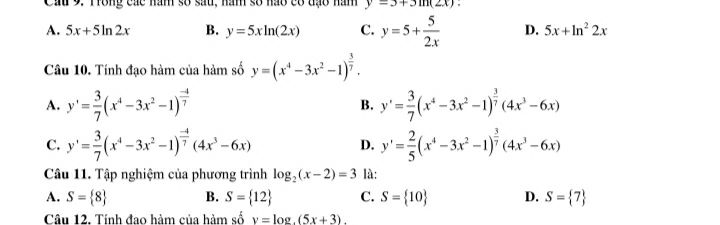 Theo dõi (0) 9 Trả lời
Theo dõi (0) 9 Trả lời -


 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm tất cả các giá trị thực của tham số m để hàm số y=2x^3+3(m−1)x^2+6(m−2)x+2017 nghịch biến trên khoảng (a;b) sao cho b-a > 3
bởi Phạm Đạt
 10/02/2020
10/02/2020
Tìm tất cả các giá trị thực của tham số m để hàm số y=2x3+3(m−1)x2+6(m−2)x+2017y=2x3+3(m−1)x2+6(m−2)x+2017 nghịch biến trên khoảng (a;b) sao cho b-a>3.
Theo dõi (0) 0 Trả lời -


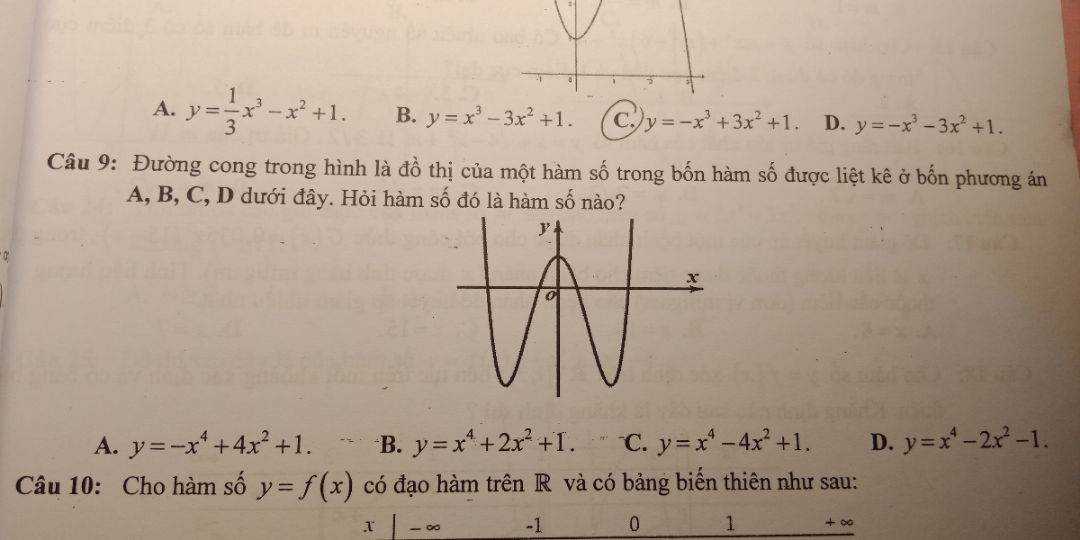 Theo dõi (0) 5 Trả lời
Theo dõi (0) 5 Trả lời -


Nêu sơ đồ khảo sát sự biến thiên và vẽ đồ thị hàm số
bởi Huỳnh Trân
 09/01/2020
09/01/2020
Nêu sơ đồ khảo sát sự biến thiên và vẽ đồ thị hàm số.
Theo dõi (0) 1 Trả lời -


Phát biểu các điều kiện cần và đủ để hàm số f(x) đơn điệu trên một khoảng.
Theo dõi (0) 1 Trả lời -


Định nghĩa sự đơn điệu (đồng biến, nghịch biến) của một hàm số trên một khoảng
bởi Huỳnh Trân
 08/01/2020
08/01/2020
Định nghĩa sự đơn điệu (đồng biến, nghịch biến) của một hàm số trên một khoảng.
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 1.96 trang 43 SBT Toán 12
Bài tập 68 trang 61 SGK Toán 12 NC
Bài tập 70 trang 61 SGK Toán 12 NC
Bài tập 71 trang 62 SGK Toán 12 NC
Bài tập 72 trang 62 SGK Toán 12 NC
Bài tập 73 trang 62 SGK Toán 12 NC
Bài tập 74 trang 62 SGK Toán 12 NC
Bài tập 75 trang 62 SGK Toán 12 NC
Bài tập 76 trang 62 SGK Toán 12 NC
Bài tập 77 trang 62 SGK Toán 12 NC
Bài tập 78 trang 62 SGK Toán 12 NC
Bài tập 79 trang 62 SGK Toán 12 NC
Bài tập 80 trang 64 SGK Toán 12 NC
Bài tập 81 trang 64 SGK Toán 12 NC
Bài tập 82 trang 64 SGK Toán 12 NC
Bài tập 83 trang 64 SGK Toán 12 NC
Bài tập 84 trang 65 SGK Toán 12 NC
Bài tập 85 trang 65 SGK Toán 12 NC
Bài tập 86 trang 65 SGK Toán 12 NC
Bài tập 87 trang 65 SGK Toán 12 NC
Bài tập 88 trang 65 SGK Toán 12 NC
Bài tập 89 trang 65 SGK Toán 12 NC
Bài tập 90 trang 65 SGK Toán 12 NC
Bài tập 91 trang 65 SGK Toán 12 NC
Bài tập 92 trang 66 SGK Toán 12 NC
Bài tập 93 trang 66 SGK Toán 12 NC
Bài tập 94 trang 66 SGK Toán 12 NC
Bài tập 95 trang 66 SGK Toán 12 NC
Bài tập 96 trang 66 SGK Toán 12 NC
Bài tập 97 trang 67 SGK Toán 12 NC
Bài tập 98 trang 67 SGK Toán 12 NC





