Bài tập 97 trang 67 SGK Toán 12 NC
Xét phương trình \({x^3} + 3{x^2} = m\)
(A) Với m = 5, phương trình đã có ba nghiệm;
(B) Với m = -1, phương trình có hai nghiệm.
(C) Với m = 4, phương trình đã có ba nghiệm phân biệt;
(D) Với m = 2, phương trình đã có ba nghiệm phân biệt.
Hướng dẫn giải chi tiết
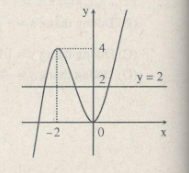
Vẽ đồ thị hàm số \(y = {x^3} + 3{x^2}\)
\(\begin{array}{l}
y' = 3{x^2} + 6x;y' = 0\\
\Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x = - 2;y\left( { - 2} \right) = 4}\\
{x = 0;y\left( 0 \right) = 0}
\end{array}} \right.
\end{array}\)
m = 2: Phương trình có 3 nghiệm phân biệt.
Chọn (D).
-- Mod Toán 12 HỌC247
-


Cho hàm số \(y=x^{3}-6x^{2}+9x-1\; \; (1).\)
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1).
2. Tìm m để phương trình \(x(x-3)^{2}=m\) có 3 nghiệm phân biệt.
Theo dõi (0) 1 Trả lời -


Cho \((C): y = - x^3+6x^2-9x+3\) có 3 nghiệm phân biệt
a) Khảo sát sự biến thiên và vẽ đồ thị (C).
b) Tìm m để phương trình: \(x^3-6x^2+9x-4+2m=0\) có 3 nghiệm phân biệt.Theo dõi (0) 1 Trả lời -


Giải bất phương trình: \(e^{1+\sqrt{e}}+\sqrt{1+\sqrt{x}}+\frac{1}{\sqrt{1+\sqrt{x}}}> e^{2x-4\sqrt{x}+3}+\frac{1}{\sqrt{2x-4\sqrt{x}}+3}\)
bởi Việt Long
 08/02/2017
08/02/2017
Giải bất phương trình: \(e^{1+\sqrt{e}}+\sqrt{1+\sqrt{x}}+\frac{1}{\sqrt{1+\sqrt{x}}}> e^{2x-4\sqrt{x}+3}+\frac{1}{\sqrt{2x-4\sqrt{x}}+3}\)
Theo dõi (0) 1 Trả lời -


Tìm các giá trị của m để đường thẳng y = mx + 2m + 1 cắt (C) tại hai điểm phân biệt A, B
bởi Nguyễn Thị Thu Huệ
 07/02/2017
07/02/2017
Cho hàm số \(y=\frac{2x+1}{x+1}\). Tìm các giá trị của m để đường thẳng y = mx + 2m + 1 cắt (C) tại hai điểm phân biệt A, B.Với giá trị nào của m thì khoảng cách từ hai điểm A và B đến trục hoành bằng nhau.
Theo dõi (0) 1 Trả lời -


Cho hàm số \(y=\frac{x+1}{x-1}\) có đồ thị (H). Tìm m để đường thẳng d: y = -x + m cắt (H) tại hai điểm phân biệt.
Theo dõi (0) 1 Trả lời -


Tìm các giá trị của tham số m để phương trình \(\small x^3-3x^2-2m=0\) có 3 nghiệm phân biệt.
bởi Nguyễn Tiểu Ly
 07/02/2017
07/02/2017
Cho hàm số \(\small y=x^3-3x^2+1 \ \ \ \ (C)\)
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số (C).
b) Tìm các giá trị của tham số m để phương trình \(\small x^3-3x^2-2m=0\) có 3 nghiệm phân biệt.Theo dõi (0) 1 Trả lời -


Cho hàm số \(y=x^{3}-3x^{2}+2\)
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số. Chứng minh rằng điểm uốn là tâm đối xứng của đồ thị.
b) Có tồn tại hay không tiếp tuyến của đồ thị có hệ số góc k < -3. Chứng minh rằng có duy nhất một tiếp tuyến của đồ thị đi qua điểm uốn.
Theo dõi (0) 1 Trả lời -


Dựa vào đồ thị (C), tìm tất cả các giá trị của m để phương trình \(-x^3+3x+m-3=0\) có 3 nghiệm phân biệt
bởi Naru to
 08/02/2017
08/02/2017
Cho hàm số \(y=-x^3+3x+1\)
a/ Khảo sát sự biến thiên và vẽ đồ thị của hàm số (C).
b/ Dựa vào đồ thị (C), tìm tất cả các giá trị của m để phương trình \(-x^3+3x+m-3=0\) có 3 nghiệm phân biệt.Theo dõi (0) 2 Trả lời






