Bài tập 92 trang 66 SGK Toán 12 NC
Giá trị lớn nhất của hàm số \(f\left( x \right) = \sqrt { - {x^2} - 2x + 3} \) là:
(A) 2
(B) \(\sqrt 2 \)
(C) 0
(D) 3.
Hướng dẫn giải chi tiết
TXĐ: D = [−3;1]
\(\begin{array}{l}
f'\left( x \right) = \frac{{ - 2x - 2}}{{2\sqrt { - {x^2} - 2x + 3} }}\\
= - \frac{{x + 1}}{{\sqrt { - {x^2} - 2x + 3} }}\\
f'\left( 0 \right) \Leftrightarrow x = - 1f\left( { - 1} \right) = 2
\end{array}\)
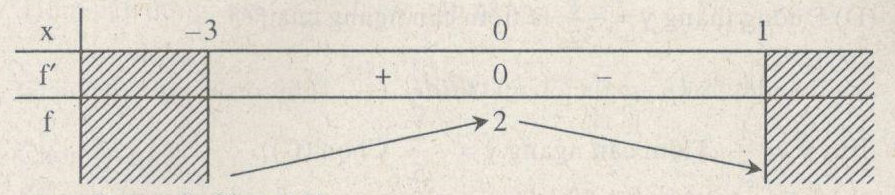
\(\mathop {\max }\limits_{x \in \left[ { - 3;1} \right]} f\left( x \right) = 2\)
Chọn (A).
-- Mod Toán 12 HỌC247
-
Tìm các giá trị của tham số m để phương trình \(x^2(x^2-2)+3=m\) có 2 nghiệm phân biệt
bởi thanh hằng
06/02/2017
Cho hàm số \(y = x^4-2x^2+4\)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1).
b) Tìm các giá trị của tham số m để phương trình \(x^2(x^2-2)+3=m\) có 2 nghiệm phân biệt.
Theo dõi (0) 1 Trả lời -
Viết phương trình tiếp tuyến với đồ thị (C), biết tiếp tuyến vuông góc với đường thẳng \(y=-\frac{1}{9}x\)
bởi Tieu Dong
07/02/2017
Cho hàm số \(y=x^3+3x^2-2\) (1)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số
b) Viết phương trình tiếp tuyến với đồ thị (C), biết tiếp tuyến vuông góc với đường thẳng \(y=-\frac{1}{9}x\)Theo dõi (0) 5 Trả lời -
Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp điểm có hoành độ x = 1
bởi Nguyễn Sơn Ca
07/02/2017
Cho hàm số \(\small y = \frac{2x-1}{x+1}\)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho.
b) Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp điểm có hoành độ x = 1.Theo dõi (0) 1 Trả lời
