Bài tập 79 trang 62 SGK Toán 12 NC
Cho hàm số: \(y = f\left( x \right) = x + \frac{1}{x}\)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
b) Tiếp tuyến của đường cong (C) tại điểm \(M\left( {{x_0};f\left( {{x_0}} \right)} \right)\) cắt tiệm cận đứng và tiệm cận xiên tại hai điểm A và B. Chứng minh rằng M là trung điểm của đoạn thẳng AB và tam giác OAB có diện tích không phụ thuộc vào vị trí điểm M trên đường cong (C).
Hướng dẫn giải chi tiết
a) Tập xác định: D = R∖{0}
\(\begin{array}{l}
y\prime = 1 - \frac{1}{{{x^2}}} = \frac{{{x^2} - 1}}{{{x^2}}}\\
y\prime = 0 \Leftrightarrow x = \pm 1
\end{array}\)
Hàm số đồng biến trên khoảng: \(( - \infty ; - 1);(1; + \infty )\)
Hàm số nghịch biến trên khoảng: (−1; 0); (0; 1)
+) Cực trị:
Hàm số đạt cực đại tại: x = −1; y(−1) = −2
Hàm số đạt cực tiểu tại: x = 1; y(1) = 2
+) Giới hạn:
\(\mathop {\lim y}\limits_{x \to {0^ - }} = - \infty ;\mathop {\lim y}\limits_{x \to {0^ + }} = + \infty \)
Tiệm cận đứng: x = 0
\(\begin{array}{l}
\mathop {\lim}\limits_{x \to \pm \infty } y = \pm \infty \\
\mathop {\lim}\limits_{x \to \infty } (y - x) = \mathop {\lim}\limits_{x \to \infty } \frac{1}{x} = 0
\end{array}\)
Tiệm cận xiên: y = x
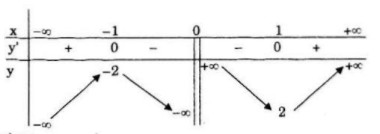
Bảng biến thiên:
Đồ thị:
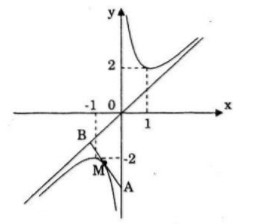
b) Tiệm cận đứng x = 0; Tiệm cận xiên y = x.
Ta có \(f(x) = 1 - \frac{1}{{{x^2}}}\).
Phương trình tiếp tuyến của đường cong (C) tại điểm \(M\left( {{x_o};f\left( {{x_o}} \right)} \right)\) là:
\(y = \left( {1 - \frac{1}{{x_0^2}}} \right)(x - {x_0}) + {x_0} + \frac{1}{{{x_0}}}\)
Thay x = 0 vào phương trình trên, ta được tung độ của điểm A:
\({y_A} = \left( {1 - \frac{1}{{x_0^2}}} \right)\left( { - {x_0}} \right) + {x_0} + \frac{1}{{{x_0}}} = \frac{2}{{{x_0}}}\)
Vậy \(A\left( {0;\frac{2}{{{x_0}}}} \right)\)
Hoành độ của điểm B là nghiệm của phương trình
\(\begin{array}{l}
\left( {1 - \frac{1}{{x_0^2}}} \right)(x - {x_0}) + {x_0} + \frac{1}{{{x_0}}} = x\\
\Leftrightarrow - \frac{x}{{{x_0}}} + \frac{2}{{{x_0}}} = 0 \Leftrightarrow x = 2{x_0}
\end{array}\)
xB = 2x0. Vậy B(2x0; 2x0)
Ta có: \({x_M} = {x_0} = \frac{{0 + 2{x_0}}}{2} = \frac{{{x_A} + {x_B}}}{2}\)
Vì ba điểm A, M, B thẳng hàng nên từ đó suy ra rằng M là trung điểm của đoạn thẳng AB.
Diện tích tam giác OAB là:
\(\begin{array}{l}
S = \frac{1}{2}\left| {{y_A}} \right|.\left| {{y_B}} \right|\\
= \frac{1}{2}\left| {\frac{2}{{{x_0}}}} \right|.\left| {2{x_0}} \right| = 2,\forall {x_0} \ne 0
\end{array}\)
-- Mod Toán 12 HỌC247
-


Tìm m đẻ pt |2x^2-3x-2|=5m-8x-2x^2| có nghiệm duy nhất
bởi Hoàng My
 24/10/2018
24/10/2018
tìm m để phương trình sau có nghiệm duy nhất
\(\left|2x^2-3x-2\right|=5m-8x-2x^2\)
help me
Theo dõi (0) 1 Trả lời -


Tìm m để hàm số y=mx^3-2x^2+3mx+2016 luôn nghịch biến
bởi My Hien
 24/10/2018
24/10/2018
cho hàm số y = m.x3 - 2x2 + 3mx +2016 . tìm tất cả các giá trị của tham số m để hàm số luôn nghịc biến?
Theo dõi (0) 1 Trả lời -


Mọi người giúp mình câu này với! Mình cảm ơn!
Gọi K là tập hợp tất cả các giá trị của tham số m để phương trình sin2x + \(\sqrt{2}\)sin(x+\(\dfrac{\pi}{4}\)) - 2 = m có đúng hai nghiệm thuộc khoảng (0;\(\dfrac{3\pi}{4}\)). Tìm K ??
Theo dõi (0) 1 Trả lời -


Hàm số y=f(x+2) đồng biến trên khoảng nào biết f(x) đồng biến trên (-1;2)
bởi Nguyễn Lê Tín
 24/10/2018
24/10/2018
Nếu hàm số f(x) đồng biến trên khoảng (-1;2) thì hàm số y=f(x+2) đồng biến trên khoảng nào?
A. (-1;2)
B. (1;4)
C. (-3;0)
D. (-2;4)
giúp em với
Theo dõi (0) 2 Trả lời -


Tìm điểm M thuộc đò thị (C): x^3-3x^2-2
bởi Thu Hang
 24/10/2018
24/10/2018
Câu 1: Tìm điểm M thuộc đò thị(c): \(y= x^3-3x^2-2\) biết hệ số góc của tiếp tuyến với (c) tại M bằng 9
A.M(1;-6),M(-3;-2) B.M(-1;-6),M(3;-2) C.M(-1;-6),M(-3;-2) D.M(1;6),M(3;2)
Câu 2: Tiếp tuyến với đồ thị hàm số \(y=\frac{1}{3}x^3-2x^2+3x+4\) biết tiếp tuyến song song với đt d:y= \(3x-\frac{20}{3}\) là:
A.y=3x+4;y=\(3x-\frac{20}{3}\) B.y=3x-4;y=\(3x-\frac{40}{3}\) C.y=3x+4 D.y=3x-4
Câu 3: có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (0;10) đẻ đường thẳng d:y=-x+m cắt đò thị hàm số \(y=\frac{2x+1}{x-1}\)tại hai điểm phan biệt
A.5 B.6 C.7 D.8
Câu 4: Đặt a=log126, b=log12 7. Hãy biểu diễn log27 theo a và b
\(A.\frac{a}{b+1} B.\frac{b}{1-a} C.\frac{a}{b-1} D.\frac{b}{a+1}\)
Theo dõi (0) 1 Trả lời -


Tìm m để đồ thị hàm số: y=mx cắt đồ thị y= x3-3x2 tại ba điểm phân biệt trong đó có hai điểm có hoành độ dương
Theo dõi (0) 1 Trả lời -


Tìm x để diện tích S(x) nhỏ nhất biết S(x) là diện tích mảnh tôn làm hộp không nắp
bởi Nguyễn Hoài Thương
 24/10/2018
24/10/2018
Một hộp không nắp được làm từ một mảnh tôn có diện tích là S(x). Hộp có đáy là một hình vuông có cạnh x(cm), chiều cao h(cm) và thể tích là 500cm3. Tìm x sao cho S (x) nhỏ nhất.
A.x=50 (cm) B.x=10 (cm) C.x=100 (cm) D.x=20 (cm)
Theo dõi (0) 1 Trả lời -


Tìm tọa độ nguyên của (C): y=(x+3)/(2x+1)
bởi Lan Anh
 24/10/2018
24/10/2018
(C) : y= \(\dfrac{x+3}{2x+1}\)có bao nhiêu toạ độ nguyên?
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 77 trang 62 SGK Toán 12 NC
Bài tập 78 trang 62 SGK Toán 12 NC
Bài tập 80 trang 64 SGK Toán 12 NC
Bài tập 81 trang 64 SGK Toán 12 NC
Bài tập 82 trang 64 SGK Toán 12 NC
Bài tập 83 trang 64 SGK Toán 12 NC
Bài tập 84 trang 65 SGK Toán 12 NC
Bài tập 85 trang 65 SGK Toán 12 NC
Bài tập 86 trang 65 SGK Toán 12 NC
Bài tập 87 trang 65 SGK Toán 12 NC
Bài tập 88 trang 65 SGK Toán 12 NC
Bài tập 89 trang 65 SGK Toán 12 NC
Bài tập 90 trang 65 SGK Toán 12 NC
Bài tập 91 trang 65 SGK Toán 12 NC
Bài tập 92 trang 66 SGK Toán 12 NC
Bài tập 93 trang 66 SGK Toán 12 NC
Bài tập 94 trang 66 SGK Toán 12 NC
Bài tập 95 trang 66 SGK Toán 12 NC
Bài tập 96 trang 66 SGK Toán 12 NC
Bài tập 97 trang 67 SGK Toán 12 NC
Bài tập 98 trang 67 SGK Toán 12 NC






