Bài tập 83 trang 64 SGK Toán 12 NC
Hàm số \(f\left( x \right) = {x^3} - 3{x^2} - 9x + 11\)
(A) Nhận điểm x = -1 làm điểm cực tiểu;
(B) Nhận điểm x = 3 làm điểm cực đại;
(C) Nhận điểm x = 1 làm điểm cực đại;
(D) Nhận điểm x = 3 làm điểm cực tiểu.
Hướng dẫn giải chi tiết
\(\begin{array}{l}
f'\left( x \right) = 3{x^2} - 6x - 9\\
f'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x = - 1}\\
{x = 3}
\end{array}} \right.
\end{array}\)
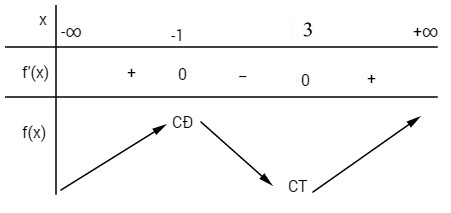
Hàm số đạt cực tiểu tại điểm x = 3.
Chọn D.
-- Mod Toán 12 HỌC247
-


Cho hàm số: \(y=x^3+3x^2+1\) (C). Đường thẳng d đi qua điểm A(-3;1) và có hệ số góc bằng k. Xác định k để đường thẳng đó cắt đồ thị (C) tại 3 điểm phân biệt
Theo dõi (0) 1 Trả lời -


Cho y=\(\dfrac{2x-1}{x-1}\) (C) . Tìm m để d:y=x+m cắt (C)tại 2 điểm phân biệt sao cho tam giác OAB vuông tại A hoặc B
Theo dõi (0) 1 Trả lời -


Tìm m để y=m(x-5)+10 cắt đồ thị (C): y=(x^2-2x+9)/(x-2) tại 2 điểm phân biệt A, B
bởi Cam Ngan
 24/10/2018
24/10/2018
Cho hàm số y=\(\dfrac{x^2-2x+9}{x-2}\) (C). Tìm m để y=m(x-5)+10 cắt đồ thị (C) tại 2 điểm phân biệt A, B sao cho M(5;10) là trung điểm AB
Theo dõi (0) 1 Trả lời -


Cho hàm số y=\(\dfrac{-x^2+2x-4}{x-2}\) (C). Định m để y =m cắt (C) tại 2 điểm phân biệt A, B sao cho diện tích tam giác 0AB=3
Theo dõi (0) 1 Trả lời -


Cho hàm số y=\(x^4-\left(3m+2\right)x^2+3m\) (Cm). Tìm m để y=-1 cắt (Cm) tại 4 điểm phân biệt đều có hoành độ nhỏ hơn 2
Theo dõi (0) 1 Trả lời -


Cho hàm số \(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{x^3-4x^2+3}{x-1};\left(x\ne1\right)\\ax+\dfrac{5}{2};\left(x=1\right)\end{matrix}\right.\). Xác định \(a\) để hàm số liên tục trên \(R\)?
A. \(a=\dfrac{5}{2}\). B. \(a=-\dfrac{15}{2}\). C. \(a=-\dfrac{5}{2}\). D. \(a=\dfrac{15}{2}\). Theo dõi (0) 1 Trả lời -


viết phương trinh tiếp tuyến của đồ thị y=\(\dfrac{3x-2}{x-2}\) tạo với 2 trục tọa độ một tam giác cân là
Theo dõi (0) 1 Trả lời -


Xét tính đơn điệu của hàm số y=căn 6 - x-x^2
bởi Quế Anh
 24/10/2018
24/10/2018
Xét tính đơn điệu của Hàm số : căn(6 - x - x2
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 81 trang 64 SGK Toán 12 NC
Bài tập 82 trang 64 SGK Toán 12 NC
Bài tập 84 trang 65 SGK Toán 12 NC
Bài tập 85 trang 65 SGK Toán 12 NC
Bài tập 86 trang 65 SGK Toán 12 NC
Bài tập 87 trang 65 SGK Toán 12 NC
Bài tập 88 trang 65 SGK Toán 12 NC
Bài tập 89 trang 65 SGK Toán 12 NC
Bài tập 90 trang 65 SGK Toán 12 NC
Bài tập 91 trang 65 SGK Toán 12 NC
Bài tập 92 trang 66 SGK Toán 12 NC
Bài tập 93 trang 66 SGK Toán 12 NC
Bài tập 94 trang 66 SGK Toán 12 NC
Bài tập 95 trang 66 SGK Toán 12 NC
Bài tập 96 trang 66 SGK Toán 12 NC
Bài tập 97 trang 67 SGK Toán 12 NC
Bài tập 98 trang 67 SGK Toán 12 NC






