Bài tập 70 trang 61 SGK Toán 12 NC
Người ta định làm một cái hộp hình trụ bằng tôn có thể tích V cho trước. Tìm bán kính đáy r và chiều cao của hình trụ sao cho tốn ít nguyên liệu nhất.
Hướng dẫn giải chi tiết
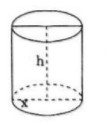
Thể tích của hình trụ là:
\(V = B.h = \pi {r^2}.h \Rightarrow h = \frac{V}{{\pi {r^2}}}\)
Diện tích toàn phần của hình trụ là:
\(\begin{array}{l}
S = 2\pi {r^2} + 2\pi r.h\\
= 2\pi {r^2} + 2\pi .r.\frac{V}{{\pi {r^2}}} = 2\pi {r^2} + \frac{{2V}}{r}
\end{array}\)
Xét hàm số:
\(\begin{array}{l}
S(r) = 2\pi {r^2} + \frac{{2V}}{r}(r > 0)\\
S\prime = 4\pi r - \frac{{2V}}{{{r^2}}} = \frac{{4\pi {r^2} - 2V}}{{{r^2}}}\\
S\prime = 0 \Leftrightarrow r = \sqrt[3]{{\frac{V}{{2\pi }}}}
\end{array}\)
Bảng biến thiên:
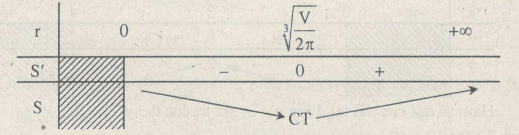
S đạt giá trị nhỏ nhất tại điểm \(r = \sqrt[3]{{\frac{V}{{2\pi }}}}\) khi đó:
\(h = \frac{V}{{\pi {r^2}}} = \frac{V}{{{\pi ^3}\sqrt {\frac{{{V^2}}}{{4{\pi ^2}}}} }} = \sqrt[3]{{\frac{V}{{2\pi }}}}\)
-- Mod Toán 12 HỌC247
-


Tìm m để phương trình 2sin^2(x)+msin2x= 2m vô nghiệm
bởi Nguyễn Lan
 06/01/2020
Tìm m để phương trình vô nghiệmTheo dõi (0) 0 Trả lời
06/01/2020
Tìm m để phương trình vô nghiệmTheo dõi (0) 0 Trả lời -


Có bao nhiêu bộ (m;n) sao cho pt g(x)=7 có 3 nghiệm phân biệt thuộc (0;8)?
bởi Quốc Ngoan
 04/01/2020
04/01/2020
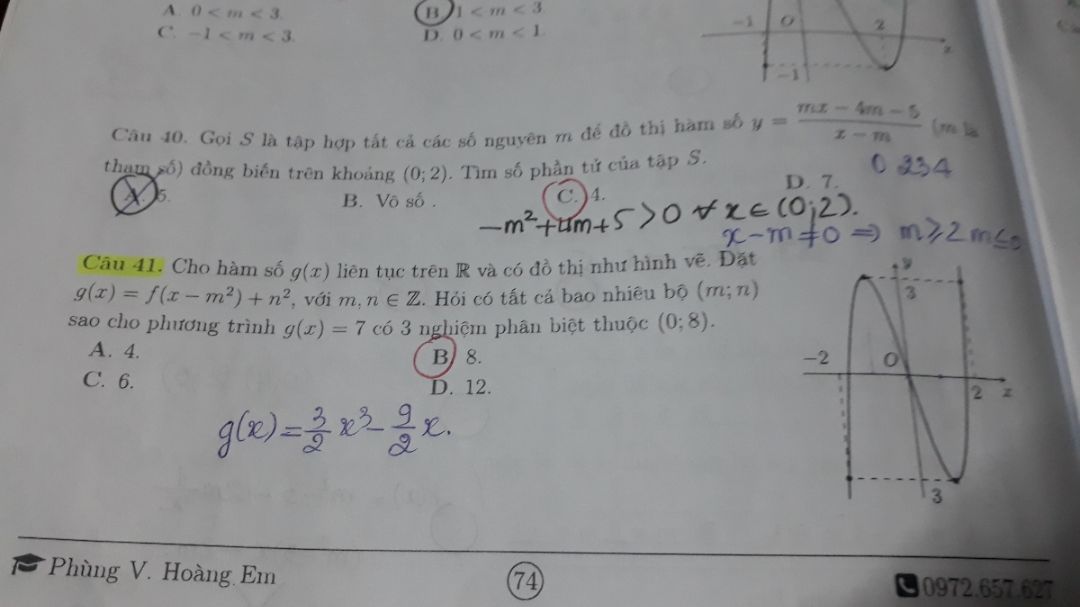 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 Hh
Hh Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Hàm số y=x^3+mx^2-m đồng biến trên khoảng (1;2) thì m thuộc khoảng nào sau đây?
bởi Ánh Trương
 25/12/2019
Mn giúp mình câu 25 với
25/12/2019
Mn giúp mình câu 25 với Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -

 .
.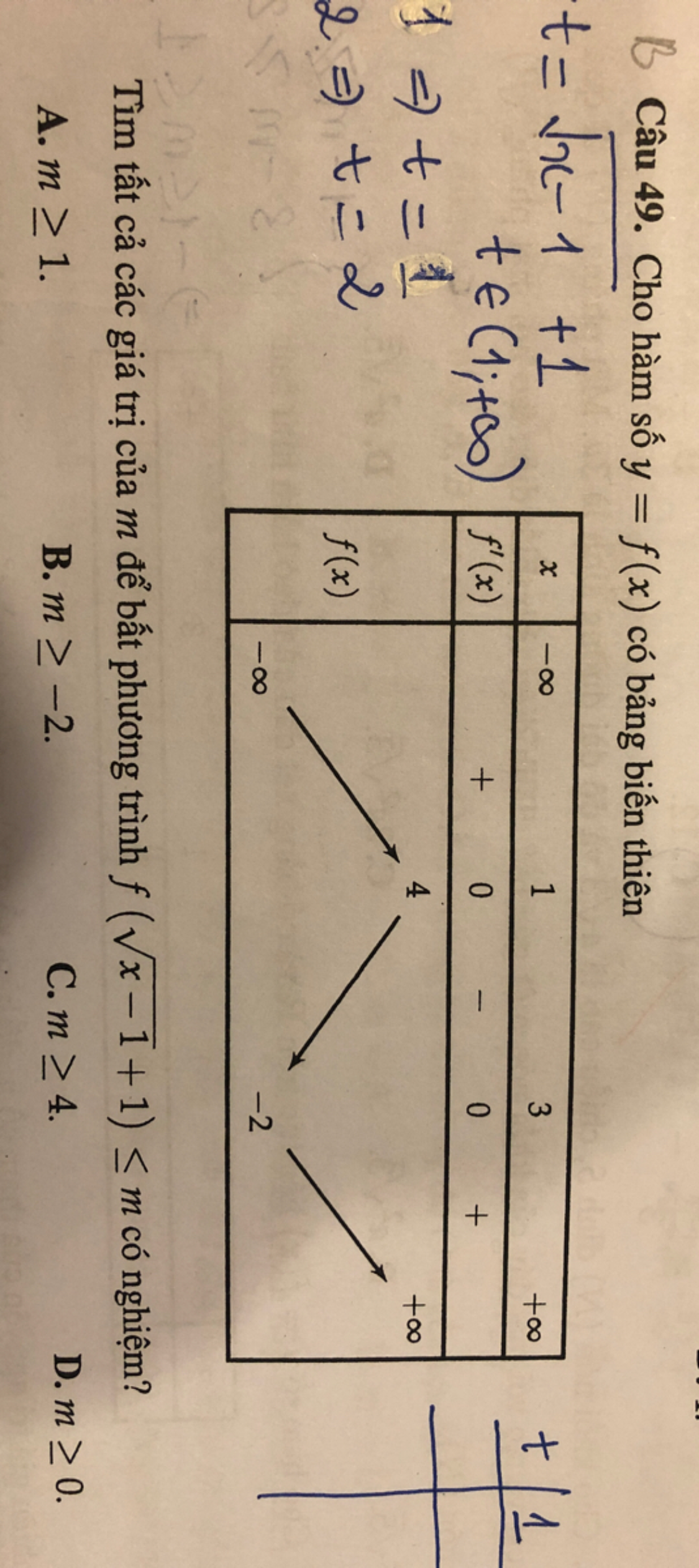 Theo dõi (1) 3 Trả lời
Theo dõi (1) 3 Trả lời -


Tìm số nghiệm của phương trình f(x^2+1)=0
bởi Bao
 22/12/2019
22/12/2019
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Đồ thị hàm số y=x^3-2x^2-x+2 có tất cả bao nhiêu giao điểm với trục hoành?
bởi Bóng Tối Hiệp Sĩ
 19/12/2019
Giao điểm
19/12/2019
Giao điểm Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm số phần tử của tập hợp S biết S là tập hợp các giá trị m để bất phương trình nghiệm đúng với mọi x thuộc R
bởi Mai Duy Trường
 19/12/2019
Câu 6
19/12/2019
Câu 6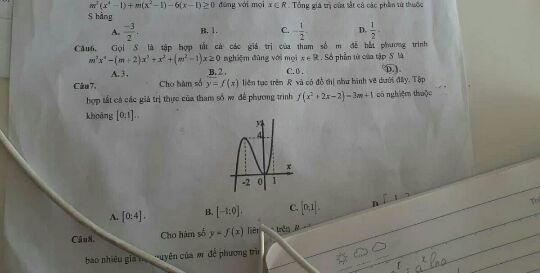 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 68 trang 61 SGK Toán 12 NC
Bài tập 69 trang 61 SGK Toán 12 NC
Bài tập 71 trang 62 SGK Toán 12 NC
Bài tập 72 trang 62 SGK Toán 12 NC
Bài tập 73 trang 62 SGK Toán 12 NC
Bài tập 74 trang 62 SGK Toán 12 NC
Bài tập 75 trang 62 SGK Toán 12 NC
Bài tập 76 trang 62 SGK Toán 12 NC
Bài tập 77 trang 62 SGK Toán 12 NC
Bài tập 78 trang 62 SGK Toán 12 NC
Bài tập 79 trang 62 SGK Toán 12 NC
Bài tập 80 trang 64 SGK Toán 12 NC
Bài tập 81 trang 64 SGK Toán 12 NC
Bài tập 82 trang 64 SGK Toán 12 NC
Bài tập 83 trang 64 SGK Toán 12 NC
Bài tập 84 trang 65 SGK Toán 12 NC
Bài tập 85 trang 65 SGK Toán 12 NC
Bài tập 86 trang 65 SGK Toán 12 NC
Bài tập 87 trang 65 SGK Toán 12 NC
Bài tập 88 trang 65 SGK Toán 12 NC
Bài tập 89 trang 65 SGK Toán 12 NC
Bài tập 90 trang 65 SGK Toán 12 NC
Bài tập 91 trang 65 SGK Toán 12 NC
Bài tập 92 trang 66 SGK Toán 12 NC
Bài tập 93 trang 66 SGK Toán 12 NC
Bài tập 94 trang 66 SGK Toán 12 NC
Bài tập 95 trang 66 SGK Toán 12 NC
Bài tập 96 trang 66 SGK Toán 12 NC
Bài tập 97 trang 67 SGK Toán 12 NC
Bài tập 98 trang 67 SGK Toán 12 NC





