Bài tập 8 trang 147 SGK Giải tích 12

Phương pháp:

Tìm GTLN, GTNN của hàm số trên miền D:

Để tìm GTLN, GTNN của hàm số \(y=f(x)\) xác định trên tập hợp D, ta tiến hành khảo sát sự biến thiên của hàm số trên D, rồi căn cứ vào bảng biến thiên của hàm số đưa ra kết luận về GTLN và GTNN của hàm số.

Tìm GTLN và GTNN của hàm số trên một đoạn:

• Định lý: Mọi hàm số liên tục trên một đoạn đều có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
•  Quy tắc tìm GTLN và GTNN của hàm số \(f(x)\) liên tục trên một đoạn \([a;b].\)
  • Tìm các điểm \(x_i\in (a ; b)\) (i = 1, 2, . . . , n) mà tại đó \(f'(x_i)=0\) hoặc \(f'(x_i)\) không xác định.
  • Tính \(f(x),f(b),f(x_i)\) (i = 1, 2, . . . , n).
  • Khi đó :  

​Lời giải:

Ta có lời giải chi tiết câu a, b, c, d bài 8:

Câu a:

\(D=\left [ -2; \frac{5}{2} \right ]\)

\(f(x) = 6x^2 - 6x - 12; f(x) = 0\Leftrightarrow \Bigg \lbrack \begin{matrix} x=-1\in D\\ \\ x=2\in D \end{matrix}\)

Ta có: \(f(-1) = 8, f(2) = -19, f(-2) =-3,f(\frac{5}{2})=-\frac{33}{2}\)

Vậy  \(\underset{x\in D}{max}f(x)=8, \underset{x\in D}{min}f(x)=-19\)

Câu b:

D = [1; e]

\(f(x) = 2x lnx +x = x(2lnx + 1)>0 \ \ \forall x\in [1;e]\)

Do đó: \(\underset{x\in D}{max}f(x)=f(e)=e^2, \underset{x\in D}{min}f(x)=f(1)=0\)

Câu c:

\(D=[0;+\infty ]\)

\(f'(x) = e^{-x} - xe^{-x} =e^{-x}(1-x)\)

\(f'(x) = 0\Leftrightarrow x=1; \lim_{x\rightarrow +\infty }f(x)=0; f(0)=0;f(1)=\frac{1}{e}\)

Bảng biến thiên

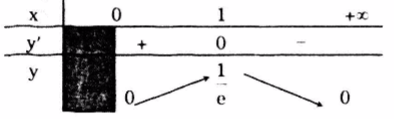
\(\underset{x \in D}{max}f(x)=f(1)=\frac{1}{e}; \underset{x \in D}{min}f(x)=f(0)=0\)

Câu d:

\(D=\left [ 0; \frac{3}{2}\pi \right ]\)

\(f'(x) = 2cosx + 2cos2x = 2(cosx + 2 cos^2x -1)\)

\(f'(x) = 0\Leftrightarrow 2cos^2x + cosx -1=0\Leftrightarrow \Bigg \lbrack \begin{matrix} cosx=-1\\ \\ cosx=\frac{1}{2} \end{matrix}\Leftrightarrow \Bigg \lbrack \begin{matrix} x= \pi\\ \\ x= \frac{\pi }{3} \end{matrix}\)

Ta có \(f(0)=f(\pi)=0, f\left ( \frac{\pi }{3} \right )=\frac{3\sqrt{3}}{2}, f\left ( \frac{3\pi }{2} \right )=-2\)

Vậy \(\underset{x\in D}{max}f(x)=f\left ( \frac{\pi }{3} \right )=\frac{3\sqrt{3}}{2}; \underset{x\in D}{min}f(x)=f\left ( \frac{3\pi }{2} \right )=-2\)

-- Mod Toán 12 HỌC247