Bài tập 2 trang 211 SGK Toán 12 NC
a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số f(x) = 2x3 – 3x2 – 12x – 10
b) Chứng minh rằng phương trình 2x3 – 3x2 – 12x – 10 = 0 có nghiệm thực duy nhất.
c) Gọi nghiệm thực duy nhất của hàm số là \(\alpha\)
Chứng ming rằng \(3,5 < \alpha < 3,6\)
Hướng dẫn giải chi tiết
a) TXD: D = R
f ’(x) = 6(x2 – x – 2)
\(f'(x) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{c}}
{x = - 1}\\
{x = 2}
\end{array}} \right.\)
Hàm số đạt cực đại tại x = 1; yCĐ = −3
Hàm số đạt cực tiểu tại x = 2;yCT = −30
\(\mathop {\lim }\limits_{x \to \pm \infty } f(x) = \pm \infty \)
Ta có bảng biến thiên:
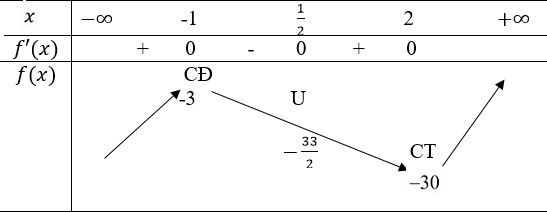
Đồ thị
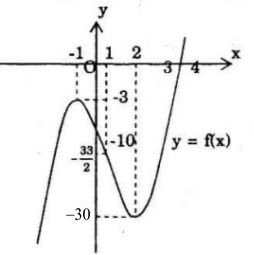
b) Đồ thị hàm số y = 2x3 – 3x2 – 12x – 10 cắt trục hoành tại một điểm duy nhất nên phương trình đã cho có nghiệm thực duy nhất.
c) Ta có: \(f(3,5).f(3,6) < 0\)
Vì vậy, phương trình có nghiệm \(\alpha\) duy nhất thỏa mãn điều kiện \(3,5 < \alpha < 3,6\).
-- Mod Toán 12 HỌC247
-


Xác định điều kiện của tham số \(m\) để đường cong \(y = {x^4} - 4m{x^2} + 3m - 2\) có ba điểm cực trị \(A,{\mkern 1mu} {\mkern 1mu} B,{\mkern 1mu} {\mkern 1mu} C\) phân biệt sao cho tam giác ABC nhận \(G\left( {0; - \dfrac{5}{3}} \right)\) làm trọng tâm?
bởi Sasu ka
 11/06/2021
11/06/2021
A. \(m = 1\) B. \(m = 1\) hoặc \(m = 0,125\)
C. \(m = 0,125\) D. \(m = 8\)
Theo dõi (0) 1 Trả lời -


Có bao nhiêu giá trị nguyên tham số \(m\) để hàm số \(y = \dfrac{{mx + 9}}{{4x + m}}\) nghịch biến trên khoảng \(\left( {0;4} \right)\)?
bởi cuc trang
 10/06/2021
10/06/2021
A. \(5\) B. 11 C. \(6\) D. \(7\)
Theo dõi (0) 1 Trả lời -


Cho biết hàm số \(y = \dfrac{{1 - x}}{{{x^2} - 2mx + 4}}\). Số giá trị thực của \(m\) để đồ thị hàm số có đúng hai đường tiệm cận ?
bởi Ha Ku
 10/06/2021
10/06/2021
A. \(2\). B. \(3\). C. \(0\). D. \(1\).
Theo dõi (0) 1 Trả lời -


Biết giá trị cực tiểu \({y_{c{\rm{r}}}}\) của hàm số \(y = {x^3} - 3{{\rm{x}}^2} + 7\) là:
bởi Lan Anh
 11/06/2021
11/06/2021
A. \({y_{c{\rm{r}}}} = 2\)
B. \({y_{c{\rm{r}}}} = 3\).
C. \({y_{c{\rm{r}}}} = 0.\)
D. \({y_{c{\rm{r}}}} = 7\).
Theo dõi (0) 1 Trả lời -


Gọi \(M,{\mkern 1mu} {\mkern 1mu} m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = \dfrac{{{x^2} + x + 3}}{{x - 2}}\) trên \(\left[ { - 2;{\mkern 1mu} {\mkern 1mu} 1} \right].\) Khi đó giá trị của \(M + m\) bằng:
bởi bala bala
 10/06/2021
10/06/2021
A. \( - 5\)
B. \( - \dfrac{9}{4}\)
C. \( - 6\)
D. \( - \dfrac{{25}}{4}\)
Theo dõi (0) 1 Trả lời -


Biết rằng hàm số \(y = f\left( x \right) = a{x^4} + b{x^2} + c\) có đồ thị là đường cong như hình vẽ bên dưới. Giá trị \(f\left( {3a + 2b + c} \right)\) là:
bởi Huong Duong
 11/06/2021
11/06/2021
.jpg)
A. \(f\left( {3a + 2b + c} \right) = {\rm{\;}} - 1\) B. \(f\left( {3a + 2b + c} \right) = {\rm{\;}} - 144\)
C. \(f\left( {3a + 2b + c} \right) = {\rm{\;}} - 113\) D. \(f\left( {3a + 2b + c} \right) = 1\)
Theo dõi (0) 1 Trả lời -


Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ { - 1} \right\}\), liên tục trên mỗi khoảng xác định và có bảng biến thiên. Khẳng định nào dưới đây là đúng?
bởi Vũ Hải Yến
 10/06/2021
10/06/2021
.jpg)
A. Đồ thị hàm số đã cho có hai tiệm cận ngang
B. Hàm số đạt cực đại tại \(x = 2\).
C. Giá trị lớn nhất của hàm số là 3
D. Đồ thị hàm số không có tiệm cận đứng
Theo dõi (0) 1 Trả lời -


Trong các hàm số bên dưới, hàm số nào nghịch biến trên khoảng \(\left( {0;\sqrt 2 } \right)\)?
bởi Nguyen Phuc
 11/06/2021
11/06/2021
A. \(y = \dfrac{{{x^2} + x - 1}}{{x - 1}}\) B. \(y = \dfrac{{2x - 5}}{{x + 1}}\)
C. \(y = \dfrac{1}{2}{x^4} - 2{x^2} + 3\) D. \(y = \dfrac{3}{2}{x^3} - 4{x^2} + 6x + 9\)
Theo dõi (0) 1 Trả lời -


Có số giá trị nguyên của tham số \(m\) để hàm số \(y = {\rm{\;}} - \dfrac{1}{3}{x^3} + m{x^2} - \left( {3 + 2m} \right)x - 2020\) nghịch biến trên \(\mathbb{R}\) là:
bởi thanh duy
 11/06/2021
11/06/2021
A. 5 B. 4 C. 2 D. 3
Theo dõi (0) 1 Trả lời -


A. \(\left( { - 1; + \infty } \right)\)
B. \(\left( { - \infty ; - 1} \right) \cup \left( {1; + \infty } \right)\)
C. \(\left( { - \infty ; - 1} \right)\)và \(\left( {1; + \infty } \right)\)
D. \(\left( { - \infty ;1} \right)\)
Theo dõi (0) 1 Trả lời -


Với hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm là \(f'\left( x \right) = {x^2}\left( {{x^2} - 4} \right)\left( {{x^2} - 3x + 2} \right)\left( {x - 3} \right)\). Hàm số có bao nhiêu điểm cực đại?
bởi Hương Lan
 11/06/2021
11/06/2021
A. \(1\) B. \(2\) C. \(0\) D. \(3\)
Theo dõi (0) 1 Trả lời -


Hàm số sau đây \(y = \dfrac{{x + 1}}{{x - 2}}\). Khẳng định nào sau đây đúng?
bởi Lê Văn Duyệt
 11/06/2021
11/06/2021
A. Hàm số đã cho nghịch biến trên từng khoảng xác định.
B. Hàm số đã cho nghịch biến trên \(\mathbb{R}\).
C. Hàm số đã cho nghịch biến trên tập \(\left( { - \infty ;2} \right) \cup \left( {2; + \infty } \right).\)
D. Hàm số đã cho đồng biến trên từng khoảng xác định.
Theo dõi (0) 1 Trả lời -


A. \(y = \dfrac{{2 - x}}{x}\). B. \(y = \dfrac{x}{{{x^2} - x + 1}}\).
C. \(y = \dfrac{1}{{{x^2} - 1}}\). D. \(y = \dfrac{{x - 1}}{{x + 1}}\).
Theo dõi (0) 1 Trả lời -


Cho hàm số \(y = \dfrac{{\sqrt {x - 2} }}{{\left( {{x^2} - 4} \right)\left( {2x - 7} \right)}}\). Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là đáp án:
bởi khanh nguyen
 11/06/2021
11/06/2021
A. \(3\) B. \(2\) C. \(5\) D. \(4\)
Theo dõi (0) 1 Trả lời -


Với hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = \left( {{x^2} - 1} \right)\left( {{x^2} - 4} \right)\left( {{x^2} + x} \right),{\mkern 1mu} {\mkern 1mu} x \in \mathbb{R}\). Hỏi hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực trị?
bởi Hoàng Anh
 11/06/2021
11/06/2021
A. \(6\) B. \(5\) C. \(3\) D. \(4\)
Theo dõi (0) 1 Trả lời -


A. \(M\left( {1; - 4} \right)\)
B. \(y = {\rm{\;}} - 4\)
C. \(x = 1\)
D. \(x = {\rm{\;}} - 1\)
Theo dõi (0) 1 Trả lời -


Cho hàm số \(y = \dfrac{{x + 1}}{{x - 1}}\). Hãy tìm phương trình tiếp tuyến với đồ thị hàm số tại điểm \(M\left( {2;3} \right).\)
bởi Nguyễn Vân
 11/06/2021
11/06/2021
A. \(y = 2x - 1\) B. \(y = {\rm{\;}} - 3x + 9\)
C. \(y = 3x - 3\) D. \(y = {\rm{\;}} - 2x + 7\)
Theo dõi (0) 1 Trả lời -


Cho biết giá trị nhỏ nhất của hàm số \(y = \sin x\) trên đoạn \(\left[ {0;\pi } \right]\) là:
bởi Xuan Xuan
 11/06/2021
11/06/2021
A. \( - 1\) B. \(\dfrac{1}{2}\) C. \(0\) D. \(1\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 16 trang 148 SGK Giải tích 12
Bài tập 1 trang 211 SGK Toán 12 NC
Bài tập 3 trang 211 SGK Toán 12 NC
Bài tập 4 trang 212 SGK Toán 12 NC
Bài tập 5 trang 212 SGK Toán 12 NC
Bài tập 6 trang 212 SGK Toán 12 NC
Bài tập 7 trang 212 SGK Toán 12 NC
Bài tập 8 trang 212 SGK Toán 12 NC
Bài tập 9 trang 212 SGK Toán 12 NC
Bài tập 11 trang 213 SGK Toán 12 NC
Bài tập 12 trang 213 SGK Toán 12 NC
Bài tập 13 trang 213 SGK Toán 12 NC
Bài tập 14 trang 213 SGK Toán 12 NC
Bài tập 15 trang 213 SGK Toán 12 NC
Bài tập 16 trang 213 SGK Toán 12 NC
Bài tập 17 trang 213 SGK Toán 12 NC
Bài tập 18 trang 214 SGK Toán 12 NC
Bài tập 19 trang 214 SGK Toán 12 NC
Bài tập 20 trang 214 SGK Toán 12 NC
Bài tập 21 trang 214 SGK Toán 12 NC
Bài tập 22 trang 214 SGK Toán 12 NC
Bài tập 23 trang 214 SGK Toán 12 NC
Bài tập 24 trang 214 SGK Toán 12 NC
Bài tập 25 trang 215 SGK Toán 12 NC
Bài tập 26 trang 214 SGK Toán 12 NC
Bài tập 27 trang 215 SGK Toán 12 NC
Bài tập 28 trang 215 SGK Toán 12 NC
Bài tập 29 trang 215 SGK Toán 12 NC
Bài tập 30 trang 215 SGK Toán 12 NC
Bài tập 31 trang 216 SGK Toán 12 NC
Bài tập 32 trang 216 SGK Toán 12 NC
Bài tập 33 trang 216 SGK Toán 12 NC
Bài tập 34 trang 216 SGK Toán 12 NC
Bài tập 35 trang 216 SGK Toán 12 NC
Bài tập 36 trang 217 SGK Toán 12 NC
Bài tập 37 trang 217 SGK Toán 12 NC
Bài tập 38 trang 217 SGK Toán 12 NC
Bài tập 1 trang 216 SBT Toán 12
Bài tập 2 trang 216 SBT Toán 12
Bài tập 3 trang 216 SBT Toán 12
Bài tập 4 trang 216 SBT Toán 12
Bài tập 5 trang 216 SBT Toán 12
Bài tập 6 trang 216 SBT Toán 12
Bài tập 7 trang 216 SBT Toán 12
Bài tập 8 trang 217 SBT Toán 12
Bài tập 9 trang 217 SBT Toán 12
Bài tập 10 trang 217 SBT Toán 12
Bài tập 11 trang 217 SBT Toán 12
Bài tập 12 trang 218 SBT Toán 12
Bài tập 13 trang 218 SBT Toán 12
Bài tập 14 trang 218 SBT Toán 12
Bài tập 15 trang 218 SBT Toán 12
Bài tập 16 trang 218 SBT Toán 12
Bài tập 17 trang 218 SBT Toán 12
Bài tập 18 trang 219 SBT Toán 12
Bài tập 19 trang 219 SBT Toán 12
Bài tập 20 trang 219 SBT Toán 12
Bài tập 21 trang 219 SBT Toán 12
Bài tập 22 trang 219 SBT Toán 12
Bài tập 23 trang 220 SBT Toán 12
Bài tập 24 trang 220 SBT Toán 12
Bài tập 25 trang 220 SBT Toán 12





