Bài tập 3 trang 216 SBT Toán 12
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số : \(y = {{4x - 5} \over {x - 1}}\)
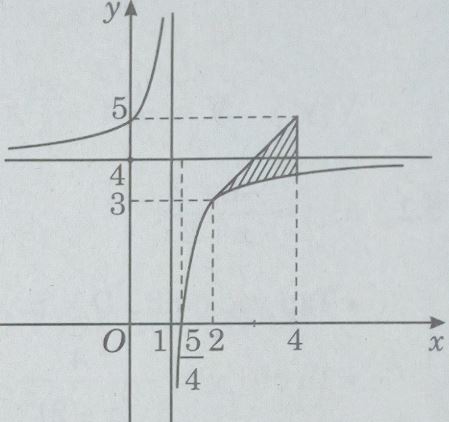
b) Tính diện tích hình phẳng giới hạn bởi (C), tiếp tuyến của (C) tại A(2; 3) và đường thẳng x = 4.
Hướng dẫn giải chi tiết Bài tập 3 trang 216
a) Tập xác định: D = R\{1}
Đạo hàm: \(y' = {1 \over {{{(x - 1)}^2}}}\)
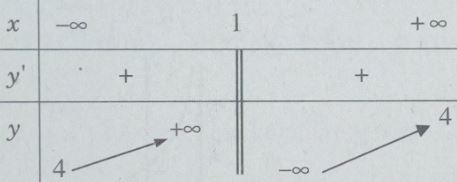
Bảng biến thiên:
Các khoảng đồng biến là \(( - \infty ;1)\) và \((1; + \infty )\) :
Tiệm cận đứng x = 1 vì \(\mathop {\lim }\limits_{x \to {1^ + }} y = - \infty ;\mathop {\lim }\limits_{x \to {1^ - }} y = + \infty \)
Tiệm cận ngang y = 4 vì \(\mathop {\lim }\limits_{x \to \pm \infty } y = 4\)
Giao với các trục tọa độ: (0; 5) và \(({5 \over 4};0)\)
Đồ thị
b) Ta có: y’(2) = 1. Phương trình tiếp tuyến là \(y = 1\left( {x - 2} \right) + 3 \Leftrightarrow y = x + 1\)
Diện tích của miền cần tìm là:
\(S = \int\limits_2^4 {\left( {x + 1 - \dfrac{{4x - 5}}{{x - 1}}} \right)dx} \) \( = \int\limits_2^4 {\left( {x + 1 - 4 + \dfrac{1}{{x - 1}}} \right)dx} \)\( = \int\limits_2^4 {\left( {x - 3 + \dfrac{1}{{x - 1}}} \right)dx} \) \( = \left. {\left( {\dfrac{{{x^2}}}{2} - 3x + \ln \left| {x - 1} \right|} \right)} \right|_2^4\) \( = - 4 + \ln 3 + 4 = \ln 3\)
-- Mod Toán 12 HỌC247
-


Tổng độ dài \(l\) tất cả các cạnh của khối mười hai mặt đều có cạnh bằng 2 là bằng bao nhiêu?
bởi Phung Thuy
 07/06/2021
07/06/2021
A. \(l = 60\)
B. \(l = 16\)
C. \(l = 24\)
D. \(l = 8\)
Theo dõi (0) 1 Trả lời -


Hãy tìm tất cả các giá trị thực của \(m\) để đường thẳng \(d:y = mx + 2\) cắt đồ thị \(\left( C \right):y = \dfrac{{x + 1}}{x}\) tại 2 điểm thuộc 2 nhánh của đồ thị \(\left( C \right)\)
bởi Hoàng Anh
 06/06/2021
06/06/2021
A. \(m \le 0\)
B. \(m > \dfrac{1}{2}\)
C. \(m \le 1\)
D. \(m > 0\)
Theo dõi (0) 1 Trả lời -


Cho hàm số sau \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị là đường cong trong hình dưới đây. Khẳng định nào sau đây đúng?
bởi ngọc trang
 06/06/2021
06/06/2021
.png)
A. \(a < 0,c < 0,d > 0\)
B. \(a < 0,c < 0,d < 0\)
C. \(a > 0,c > 0,d > 0\)
D. \(a < 0,c > 0,d > 0\)
Theo dõi (0) 1 Trả lời -


Cho hình nón có chiều cao bằng 4 và bán kính đáy bằng 3. Cắt hình nón đã cho bởi mặt phẳng đi qua đỉnh và cách tâm của đáy một khoảng bằng 2, ta được thiết diện có diện tích bằng đáp án?
bởi Nguyen Dat
 07/06/2021
07/06/2021
A. \(20\)
B. \(10\)
C. \(\dfrac{{16\sqrt {11} }}{3}\)
D. \(\dfrac{{8\sqrt {11} }}{3}\)
Theo dõi (0) 1 Trả lời -


Tìm giá trị \(m\) để hàm số \(f\left( x \right) = \left( {m + 2} \right)\dfrac{{{x^3}}}{3} - \left( {m + 2} \right){x^2} + \left( {m - 8} \right)x + {m^2} - 1\) nghịch biến trên \(\mathbb{R}\)
bởi Nguyễn Minh Hải
 07/06/2021
07/06/2021
A. \(m \ge - 2\)
B. \(m < - 2\)
C. \(m \in \mathbb{R}\)
D. \(m \le - 2\)
Theo dõi (0) 1 Trả lời -


Một chất điểm chuyển động theo quy luật \(S = 6{t^2} - {t^3}\). Vận tốc \(v\left( {m/s} \right)\) của chất điểm đạt giấ trị lớn nhất tại thới điểm \(t\left( s \right)\) bằng đáp án?
bởi Nguyễn Lê Thảo Trang
 07/06/2021
07/06/2021
A. \(2\left( s \right)\)
B. \(12\left( s \right)\)
C. \(6\left( s \right)\)
D. \(4\left( s \right)\)
Theo dõi (0) 1 Trả lời -


Một doanh nghiệp sản xuất và bán một loại sản phẩm với giá 45 (ngàn đồng) mỗi sản phẩm, tại giá bán này khách hàng sẽ mua 60 sản phẩm mỗi tháng. Doanh nghiệp dự định tăng giá bạn và họ ước tính rằng nếu tăng 2 (ngàn đồng) trong giá bán thì mỗi tháng sẽ bán ít hơn 6 sản phẩm. Biết rằng chi phí sản xuất mỗi sản phẩm là 27 (ngàn đồng). Cho biết doanh nghiệp nên bán sản phẩm với giá nào để lợi nhuận thu được lớn nhất?
bởi A La
 07/06/2021
07/06/2021
A. 47 ngàn đồng
B. 46 ngàn đồng
C. 48 ngàn đồng
D. 49 ngàn đồng
Theo dõi (0) 1 Trả lời -


Các hàm số \(y = {a^x}\) và \(y = {b^x}\) với \(a,b\) là những số thực dương khác 1 có đồ thị như hình vẽ. Đường thẳng \(y = 3\) cắt trục tung, đồ thị hàm số \(y = {a^x}\) và \(y = {b^x}\) lần lượt tại \(H,M,N\). Biết rằng \(2HM = 3MN\), khẳng định nào sau đây đúng?
bởi Ban Mai
 07/06/2021
07/06/2021
.png)
A. \({a^5} = {b^3}\)
B. \(3a = 5b\)
C. \({a^3} = {b^5}\)
D. \({a^2} = {b^3}\)
Theo dõi (0) 1 Trả lời -


Cho \({\log _2}x = 6{\log _4}a - 4{\log _2}\sqrt b - {\log _{\dfrac{1}{2}}}c\), với \(a,b,c\) là các số thực dương bất kì. Khẳng định nào sau đây đúng?
bởi Huong Giang
 06/06/2021
06/06/2021
A. \(x = \dfrac{{{a^3}}}{{{b^2}c}}\)
B. \(x = \dfrac{{{a^3}c}}{{{b^2}}}\)
C. \(x = {a^3} - {b^2} + c\)
D. \(x = \dfrac{{a{c^3}}}{{{b^2}}}\)
Theo dõi (0) 1 Trả lời -


Tập xác định \(D\) của hàm số \(y = {\left( {x - 2} \right)^{\sqrt 2 }}\) là đáp án?
bởi Kim Ngan
 07/06/2021
07/06/2021
A. \(D = \left( {2; + \infty } \right)\)
B. \(D = \mathbb{R}\)
C. \(D = \left( { - \infty ;2} \right)\)
D. \(D = \mathbb{R}\backslash \left\{ 2 \right\}\)
Theo dõi (0) 1 Trả lời -


Cho biết tập xác định \(D\) của hàm số \(y = {\log _3}\left( {{{\log }_2}x} \right)\) là
bởi Phan Thiện Hải
 07/06/2021
07/06/2021
A. \(D = \mathbb{R}\)
B. \(D = \left( {0;1} \right)\)
C. \(D = \left( {0; + \infty } \right)\)
D. \(D = \left( {1; + \infty } \right)\)
Theo dõi (0) 1 Trả lời -


Với \(a,b\) là hai số thực dương và \(a \ne 1\), \({\log _{\sqrt a }}\left( {a\sqrt b } \right)\) bằng đáp án?
bởi Anh Nguyễn
 06/06/2021
06/06/2021
A. \(2 + {\log _a}b\)
B. \(\dfrac{1}{2} + \dfrac{1}{2}{\log _a}b\)
C. \(2 + 2{\log _a}b\)
D. \(\dfrac{1}{2} + {\log _a}b\)
Theo dõi (0) 1 Trả lời -


Với \({\log _{\dfrac{1}{2}}}\left( {\dfrac{1}{5}} \right) = a\). Phương án nào dưới đây đúng?
bởi My Hien
 07/06/2021
07/06/2021
A. \({\log _2}5 = - a\)
B. \({\log _2}25 + {\log _2}\sqrt 5 = \dfrac{{5a}}{2}\)
C. \({\log _5}4 = - \dfrac{2}{a}\)
D. \({\log _2}\dfrac{1}{5} + {\log _2}\dfrac{1}{{25}} = 3a\)
Theo dõi (0) 1 Trả lời -


Tiệm cận đứng của đồ thị hàm số sau \(y = \dfrac{{x - 1}}{{x + 1}}\) là đường thẳng có phương trình:
bởi Bánh Mì
 07/06/2021
07/06/2021
A. \(y = - 1\)
B. \(x = - 1\)
C. \(y = 1\)
D. \(x = 1\)
Theo dõi (0) 1 Trả lời -


Hàm số \(y = f\left( x \right)\) có đạo hàm là \(f'\left( x \right) = {x^2}{\left( {x + 1} \right)^3}\left( {2 - 3x} \right)\). Số điểm cực trị của hàm số \(f\left( x \right)\) là bằng bao nhiêu?
bởi can chu
 07/06/2021
07/06/2021
A. \(0\)
B. \(2\)
C.\(3\)
D. \(1\)
Theo dõi (0) 1 Trả lời -


Hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau: Phương án nào dưới đây là đúng?
bởi thanh hằng
 07/06/2021
07/06/2021
.png)
A. Hàm số nghịch biến trên \(\mathbb{R}\)
B. Hàm số nghịch biến trên \(\mathbb{R}\backslash \left\{ 2 \right\}\)
C. Hàm số nghịch biến trên \(\left( { - \infty ;2} \right);\left( {2; + \infty } \right)\)
D. Hàm số đồng biến trên \(\left( { - \infty ;2} \right);\left( {2; + \infty } \right)\)
Theo dõi (0) 1 Trả lời -


Cho hàm số sau \(y = f\left( x \right)\) có đồ thị là đường cong trong hình dưới đây. Tìm số nghiệm thực của phương trình \(f\left( x \right) = 1\).
bởi Nguyễn Phương Khanh
 07/06/2021
07/06/2021
.png)
A. \(2\)
B. \(3\)
C. \(1\)
D. \(0\)
Theo dõi (0) 1 Trả lời -


A. \(\left( {2;0} \right)\)
B. \(\left( {0;2} \right)\)
C. \(\left( { - 2;6} \right)\)
D. \(\left( { - 2; - 18} \right)\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 1 trang 216 SBT Toán 12
Bài tập 2 trang 216 SBT Toán 12
Bài tập 4 trang 216 SBT Toán 12
Bài tập 5 trang 216 SBT Toán 12
Bài tập 6 trang 216 SBT Toán 12
Bài tập 7 trang 216 SBT Toán 12
Bài tập 8 trang 217 SBT Toán 12
Bài tập 9 trang 217 SBT Toán 12
Bài tập 10 trang 217 SBT Toán 12
Bài tập 11 trang 217 SBT Toán 12
Bài tập 12 trang 218 SBT Toán 12
Bài tập 13 trang 218 SBT Toán 12
Bài tập 14 trang 218 SBT Toán 12
Bài tập 15 trang 218 SBT Toán 12
Bài tập 16 trang 218 SBT Toán 12
Bài tập 17 trang 218 SBT Toán 12
Bài tập 18 trang 219 SBT Toán 12
Bài tập 19 trang 219 SBT Toán 12
Bài tập 20 trang 219 SBT Toán 12
Bài tập 21 trang 219 SBT Toán 12
Bài tập 22 trang 219 SBT Toán 12
Bài tập 23 trang 220 SBT Toán 12
Bài tập 24 trang 220 SBT Toán 12
Bài tập 25 trang 220 SBT Toán 12