Bài tập 9 trang 212 SGK Toán 12 NC
a) Vẽ đồ thị của các hàm số y = 2x; \(y = {(\sqrt 2 )^x}\) và \(y = {(\sqrt 3 )^x}\) trên cùng một mặt phẳng tọa độ,
Hãy nêu nhận xét về trị trí tương đối của ba đồ thị hàm số đó.
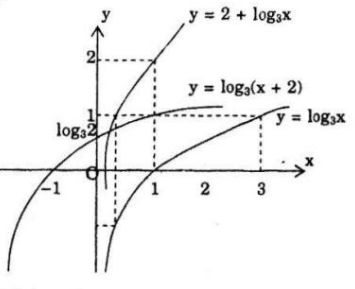
b) Vẽ đồ thị hàm số y = log3x.
Từ đó suy ra đồ thị của hàm số y = 2 + log3x và đồ thị của hàm số y = log3(x + 2)
Hướng dẫn giải chi tiết
a) Với x > 0 thì \({2^x} > {(\sqrt 3 )^x} > {(\sqrt 2 )^x}\)
nên x > 0 đồ thị y = 2x nằm phía trên đồ thị \(y = {(\sqrt 3 )^x}\) và đồ thị \(y = {(\sqrt 3 )^x}\) nằm phía trên đồ thị \(y = {(\sqrt 2 )^x}\)
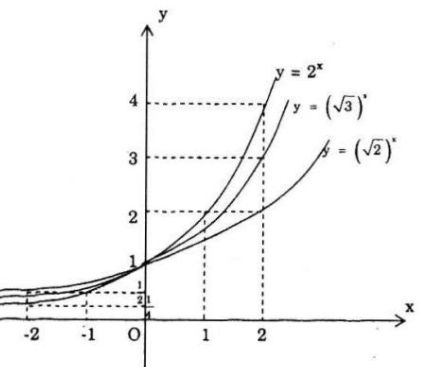
Với x < 0 thì \({2^x} < {(\sqrt 3 )^x} < {(\sqrt 2 )^x}\)
nên với x < 0 thì y = 2x nằm phía dưới đồ thị \(y = {(\sqrt 3 )^x}\) và đồ thị \(y = {(\sqrt 3 )^x}\) nằm phía dưới đồ thị \(y = {(\sqrt 2 )^x}\)
b) Đồ thị y = 2 + log3x có được bằng cách tịnh tiến lên 2 đơn vị của đồ thị y = log3x
Đồ thị y = log3(x + 2) có được bằng cách tịnh tiến sang trái 2 đơn vị của đồ thị y = log3x
-- Mod Toán 12 HỌC247
-


A. \({\log _b}c = \frac{{{{\log }_a}c}}{{{{\log }_a}b}}\).
B. \({\log _a}\left( {bc} \right) = {\log _a}b + {\log _a}c\).
C. \({\log _a}\frac{b}{c} = {\log _a}b - {\log _a}c\).
D. \({\log _a}{b^\alpha } = \frac{1}{\alpha }{\log _a}b\).
Theo dõi (0) 1 Trả lời -


Cho biết đồ thị hàm số \(y = \frac{{x - 3}}{{{x^2} - 9}}\) có mấy đường tiệm cận
bởi Hoang Vu
 10/06/2021
10/06/2021
A. \(0\). B. \(3\).
C. \(1\). D. \(2\).
Theo dõi (0) 1 Trả lời -


Cho hàm số \(f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x{\left( {x - 1} \right)^2}{\left( {x + 4} \right)^3},\forall x \in \mathbb{R}\). Số điểm cực trị của hàm số đã cho là câu?
bởi Kim Xuyen
 10/06/2021
10/06/2021
A. \(6\). B. \(1\).
C. \(3\). D. \(2\).
Theo dõi (0) 1 Trả lời -


Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\). Gọi \(S\) là diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right),y = 0,x = - 1,x = 2\) (như hình vẽ bên). Mệnh đề nào dưới đây đúng?
bởi Nguyễn Hiền
 09/06/2021
09/06/2021
.jpg)
A. \(S = \int\limits_{ - 1}^1 {f\left( x \right){\rm{d}}x} - \int\limits_1^2 {f\left( x \right){\rm{d}}x} \).
B. \(S = \int\limits_{ - 1}^1 {f\left( x \right){\rm{d}}x} + \int\limits_1^2 {f\left( x \right){\rm{d}}x} \).
C. \(S = \int\limits_{ - 1}^2 {f\left( x \right){\rm{d}}x} \).
D. \(S = - \int\limits_{ - 1}^2 {f\left( x \right){\rm{d}}x} \).
Theo dõi (0) 1 Trả lời -


A. \(3 + 4i\). B. \(3 - 4i\).
C. \(4 - 3i\). D. \(4 + 3i\).
Theo dõi (0) 1 Trả lời -


A. \(x = - 3\). B. \(x = - 4\).
C. \(x = 3\). D. \(x = 5\).
Theo dõi (0) 1 Trả lời -


A. \(y' = \frac{1}{{\left( {3x + 1} \right)\ln 2}}\)
B. \(y' = \frac{3}{{3x + 1}}\)
C. \(y' = \frac{1}{{3x + 1}}\)
D. \(y' = \frac{3}{{\left( {3x + 1} \right)\ln 2}}\)
Theo dõi (0) 1 Trả lời -


Rút gọn biểu thức sau \(P = {\left( {5 - 2\sqrt 6 } \right)^{2020}}.{\left( {5 + 2\sqrt 6 } \right)^{2018}}\) được kết quả bằng
bởi Nguyen Nhan
 10/06/2021
10/06/2021
A. \(1\).
B. \(2\).
C. \(49 + 20\sqrt 6 \).
D. \(49 - 20\sqrt 6 \).
Theo dõi (0) 1 Trả lời -


Cho \(f\left( x \right) = \frac{1}{{{x^2} - 4x + 5}} - \frac{{{x^2}}}{4} + x\). Gọi \(M = \mathop {Max}\limits_{x \in \left[ {0;3} \right]} f\left( x \right);m = \mathop {Min}\limits_{x \in \left[ {0;3} \right]} f\left( x \right).\) Khi đó ta có \(M-m\) bằng:
bởi Hoai Hoai
 10/06/2021
10/06/2021
A. \(1\).
B. \(\frac{3}{5}.\)
C. \(\frac{7}{5}.\)
D. \(\frac{9}{5}.\)
Theo dõi (0) 1 Trả lời -


Cho biết rằng \({x_1}\), \({x_2}\) là hai nghiệm của phương trình \({\log _7}\left( {\frac{{4{x^2} - 4x + 1}}{{2x}}} \right) + 4{x^2} + 1 = 6x\) và giả sử \(x{{\kern 1pt} _1} + 2{x_2} = \frac{1}{4}\left( {a + \sqrt b } \right)\) với \(a,\) \(b\) là hai số nguyên dương. Khi đó \(a + b\) bằng
bởi Vu Thy
 10/06/2021
10/06/2021
A. \(a + b = 14.\)
B. \(a + b = 13.\)
C. \(a + b = 16.\)
D. \(a + b = 11.\)
Theo dõi (0) 1 Trả lời -


Cho hàm số \(f\left( x \right)\) có đạo hàm liên tục trên \(\mathbb{R}\) và thỏa mãn \(f\left( x \right) > 0,\) \(\forall x \in \mathbb{R}.\) Biết \(f\left( 0 \right) = 1\) và \(\frac{{f'\left( x \right)}}{{f\left( x \right)}} = 2 - 2x.\) Tất cả các giá trị thực của tham số \(m\) để phương trình \(f\left( x \right) = m\) có hai nghiệm thực phân biệt là:
bởi Thanh Truc
 10/06/2021
10/06/2021
A. \(0 < m < e.\)
B. \(1 < m < e.\)
C. \(m > e.\)
D. \(0 < m \le 1.\)
Theo dõi (0) 1 Trả lời -


Nếu có \(\int\limits_2^3 {\frac{{x + 2}}{{2{x^2} - 3x + 1}}{\rm{d}}x = a\ln 5 + b\ln 3 + 3\ln 2} \)\(\left( {a,b \in \mathbb{Q}} \right)\) thì giá trị của \(P = 2a - b\) là
bởi Trần Phương Khanh
 10/06/2021
10/06/2021
A. \(P = 7.\)
B. \(P = - \frac{{15}}{2}.\)
C. \(P = \frac{{15}}{2}.\)
D. \(P = 1.\)
Theo dõi (0) 1 Trả lời -


Biết diện tích hình phẳng giới hạn bởi đường \(y = 4 - \left| x \right|\) và trục hoành là
bởi Nhật Duy
 10/06/2021
10/06/2021
A. \(0\). B.\(16\).
C. \(8\). D. \(4\).
Theo dõi (0) 1 Trả lời -


Cho \(f\left( x \right)\) là một hàm số có đạo hàm liên tục trên \(\mathbb{R}\) và thỏa mãn \(f\left( 1 \right) = 1\) và \(\int\limits_0^1 {f\left( t \right){\rm{dt}}} = \frac{1}{3}.\) Giá trị của tích phân \(I = \int\limits_0^{\frac{\pi }{2}} {\sin 2x.f'\left( {\sin x} \right){\rm{d}}x} \) là:
bởi Lê Nhi
 10/06/2021
10/06/2021
A. \(I = \frac{4}{3}\). B. \(I = \frac{2}{3}\).
C. \(I = \frac{1}{3}\). D. \(I = - \frac{2}{3}\).
Theo dõi (0) 1 Trả lời -


Giả sử ta có hệ thức sau \({a^2} + 4{b^2} = 5ab{\rm{ }}\left( {a,b > 0} \right).\) Hệ thức nào sau đây đúng?
bởi Naru to
 10/06/2021
10/06/2021
A. \(2{\log _3}\left( {a + 2b} \right) = {\log _3}a + {\log _3}b.\)
B. \(2{\log _3}\frac{{a + 2b}}{2} = {\log _3}a + 2{\log _3}b.\)
C. \({\log _3}\frac{{a + 2b}}{3} = 2\left( {{{\log }_3}a + {{\log }_3}b} \right).\)
D. \(2{\log _3}\frac{{a + 2b}}{3} = {\log _3}a + {\log _3}b.\)
Theo dõi (0) 1 Trả lời -


Có hàm số \(y = - {x^3} + 3x - 2\) có đồ thị \(\left( C \right).\) Phương trình tiếp tuyến của \(\left( C \right)\) tại giao điểm của \(\left( C \right)\) với trục tung là
bởi Kim Ngan
 10/06/2021
10/06/2021
A. \(y = - 3x - 2.\)
B. \(y = 2x + 1.\)
C. \(y = - 2x + 1.\)
D. \(y = 3x - 2.\)
Theo dõi (0) 1 Trả lời -


Tập hợp các điểm biểu diễn số phức \(z\) thỏa mãn \(\left| {z - i} \right| = \left| {2 - 3i - z} \right|\) là câu?
bởi Lê Gia Bảo
 10/06/2021
10/06/2021
A. Đường tròn có phương trình \({x^2} + {y^2} = 4.\)
B. Đường thẳng có phương trình \(x + 2y + 1 = 0.\)
C. Đường thẳng có phương trình \(x - 2y - 3 = 0.\)
D. Đường elip có phương trình \({x^2} + 4{y^2} = 4.\)
Theo dõi (0) 1 Trả lời -


Cho hàm số sau \(y = \left( {x - 2} \right)\left( {{x^2} + 1} \right)\) có đồ thị \(\left( C \right).\) Mệnh đề nào dưới đây đúng?
bởi Khánh An
 10/06/2021
10/06/2021
A. \(\left( C \right)\) cắt trục hoành tại một điểm.
B. \(\left( C \right)\) cắt trục hoành tại ba điểm.
C. \(\left( C \right)\) không cắt trục hoành.
D. \(\left( C \right)\) cắt trục hoành tại hai điểm.
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 7 trang 212 SGK Toán 12 NC
Bài tập 8 trang 212 SGK Toán 12 NC
Bài tập 11 trang 213 SGK Toán 12 NC
Bài tập 12 trang 213 SGK Toán 12 NC
Bài tập 13 trang 213 SGK Toán 12 NC
Bài tập 14 trang 213 SGK Toán 12 NC
Bài tập 15 trang 213 SGK Toán 12 NC
Bài tập 16 trang 213 SGK Toán 12 NC
Bài tập 17 trang 213 SGK Toán 12 NC
Bài tập 18 trang 214 SGK Toán 12 NC
Bài tập 19 trang 214 SGK Toán 12 NC
Bài tập 20 trang 214 SGK Toán 12 NC
Bài tập 21 trang 214 SGK Toán 12 NC
Bài tập 22 trang 214 SGK Toán 12 NC
Bài tập 23 trang 214 SGK Toán 12 NC
Bài tập 24 trang 214 SGK Toán 12 NC
Bài tập 25 trang 215 SGK Toán 12 NC
Bài tập 26 trang 214 SGK Toán 12 NC
Bài tập 27 trang 215 SGK Toán 12 NC
Bài tập 28 trang 215 SGK Toán 12 NC
Bài tập 29 trang 215 SGK Toán 12 NC
Bài tập 30 trang 215 SGK Toán 12 NC
Bài tập 31 trang 216 SGK Toán 12 NC
Bài tập 32 trang 216 SGK Toán 12 NC
Bài tập 33 trang 216 SGK Toán 12 NC
Bài tập 34 trang 216 SGK Toán 12 NC
Bài tập 35 trang 216 SGK Toán 12 NC
Bài tập 36 trang 217 SGK Toán 12 NC
Bài tập 37 trang 217 SGK Toán 12 NC
Bài tập 38 trang 217 SGK Toán 12 NC
Bài tập 1 trang 216 SBT Toán 12
Bài tập 2 trang 216 SBT Toán 12
Bài tập 3 trang 216 SBT Toán 12
Bài tập 4 trang 216 SBT Toán 12
Bài tập 5 trang 216 SBT Toán 12
Bài tập 6 trang 216 SBT Toán 12
Bài tập 7 trang 216 SBT Toán 12
Bài tập 8 trang 217 SBT Toán 12
Bài tập 9 trang 217 SBT Toán 12
Bài tập 10 trang 217 SBT Toán 12
Bài tập 11 trang 217 SBT Toán 12
Bài tập 12 trang 218 SBT Toán 12
Bài tập 13 trang 218 SBT Toán 12
Bài tập 14 trang 218 SBT Toán 12
Bài tập 15 trang 218 SBT Toán 12
Bài tập 16 trang 218 SBT Toán 12
Bài tập 17 trang 218 SBT Toán 12
Bài tập 18 trang 219 SBT Toán 12
Bài tập 19 trang 219 SBT Toán 12
Bài tập 20 trang 219 SBT Toán 12
Bài tập 21 trang 219 SBT Toán 12
Bài tập 22 trang 219 SBT Toán 12
Bài tập 23 trang 220 SBT Toán 12
Bài tập 24 trang 220 SBT Toán 12
Bài tập 25 trang 220 SBT Toán 12






