Bài tập 14 trang 213 SGK Toán 12 NC
Tính các tính phân sau
a) \(\int \limits_0^1 \frac{{dx}}{{{x^2} + 1}}\)
b) \(\int \limits_0^1 \frac{{dx}}{{{x^2} + x + 1}}\)
c) \(\int \limits_0^1 {x^2}{e^x}dx\)
Hướng dẫn giải chi tiết
a) Đặt \(x = \tan t \Rightarrow dx = \frac{1}{{{{\cos }^2}t}}dt\)
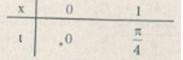
\(\int \limits_0^1 \frac{{dx}}{{{x^2} + 1}} = \int \limits_0^{\frac{\pi }{4}} \frac{{dt}}{{{{\cos }^2}t({{\tan }^2}t + 1)}} = \int \limits_0^{\frac{\pi }{4}} dt = \frac{\pi }{4}\)
b) Ta có:
\(I = \int \limits_0^1 \frac{{dx}}{{{x^2} + x + 1}} = \int \limits_0^1 \frac{{dx}}{{{{(x + \frac{1}{2})}^2} + {{(\frac{{\sqrt 3 }}{2})}^2}}}\)
Đặt \(x + \frac{1}{2} = \frac{{\sqrt 3 }}{2}\tan t\)
\( \Rightarrow dx = \frac{{\sqrt 3 }}{2}(1 + {\tan ^2}t)dt\)

\(I = \int \limits_{\frac{\pi }{6}}^{\frac{\pi }{3}} \frac{{\frac{{\sqrt 3 }}{2}dt}}{{\frac{3}{4}}} = \frac{4}{3}.\frac{{\sqrt 3 }}{2}.\frac{\pi }{6} = \frac{{\sqrt 3 \pi }}{9}\)
c) Đặt
\(\left\{ \begin{array}{l}
u = {x^2}\\
dv = {e^x}dx
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
du = 2xdx\\
v = {e^x}
\end{array} \right.\)
Do đó:
\(\begin{array}{l}
\int \limits_0^1 {x^2}{e^x}dx = {x^2}{e^x}|_0^1 - 2\int \limits_0^1 x{e^x}dx\\
= e - 2\int \limits_0^1 x{e^x}dx( * )
\end{array}\)
Đặt
\(\left\{ \begin{array}{l}
u = x\\
dv = {e^x}dx
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
du = dx\\
v = {e^x}
\end{array} \right.\)
Suy ra:
\(\int \limits_0^1 x{e^x}dx = x{e^x}|_0^1 - \int \limits_0^1 {e^x}dx = e - {e^x}|_0^1 = 1\)
Từ (*) suy ra: \(\int \limits_0^1 {x^2}{e^x}dx = e - 2\)
-- Mod Toán 12 HỌC247
-


Xác định tập nghiệm S của bất phương trình \({\log _2}\left( {2x + 3} \right) \ge 0\)là
bởi Nguyễn Thị An
 09/06/2021
09/06/2021
A. \(S = \left( { - \infty ; - 1} \right)\).
B. \(S = \left( { - \infty ; - 1} \right]\).
C. \(S = \left( { - \infty ;0} \right]\).
D. \(S = \left[ { - 1; + \infty } \right)\).
Theo dõi (0) 1 Trả lời -


Cho một hộp có \(10\) quả cầu xanh, \(5\) quả cầu đỏ. Lấy ngẫu nhiên \(5\) quả từ hộp đó. Xác suất để được \(5\) quả có đủ hai màu là
bởi Thu Hang
 09/06/2021
09/06/2021
A. \(\frac{{250}}{{273}}\). B. \(\frac{{12}}{{143}}\).
C. \(\frac{{132}}{{143}}\). D. \(\frac{{13}}{{143}}\).
Theo dõi (0) 1 Trả lời -


Tập xác định của hàm số \(y = {\log _{2020}}\left( {3x - {x^2}} \right)\) là câu
bởi hi hi
 10/06/2021
10/06/2021
A. \(D = \left( { - \infty ;\,\,0} \right) \cup \left( {3;\,\, + \infty } \right)\).
B. \(D = \left( {0;\,\, + \infty } \right)\).
C. \(D = \mathbb{R}\).
D. \(D = \left( {0;\,\,3} \right)\).
Theo dõi (0) 1 Trả lời -


Cho biết tích phân \(I = \int\limits_0^4 {x\sqrt {{x^2} + 9} {\rm{d}}x} \). Khi đặt \(t = \sqrt {{x^2} + 9} \) thì tích phân đã cho trở thành
bởi Nguyễn Tiểu Ly
 10/06/2021
10/06/2021
A. \(\int\limits_3^5 {{t^2}{\rm{d}}t} \). B. \(\int\limits_0^4 {t{\rm{d}}t} \).
C. \(\int\limits_3^5 {t{\rm{d}}t} \). D. \(\int\limits_0^4 {{t^2}{\rm{d}}t} \).
Theo dõi (0) 1 Trả lời -


A. \(5\). B. \(25\).
C. \(1\). D. \(7\).
Theo dõi (0) 1 Trả lời -


Đường tiệm cận ngang của đồ thị hàm số sau đâu \(y = {\mkern 1mu} \frac{{x - 3}}{{x - 1}}\) có phương trình là
bởi Thu Hang
 10/06/2021
10/06/2021
A. \(x = 1\).
B. \(y = 0\).
C. \(y = 5\).
D. \(y = 1\).
Theo dõi (0) 1 Trả lời -


Xác định số phức liên hợp của \(z = 4 + 3i\) là
bởi Lê Minh Bảo Bảo
 10/06/2021
10/06/2021
A. \(\overline z = 4 - 3i\).
B. \(\overline z = 3 - 4i\).
C. \(\overline z = 3 + 4i\).
D. \(\overline z = - 3 + 4i\).
Theo dõi (0) 1 Trả lời -


Với số phức sau \(z = 2 - 3i\). Điểm biểu diễn số phức liên hợp của \(z\) là
bởi Thanh Thanh
 10/06/2021
10/06/2021
A. \(\left( {2;\, - 3} \right)\).
B. \(\left( { - 2;\, - 3} \right)\).
C. \(\left( { - 2;\,3} \right)\).
D. \(\left( {2;\,3} \right)\).
Theo dõi (0) 1 Trả lời -


Tập xác định của hàm số sau đây \(y = {\left( {x - 1} \right)^{\frac{1}{5}}}\) là
bởi thu phương
 10/06/2021
10/06/2021
A. \(\left( {0; + \infty } \right)\).
B. \(\left( {1; + \infty } \right)\).
C. \(\mathbb{R}\backslash \left\{ 1 \right\}\).
D. \(\left[ {1; + \infty } \right)\).
Theo dõi (0) 1 Trả lời -


A. \(F\left( x \right) = \frac{{{x^3}}}{3} + C\).
B. \(F\left( x \right) = {x^3} + C\).
C. \(F\left( x \right) = x + C\).
D. \(F\left( x \right) = 2x + C\).
Theo dõi (0) 1 Trả lời -


Hãy tính đạo hàm của hàm số \(y = {2^x}\).
bởi Nguyễn Lê Tín
 10/06/2021
10/06/2021
A. \(y' = x{.2^{x - 1}}\ln 2\).
B. \(y' = {2^x}\ln 2\).
C. \(y' = \frac{{{2^x}}}{{\ln 2}}\).
D. \(y' = x{.2^{x - 1}}\).
Theo dõi (0) 1 Trả lời -


Vowis hàm số \(y = f\left( x \right)\) có đạo hàm \(f'\left( x \right) = x{\left( {x + 3} \right)^2}{\left( {x - 2} \right)^3},\forall x \in \mathbb{R}\). Số điểm cực trị của hàm số là:
bởi Đào Thị Nhàn
 09/06/2021
09/06/2021
A. \(1\). B. \(4\).
C. \(2\). D. \(3\).
Theo dõi (0) 1 Trả lời -


Với cấp số cộng \(\left( {{u_n}} \right)\) có \({u_1} = 3,\,{u_3} = 11\). Công sai \(d\) bằng
bởi Phạm Khánh Linh
 10/06/2021
10/06/2021
A. \(7\). B. \(2\).
C. \(3\). D. \(4\).
Theo dõi (0) 1 Trả lời -


Cho biết đồ thị của hàm số \(y = - {x^4} - 3{x^2} + 1\) cắt trục tung tại điểm có tung độ bao nhiêu
bởi Nguyễn Tiểu Ly
 09/06/2021
09/06/2021
A. 0. B. 1.
C. -1. D. -3.
Theo dõi (0) 1 Trả lời -


A. \(I = 2\).
B. \(I = \frac{1}{2}\).
C. \(I = - \frac{1}{2}\).
D. \(I = - 2\).
Theo dõi (0) 1 Trả lời -


Rút gọn biểu thức sau \(P = {x^{\frac{1}{2}}}.\sqrt[8]{x}\) (với \(x > 0\)).
bởi Nguyễn Minh Minh
 10/06/2021
10/06/2021
A. \({x^{\frac{5}{8}}}\).
B. \({x^{\frac{1}{{16}}}}\).
C. \({x^4}\).
D. \({x^{\frac{5}{{16}}}}\).
Theo dõi (0) 1 Trả lời -


Giá trị nhỏ nhất của hàm số sau \(y = \frac{{x - 1}}{{2x + 1}}\) trên đoạn \(\left[ {1;2} \right]\) là
bởi Lê Trung Phuong
 10/06/2021
10/06/2021
A. \(\frac{2}{3}\). B. \( - 2\).
C. \(\frac{1}{5}\). D. \(0\).
Theo dõi (0) 1 Trả lời -


A. \(I = 6\). B. \(I = 4\).
C. \(I = 2\). D. \(I = 5\).
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 12 trang 213 SGK Toán 12 NC
Bài tập 13 trang 213 SGK Toán 12 NC
Bài tập 15 trang 213 SGK Toán 12 NC
Bài tập 16 trang 213 SGK Toán 12 NC
Bài tập 17 trang 213 SGK Toán 12 NC
Bài tập 18 trang 214 SGK Toán 12 NC
Bài tập 19 trang 214 SGK Toán 12 NC
Bài tập 20 trang 214 SGK Toán 12 NC
Bài tập 21 trang 214 SGK Toán 12 NC
Bài tập 22 trang 214 SGK Toán 12 NC
Bài tập 23 trang 214 SGK Toán 12 NC
Bài tập 24 trang 214 SGK Toán 12 NC
Bài tập 25 trang 215 SGK Toán 12 NC
Bài tập 26 trang 214 SGK Toán 12 NC
Bài tập 27 trang 215 SGK Toán 12 NC
Bài tập 28 trang 215 SGK Toán 12 NC
Bài tập 29 trang 215 SGK Toán 12 NC
Bài tập 30 trang 215 SGK Toán 12 NC
Bài tập 31 trang 216 SGK Toán 12 NC
Bài tập 32 trang 216 SGK Toán 12 NC
Bài tập 33 trang 216 SGK Toán 12 NC
Bài tập 34 trang 216 SGK Toán 12 NC
Bài tập 35 trang 216 SGK Toán 12 NC
Bài tập 36 trang 217 SGK Toán 12 NC
Bài tập 37 trang 217 SGK Toán 12 NC
Bài tập 38 trang 217 SGK Toán 12 NC
Bài tập 1 trang 216 SBT Toán 12
Bài tập 2 trang 216 SBT Toán 12
Bài tập 3 trang 216 SBT Toán 12
Bài tập 4 trang 216 SBT Toán 12
Bài tập 5 trang 216 SBT Toán 12
Bài tập 6 trang 216 SBT Toán 12
Bài tập 7 trang 216 SBT Toán 12
Bài tập 8 trang 217 SBT Toán 12
Bài tập 9 trang 217 SBT Toán 12
Bài tập 10 trang 217 SBT Toán 12
Bài tập 11 trang 217 SBT Toán 12
Bài tập 12 trang 218 SBT Toán 12
Bài tập 13 trang 218 SBT Toán 12
Bài tập 14 trang 218 SBT Toán 12
Bài tập 15 trang 218 SBT Toán 12
Bài tập 16 trang 218 SBT Toán 12
Bài tập 17 trang 218 SBT Toán 12
Bài tập 18 trang 219 SBT Toán 12
Bài tập 19 trang 219 SBT Toán 12
Bài tập 20 trang 219 SBT Toán 12
Bài tập 21 trang 219 SBT Toán 12
Bài tập 22 trang 219 SBT Toán 12
Bài tập 23 trang 220 SBT Toán 12
Bài tập 24 trang 220 SBT Toán 12
Bài tập 25 trang 220 SBT Toán 12





