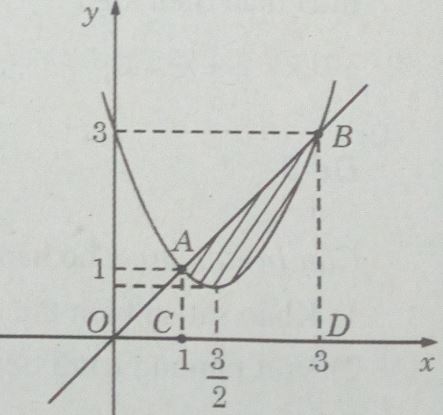Bài tập 1 trang 216 SBT Toán 12
a) Xác định a, b, c, d để đồ thị của các hàm số: y = x2 + ax + b và y = cx + d cùng đi qua hai điểm M(1; 1) và B(3; 3).
b) Vẽ đồ thị của các hàm số ứng với các giá trị a, b, c và d tìm được trên cùng một mặt phẳng tọa độ. Tính diện tích của hình phẳng giới hạn bởi hai đường cong trên.
c) Tính thể tích của vật thể tròn xoay sinh bởi hình phẳng trên quay quanh trục hoành.
Hướng dẫn giải chi tiết Bài tập 1 trang 216
a) a và b thỏa mãn hệ phương trình :
\(\left\{ {\matrix{{1 + a + b = 1} \cr {9 + 3a + b = 3} \cr} } \right. \Leftrightarrow \left\{ {\matrix{{a + b = 0} \cr {3a + b = - 6} \cr} } \right. \Leftrightarrow\left\{ {\matrix{{a = - 3} \cr {b = 3} \cr} } \right.\)
c và d thỏa mãn hệ phương trình:
\(\left\{ {\matrix{{c + d = 1} \cr {3c + d = 3} \cr} \Leftrightarrow \left\{ {\matrix{{c = 1} \cr {d = 0} \cr} } \right.} \right.\)
b)
(H.90) Ta có hai hàm số tương ứng là: y = x2 – 3x + 3 và y = x
Vậy \(S = \int\limits_1^3 {\left[ {x - \left( {{x^2} - 3x + 3} \right)} \right]dx} \) \( = \int\limits_1^3 {\left( { - {x^2} + 4x - 3} \right)dx} \) \( = \left. {\left( { - \dfrac{{{x^3}}}{3} + 2{x^2} - 3x} \right)} \right|_1^3 \) \( = 0 - \left( { - \dfrac{4}{3}} \right) = \dfrac{4}{3}\) (đơn vị diện tích)
c) V = V1 – V2 , trong đó V1 là thể tích vật thể tròn xoay sinh ra do quay hình thang ACDB quanh trục Ox , V2 là thể tích vật thể tròn xoay sinh ra do quay hình thang cong ACDB quanh trục Ox.
Ta có:
\({V_1} = \pi \int\limits_1^3 {{x^2}dx} = \pi .\left. {\dfrac{{{x^3}}}{3}} \right|_1^3 \) \(= \pi \left( {9 - \dfrac{1}{3}} \right) = \dfrac{{26\pi }}{3}\)
\({V_2} = \pi \int\limits_1^3 {{{\left( {{x^2} - 3x + 3} \right)}^2}dx} \) \( = \pi \int\limits_1^3 {\left( {{x^4} + 9{x^2} + 9 - 6{x^3} - 18x + 6{x^2}} \right)dx} \) \( = \pi \int\limits_1^3 {\left( {{x^4} - 6{x^3} + 15{x^2} - 18x + 9} \right)dx} \) \( = \left. {\pi \left( {\dfrac{{{x^5}}}{5} - \dfrac{{6{x^4}}}{4} + \dfrac{{15{x^3}}}{3} - \dfrac{{18{x^2}}}{2} + 9x} \right)} \right|_1^3\) \( = \pi \left( {\dfrac{{81}}{{10}} - \dfrac{{37}}{{10}}} \right) = \dfrac{{22\pi }}{5}\)
Vậy \(V = {{26} \over 3}\pi - {{22} \over 5}\pi = {{64} \over {15}}\pi \) (đơn vị thể tích)
-- Mod Toán 12 HỌC247
-
Vào năm 2018 dân số Việt Nam là \(96.961.884\) người và tỉ lệ tăng dân số năm đó là \(0,98\% \). Biết rằng sự gia tăng dân số được tính theo công thức \(S = A.{e^{Nr}}\), trong đó \(A\) là dân số của năm lấy mốc tính, \(S\) là dân số sau \(N\) năm, \(r\) là tỉ lệ tăng dân số hằng năm. Với tỉ lệ tăng dân số như vậy thì ít nhất đến năm nào dân số nước ta đạt \(110\) triệu người?
bởi thi trang
08/06/2021
A. \(2031\)
B. \(2035\)
C. \(2025\)
D. \(2041\)
Theo dõi (0) 1 Trả lời -
Giá trị của \(m\) để hàm số \(y = {x^3} + 3{x^2} + mx + m\) nghịch biến trên một khoảng có độ dài không nhỏ hơn 1.
bởi My Le
07/06/2021
A. \(m < 3\)
B. \(m \ge \dfrac{9}{4}\)
C.\(m \le \dfrac{9}{4}\)
D. \(m < \dfrac{9}{4}\)
Theo dõi (0) 1 Trả lời -
Hãy tìm giá trị của \(m\) để hàm số \(y = - {x^3} + 3{x^2} + m + 1\) có giá trị nhỏ nhất trên đoạn \(\left[ { - 2;1} \right]\) bằng 4 là
bởi Hương Tràm
08/06/2021
A. \(m = 4\)
B. \(m = 1\)
C. \(m = - 17\)
D. \(m = 3\)
Theo dõi (0) 1 Trả lời -
Các hàm số lũy thừa \(y = {x^\alpha }\), \(y = {x^\beta }\) và \(y = {x^\gamma }\) có đồ thị lần lượt là (1), (2) và (3) như hình vẽ. Mệnh đề nào sau đây đúng
bởi Co Nan
07/06/2021
.png)
A. \(\alpha < \beta < \gamma \)
B. \(\gamma < \alpha < \beta \)
C. \(\alpha < \gamma < \beta \)
D. \(\gamma < \beta < \alpha \)
Theo dõi (0) 1 Trả lời -
Đạo hàm của hàm số sau \(y = {\log _2}\left( {{x^2} - 2x + 3} \right)\) là đáp án
bởi cuc trang
07/06/2021
A. \(y' = \dfrac{{x - 1}}{{\ln \left( {{x^2} - 2x + 3} \right)}}\)
B.\(y' = \dfrac{1}{{\left( {{x^2} - 2x + 3} \right)\ln 2}}\)
C. \(y' = \dfrac{{2\left( {x - 1} \right)}}{{\left( {{x^2} - 2x + 3} \right)\ln 2}}\)
D. \(y' = \dfrac{{2\left( {x - 1} \right)}}{{{x^2} - 2x + 3}}\)
Theo dõi (0) 1 Trả lời -
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ dưới đây. Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là đáp án?
bởi Dương Quá
08/06/2021
.png)
A. \(4\)
B. \(2\)
C. \(5\)
D. \(3\)
Theo dõi (0) 1 Trả lời -
Hàm số sau \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có đạo hàm \(f'\left( x \right) = \left( {x - 1} \right)\left( {x - 2} \right)\left( {x - 3} \right)\). Hàm số \(y = f\left( x \right)\) có tất cả bao nhiêu điểm cực tiểu?
bởi Anh Nguyễn
07/06/2021
A. \(1\)
B. \(2\)
C. \(3\)
D. \(0\)
Theo dõi (0) 1 Trả lời -
Với đồ thị hàm số sau \(y = \dfrac{{2x + 2}}{{{x^2} - 1}}\) có bao nhiêu đường tiệm cận?
bởi Vu Thy
07/06/2021
A. \(3\)
B. \(1\)
C. \(2\)
D. \(4\)
Theo dõi (0) 1 Trả lời -
Cho phương trình sau \(\log _{\sqrt 2 }^2x - 3{\log _2}2x + 1 = 0\). Nếu đặt \(t = {\log _2}x\) thì được phương trình:
bởi Nhật Mai
08/06/2021
A. \(2{t^2} - 3t + 2 = 0\)
B. \(\dfrac{1}{4}{t^2} - 3t + 2 = 0\)
C. \(4{t^2} - 3t - 2 = 0\)
D. \(4{t^2} + t - 2 = 0\)
Theo dõi (0) 1 Trả lời -
A. \(\left( { - 1;3} \right)\)
B. \(\left( {1;3} \right)\)
C. \(\left( { - \infty ;1} \right)\) và \(\left( {3; + \infty } \right)\)
D. \(\mathbb{R}\)
Theo dõi (0) 1 Trả lời -
Ta có \({\log _2}7 = a;{\log _3}7 = b\). Giá trị của \({\log _6}7\) tính theo \(a\) và \(b\) là
bởi Thúy Vân
08/06/2021
A. \(a + b\)
B. \(\dfrac{{a + b}}{{ab}}\)
C. \(\dfrac{1}{{a + b}}\)
D. \(\dfrac{{ab}}{{a + b}}\)
Theo dõi (0) 1 Trả lời -
Cho giá trị \(a\) là số thực dương khác số 1 và \(b\) là số thực khác 0. Mệnh đề nào sau đây sai?
bởi Lê Gia Bảo
08/06/2021
A. \({\log _a}{a^b} = b\)
B. \({\log _{\dfrac{1}{a}}}a = - 1\)
C. \({\log _a}{b^4} = 4{\log _a}b\)
D. \({a^{{{\log }_a}{b^2}}} = {b^2}\)
Theo dõi (0) 1 Trả lời -
Giả sử \(M\) và \(m\) lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = 2{x^3} + 3{x^2} - 12x + 2\) trên đoạn \(\left[ { - 1;2} \right]\). Tỉ số \(\dfrac{M}{m}\) bằng
bởi Nguyễn Vũ Khúc
08/06/2021
A. \(\dfrac{{ - 6}}{5}\)
B. \( - 3\)
C.\(\dfrac{5}{2}\)
D. \( - 2\)
Theo dõi (0) 1 Trả lời -
Với hàm số \(f\left( x \right)\) có bảng biến thiên như sau. Số nghiệm thực của phương trình \(2f\left( x \right) - 7 = 0\) là:
bởi Lê Gia Bảo
08/06/2021
.png)
A. \(2\)
B. \(4\)
C. \(3\)
D. \(0\)
Theo dõi (0) 1 Trả lời -
Với đồ thị hàm số \(y = \left( {x - 1} \right)\left( {{x^2} - 4x + 4} \right)\) có bao nhiêu điểm chung với trục \(Ox?\)
bởi ngọc trang
07/06/2021
A. \(2\)
B. \(3\)
C. \(4\)
D. \(1\)
Theo dõi (0) 1 Trả lời -
Phương trình sau \({3^{2x + 1}} - {10.3^x} + 1\) có hai nghiệm phân biệt \({x_1},{x_2}\) trong đó \({x_1} < {x_2}\). Mệnh đề nào sau đây đúng?
bởi Trần Hoàng Mai
08/06/2021
A. \({x_1} + {x_2} = 0\)
B. \({x_1} + 2{x_2} = 3\)
C. \({x_1}{x_2} = 1\)
D. \(2{x_1} - {x_2} = 3\)
Theo dõi (0) 1 Trả lời -
Tập nghiệm \(S\) của phương trình sau \({5^x} = 25\) là
bởi Bảo Lộc
08/06/2021
A. \(S = \left\{ 1 \right\}\)
B. \(S = \left\{ 2 \right\}\)
C. \(S = \left\{ 0 \right\}\)
D. \(S = \left\{ 3 \right\}\)
Theo dõi (0) 1 Trả lời -
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau. Số điểm cực trị của hàm số bằng bao nhiêu?
bởi Nguyễn Hoài Thương
07/06/2021
.png)
A. \(1\)
B. \(3\)
C. \(2\)
D. \(0\)
Theo dõi (0) 1 Trả lời
Bài tập SGK khác
Bài tập 2 trang 216 SBT Toán 12
Bài tập 3 trang 216 SBT Toán 12
Bài tập 4 trang 216 SBT Toán 12
Bài tập 5 trang 216 SBT Toán 12
Bài tập 6 trang 216 SBT Toán 12
Bài tập 7 trang 216 SBT Toán 12
Bài tập 8 trang 217 SBT Toán 12
Bài tập 9 trang 217 SBT Toán 12
Bài tập 10 trang 217 SBT Toán 12
Bài tập 11 trang 217 SBT Toán 12
Bài tập 12 trang 218 SBT Toán 12
Bài tập 13 trang 218 SBT Toán 12
Bài tập 14 trang 218 SBT Toán 12
Bài tập 15 trang 218 SBT Toán 12
Bài tập 16 trang 218 SBT Toán 12
Bài tập 17 trang 218 SBT Toán 12
Bài tập 18 trang 219 SBT Toán 12
Bài tập 19 trang 219 SBT Toán 12
Bài tập 20 trang 219 SBT Toán 12
Bài tập 21 trang 219 SBT Toán 12
Bài tập 22 trang 219 SBT Toán 12
Bài tập 23 trang 220 SBT Toán 12
Bài tập 24 trang 220 SBT Toán 12
Bài tập 25 trang 220 SBT Toán 12
