Bài tập 12 trang 147 SGK Giải tích 12

90 BT SGK

Giải bài 12 tr 147 sách GK Toán GT lớp 12

Tính các tích phân sau bằng phương pháp đổi biến số:

a) \(\int_{0}^{\frac{\pi }{24}}tan \left ( \frac{\pi }{3}-4x \right )dx\) (đặt \(u=cos\left ( \frac{\pi }{3}-4x \right )\))

b) \(\int_{\frac{\sqrt{3}}{5}}^{\frac{3}{5}}\frac{dx}{9+25x^2}\) (đặt \(x=\frac{3}{5}tant\))

c) \(\int_{0}^{\frac{\pi }{2}}sin^3xcos^4xdx\) (đặt u = cosx)

d) \(\int_{-\frac{\pi }{4}}^{\frac{\pi }{4}}\frac{\sqrt{1+tanx}}{cos^2x}dx\) (đặt \(u=\sqrt{1+tanx}\))

Hướng dẫn giải chi tiết bài 12

Nhận xét:

Đề bài đã cho sẵn cách đặt các biến để thực hiện đổi biến số.

Lưu ý: Khi tính tích phân bằng phương pháp đổi biến số cần thực hiện bước đổi cận.

Lời giải:

Lời giải chi tiết câu a, b, c, d bài 12 như sau:

Câu a:

Đặt \(u=cos\left ( \frac{\pi}{3} -4x\right )\Rightarrow du= 4sin\left ( \frac{\pi}{3} -4x \right )dx\)

\(\Rightarrow sin \left ( \frac{\pi}{3} -4x \right )dx=\frac{du}{4}\)

Đổi cận:

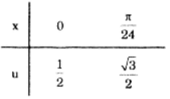
Do đó:

\(\int_{0}^{\frac{\pi }{24}}tan\left ( \frac{\pi }{3} -4x\right )dx=\int_{0}^{\frac{\pi }{24}} \frac{sin\left ( \frac{\pi }{3} -4x\right )}{cos\left ( \frac{\pi}{3}-4x \right )}dx\)

\(=\frac{1}{4}\int_{\frac{1}{2}}^{\frac{\sqrt{3} }{2}}\frac{du}{u}=\frac{1}{4}ln|u| \Bigg |_{\frac{1}{2}}^{\frac{\sqrt{3} }{2}}=\frac{1}{8}ln3\).

Câu b:

Đặt \(x=\frac{3}{5}tant\Rightarrow dx=\frac{3dt}{5cos^2t}\)

Do đó

\(\int_{\frac{\sqrt{3}}{5}}^{\frac{3}{5}}\frac{dx}{9+25x^2}= \int_{\frac{\pi }{6}}^{\frac{\pi }{4}}\frac{3dt}{5cos^2t(9+9tan^2t)}= \frac{1}{15}\int_{\frac{\pi }{6}}^{\frac{\pi }{4}}dt\)

\(=\frac{1}{15} \left ( \frac{\pi }{4}-\frac{\pi }{6} \right )=\frac{\pi }{180}\).

Câu c:

Đặt u = cosx ⇒ du = - sinx dx

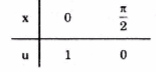
Do đó

\(\int_{0}^{\frac{\pi }{2}}sin^3xcos^4dx=\int_{1}^{0}(u^2-1)u^4du\)

\(=\int_{1}^{0}(u^6-u^4)du=\left ( \frac{u^7}{7}-\frac{u^5}{5} \right ) \Bigg |_{1}^{0}=\frac{2}{35}\).

Câu d:

Đặt \(u=\sqrt{1+tanx}\) hay \(u^2=1+tanx\Rightarrow 2udu=\frac{dx}{cos^2x}\)

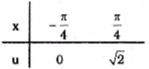
Do đó \(\int_{-\frac{\pi }{4}}^{\frac{\pi }{4}}\frac{\sqrt{1+tanx}}{cos^2x}dx= \int_{0}^{\sqrt{2}}2u^2du=\frac{2}{3}u^3 \Bigg |_{0}^{\sqrt{2}}=\frac{4\sqrt{2}}{3}\).

-- Mod Toán 12 HỌC247

Nếu bạn thấy hướng dẫn giải Bài tập 12 trang 147 SGK Giải tích 12 HAY thì click chia sẻ

YOMEDIA