Bài tập 4 trang 50 SGK Hình học 12

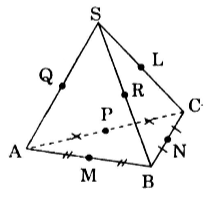
Giả sử mặt cầu (S) tiếp xúc với các cạnh SA, SB, SC tại Q, R, L và tiếp xúc với AB, BC, CA tại các trung điểm M, N, P ta có:  SQ, SR, SL là tiếp tuyến của (S) kẻ từ S nên: SQ = AM = AP = b

Tương tự, ta có: AQ = AM = AP = b

BM = BR = BN = c

CN = CP = CL = d

Mặt khác do M, N, P là trung điểm của AB = BC = CA suy ra,

AP = PC ⇒ b = d

AM = BM ⇒ b = c

⇒ AB = BC = CA = 2b = 2c = 2d

Ta có: SA = a + b, SB = a + c, SC = a + d

⇒ SA = SB = SC (2)

Từ (1) và (2) ta có S.ABC là hình chóp tam giác đều.

-- Mod Toán 12 HỌC247